Отклонения от закона Ома из-за уменьшения плотности состояний носителей в электрическом поле.

Пейсахович Ю. Г. (e-mail:ygp@nspu.nsu.ru) Новосибирский государственный педагогический университет

1 Введение.

На формирование нелинейности статической вольтамперной характеристики металлических и полупроводниковых кристаллов при больших напряжениях и токах оказывают влияние многие факторы [1]-[3],[15].

Экспериментально наблюдаемые с 1950-х годов отклонения от закона Ома в примесных полупроводниках [4] и полуметаллическом висмуте [5] описываются теорией горячих электронов [1],[2],[6]-[8]. Оценки показывают, что при реальных значениях напряженности поля F = 102 - 103 В/см и в невырожденных полупроводниках, и в сильно вырожденных металлах (висмут) требуется сравнительно малая концентрация носителей и, связанная с ней, не очень большая удельная энергия разогрева и эффективная температура электронного газа, т.е. основную роль играют припо-роговые электронные состояния в разрешенных зонах.

Полный ток обычно вычисляется с плотностью состояний неидеального кристалла без электрического поля, иначе говоря, считается, что поле не настолько сильное, чтобы заметно изменить систематику состояний статистического ансамбля, а эффект ускорения зарядов полем содержится лишь в неравновесной части функции распределения по этим состояниям.

С другой стороны, электрическое поле обязательно изменяет волновые функции и энергетическую систематику собственных состояний в ограниченной решетке: сравнительно слабо связанные электроны прижимаются к границам [1],[9], а сильно связанные образуют спектральную лестницу Ванье-Штарка [10]-[12].

Аналогичным образом электрическое поле прижимает припороговые блоховские электроны и дырки к любым статическим потенциальным барьерам, нарушающим периодичность решетки, таким, как границы кристаллитов в поликристаллах, сетка дислокаций, точечные дефекты и т.п. упругие рассеиватели, приводящие к сбою когерентной фазы блоховских волновых пакетов, и ответственные обычно за остаточное сопротивление. Эффект становится существенным, если на длине свободного пробега А между этими препятствиями носители набирают в поле F энергию eFA, сравнимую с характерной энергией в зоне (энергией Ферми £ф в металлах или тепловой квТ в полупроводниках).

Идея о том, что подобная задача о токе может быть сформулирована как кванто-вомеханическая задача о стационарных состояниях движения электрона в сложном потенциальном поле, была высказана Л.Д. Ландау в 1934 году [13],[14]. Фактически

мы имеем похожий на классический Друде-Лоренца механизм сопротивления, но с квантованием движения блоховских электронов в электрическом поле между тяжелыми препятствиями в решетке, с которыми происходят квазиупругие столкновения, что и изменяет плотность состояний. При этом механизм диссипации энергии, определяющий релаксацию, может быть любым. В частности, остаются справедливыми основные положения горячистики .

2 Ток и плотность состояний.

Рассмотрим реальный кристалл, в котором имеются статические дефекты, существенно нарушающие периодический потенциал идеальной решетки. Дефекты распределены случайно, но достаточно равномерно по объему, образуя некую сетку. При концентрации дефектов га, наиболее вероятный размер звена мезоскопической ячейки такой сетки L = га-3. Только в очень чистых и совершенных кристаллах, выращенных по специальным технологиям, L может превосходить 103 - 104 межатомных расстояний. В области масштаба меньше L решетку можно считать частью идеально периодической, условно будем называть ее кристаллитом , хотя природа дефектов может не быть поликристаллической, это могут быть и точечные примеси, причем форма искажения потенциала (кулоновская или сильно экранированная) не очень важна. В соответствии с моделью, рассмотренной в предыдущей статье [9], при включении электрического поля из состояний, близких к краям зоны Бриллюэна, происходит эффективный прижим носителей к границам кристаллитов .

Если под действием поля через образец течет стационарный ток, то воздействие поля на величину тока можно разбить на три основных фактора: а) изменение физической природы, т.е. волновых функций состояний, от размытых блоховских к стационарным состояниям в электрическом поле, учитывающим сдвиг эффективных центров зарядов электронов и дырок, изменение скоростей переноса заряда прямой и отраженной парциальными волнами, б) следующее отсюда уменьшение плотности состояний вблизи порогов зон, в) кинетическое перераспределение носителей по стационарным состояниям. В обычной теории проводимости металлов и полупроводников электрическое поле считается настолько слабым, что первыми двумя факторами можно пренебречь. Однако это не так, если ток формируется носителями из малой окрестности границ зоны Бриллюэна, состояния в которой наиболее сильно изменяются электрическим полем. Для таких состояний само понятие квазиимпульса теряет смысл в первую очередь.

Плотность тока

где к - индекс состояния с энергией £fc,Vfc - средняя скорость носителя в этом состоянии, Srik - стационарное неравновесное возмущение функции распределения ra0fc носителей в электрическом поле, в,щ - безразмерный элемент объема в простран-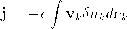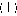

стве состояний. Все три сомножителя под интегралом (1) зависят от напряженности электрического поля F.

Скорость Vfc зависит от F наиболее слабо. В однородном электрическом поле квазиклассическое квантовое среднее значение скорости пропорциональное среднему от градиента фаз прямой и отраженной волновых экспоненциальных составляющих функций Эйри почти не зависит от поля [16], поэтому в первом приближении можно пренебречь зависимостью от F скорости волновых пакетов, переносящих ток, и считать, что вблизи порогов Vk ~ \jejra*, где е- энергия носителя, отсчитанная от порога зоны, т*- эффективная масса.

Зависимость в,щ от F обычно не учитывают. Однако, как мы показали ранее [9], ван-хововские особенности локальной энергетической плотности состояний на единицу объема кристалла Ф/е) = du/de вблизи порогов зон очень сильно зависят от электрического поля

Ф*(е) = /fc(e,F)4?0fc(e), Фок(е)

I Vfc£fc

fk(e,F)

i-£ 1EAN№ ,e>eFL

ПА(е(е|№)-1) ,e eFL

где структурные факторы /Зг- ~ /Зг- ~ 7Г, L{- размер кристаллита вдоль i- оси, произведение и сумма по i включают от нуля до трех компонент в зависимости от положения порога на границе зоны и ориентации поля F. Невозмущенная плотность состояний Ф0А:(е) дается обычным интегралом по изоэнергетической поверхности Sk в малой окрестности точки к пространства квазиимпульсов.

Добавку 8rik к функции распределения можно найти, в соответствии с теорией горячих электронов, из решения системы кинетических уравнений для электронов и фононов.

Из-за сложности, решение уравнений кинетического баланса всегда сводится к полукачественным оценкам, которые различаются для металлов и полупроводников.

3 Висмут.

В металлах основной вклад в (1) дают состояния электронов близкие к поверхности Ферми. Неомичность вольтамперной характеристики зафиксирована только у полуметаллического висмута [5] при плотности тока j = (5 -I- 10) 105 А/см2, что соответствует напряженности электрического поля Е = 10 102 В/см в интервале изменения сопротивления от гелиевых до комнатной температур. В отличие от большинства металлов, висмут имеет ферми-поверхность очень малого размера

[17] (ее объем порядка 10~5 объема зоны Бриллюэна) из-за небольшого перекрытия разрешенных зон, вызванного слабым ромбоэдрическим искажением кубической решетки. Все полости поверхности Ферми локализованы вблизи граней зоны Бриллюэна: три вытянутых электронных эллипсоида около точек L c энергией Ферми, по разным данным, £ф 3 10~2эВ и один дырочный эллипсоид около точки Т с £ф ~ 10~2эВ, что на два порядка меньше ширины зон проводимости. Это означает, что диапазон чувствительных к электрическому полю состояний (2) достигает фермиевской энергии при размерах кристаллитов L ~ бф/eF ~ 10~4 -i- 10~3 см.

Из-за уменьшения плотности состояний электрическое поле увеличивает расстояние от уровня Ферми до порога на величину ~ eFL} тем не менее, эффект прижима носителей к дефектам (2) можно грубо учесть, вводя в оценки эффективной нелинейной проводимости а в сильном поле [8] интерполирующий фактор /(еф/ \е\ FL) = /(еф, F), где к характеризует относительную часть площади ферми-поверхности б^/бф, которая значительно деформируется электрическим полем. Так, для не слишком низких температур Г, больших разогревной добавки

nesj \ Аее(Г)

1-1-/; *

el FL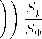

где <т0 - проводимость в слабом поле, ~ cr0F - ток, га - концентрация электронов, s -скорость звука, Хеф(Т) и Аее(Г) - длины свободного пробега между столкновениями с фононами и электронами.

Видно, что в области слабой неомичности имеется линейная по \F\ поправка, это связано с аномалией плотности состояний Ф&(£) у порога зоны, а не вблизи химического потенциала. Симметричность разогревного размытия распределения в поле относительно энергии Ферми обычно приводит к квадратичной по \F\ поправке. Е.С. Боровик [5] отмечал, что неомичность наблюдается только у отожженных образцов висмута. Отжиг благоприятствует увеличению длин свободного пробега и размера L кристаллитов , т.е. уменьшению порога неомичности по F.

4 Невырожденные полупроводники.

Изменение плотности состояний в электрическом поле может проявиться и в умеренно несовершенных кристаллах полупроводников. Нелинейность вольтамперной характеристики подробно изучалась во многих примесных полупроводниках [2]. В неполярных веществах, в зависимости от температуры, она начинается при напряженности F ~ 102 -i- 103 В/см, обычно считается, что это ниже порога генерации носителей полем. Примеси, с одной стороны, создают носителей р- или га-типа в соответствующих долинах, а с другой - обеспечивают дополнительное нарушение периодичности решетки. В большинстве классических полупроводников долины расположены на границах зоны Бриллюэна, за исключением n-Si, у которого минимумы зон проводимости смещены примерно на 0.2 расстояния от точки Х на грани

до центра зоны, однако, глубина дна зоны относительно Х всего 10~2 -I- Ю-1 эВ и может быть перекрыта напряжением eFL в электрическом поле.

Для учета уменьшения плотности состояний у порога зоны из-за прижима носителей к границам кристаллитов , как в (3), введем интерполирующий фактор f(e/ \ е\ FL) = fk(s, F) под знаком больцмановского интеграла для среднего времени релаксации при температуре разогрева носителей Те [1],[2] считая, что вся область k-пространства, дающая вклад в интеграл, соответствует прижатым состояниям, тогда

Пе- J тт(квТех)е~х x3/2f(ax)dx,a = i (4)

а

где rm(e) - время релаксации импульса носителей с энергией е при температуре Т. Вклад в г 1 от рассеяния на примесях Дт1 ~ £32 преобладает при их высокой концентрации и малой температуре Т ~ 10А , а вклад от рассеяния на фононах Дтф 1 ~ е-1/2 преобладает при малой концентрации примесей и высоких температурах. В балансе энергий, определяющем разогрев Те газа носителей электрическим полем, основную роль играют фононы. Интеграл (4) обрезается экспонентой при х ~ 1, поэтому связанное с параметром а в f(ax) уменьшение а может проявиться при L > квТе/eF. Для теплых носителей Те ~ Т (l + ([ioF/s)2J ~ Г, где /л0 - подвижность в слабом поле, что дает у пороговых напряженностей L ~ 10~4 - 10~5 см. С ростом F порог чувствительных к полю размеров L убывает. Для горячих носителей Те ~ Т (fi0F/s) ~ ЮГ, т.е. L ~ 10~5 - 10~6 см и перестает зависеть от F с ростом напряженности поля. Такие размеры областей однородности решетки соответствуют концентрации дефектов ~ L~3 ~ 1012 - 1015см~3 для теплых носителей и rid ~ 1015 - 1018см~3 для горячих. В эти диапазоны попадают концентрации примесей, которые обычно применяют при легировании [1].

5 Заключение.

Приведенные оценки показывают, что уменьшение плотности состояний вблизи порогов зон в электрическом поле может проявиться как дополнительный фактор в полевой зависимости эффективной нелинейной проводимости полуметаллов и полупроводников при условии, что проводимость определяется небольшой группой носителей, невозмущенные состояния которых лежат вблизи границ зоны Бриллюэна в области, подверженной коллапсу в электрическом поле за счет прижима их к дефектам решетки.

Список литературы

[1] Зеегер К., Физика полупроводников,М.,Мир(1977)

[2] Конуэлл Э.,Кинетические свойства полупроводников в сильных электрических полях,М.,Мир(1970)

[3] Лифшиц И.М.,Азбель М.Я.,Каганов М.И.,Электронная теория металлов.,Наука( 1971)

[4] Ryder E.J.,Schokley W., Phys. Rev.,81,139(1951)

[5] Боровик Е.С.ДАН CCCP,91,771(1953)

[6] Гинзбург В.Л.,Шабанский В.П. ДАН СССР,100,445,(1955)

[7] Шабанский В.П.,ЖЭТФ,27 ,142,147(1954);37,657(1956)

[8] Каганов М.И.Песчанский ,В.Г.,ЖЭТФ,33,1262(1956)

[9] Пейсахович Ю.Г.(пред.статья)

[10] Басе Ф.Г.,Булгаков А.А.,Тетервов А.П.,Высокочастотные свойства полупроводников со сверхрешетками.М.,Наука(1989)

[11] Wannier G.H., Elements of Solid State Theory, N.Y., Cambr. Univ.Press.(1959)

[12] Mendes E.E.,Agullo-Rueda F,HongH.M.,Phys.Rev.Lett.,60,2426(1988) Voisin P.,Blease J.,Bouche C.,et.al., Phys. Rev. Lett,61,1639(1988)

[13] Пайерлс P., Квантовая теория твердых тел,с.163,М.,ИИЛ(1956); Peierls R.,Helv.,Phys.Acta,7,Suppl.,2,24(1934)

[14] Лифшиц Е.М.,Питаевский Л.П.,Физическая кинетика,М.,Наука(1979)

[15] Басе Ф.Г.,Бочков В.С.,Гуревич Ю.Г.,Электроны и фононы в ограниченных полупроводниках,М.,Наука( 1984)

[16] Флюгге 3.,Задачи по квантовой механике,т.1,М.,Мир(1974)

[17] Эйдельман В.С,Электроны в висмуте, сб.Электроны проводимо-сти,с.229,М.,Наука(1985)