О возможности построения единой модели резонансной и релаксационной поляризации

Лукичёв А.А. (Lukichev@ascnet.ru), Ильина В.В. Институт геологии и природопользования ДВО РАН

Введение.

В современной теории поляризации сложилось устойчивое мнение, что упругие и релаксационные поляризационные процессы имеют различную физическую природу [1-6]. Теория упругой поляризации основана на модели линейного осциллятора, где заряженная частица колеблется в параболической потенциальной яме, создаваемой квазиупругой возвращающей силой. Зависимость поляризации от частоты в этом случае описывается формулами Лоренца [3]. Для описания релаксационной поляризации применяют прыжковую модель Дебая-Сканави, согласно которой релаксирующая частица находится в глубокой потенциальной яме с двумя положениями равновесия, каждое из которых частица может занять с определённой вероятностью [1,2]. Частотная зависимость описывается формулами Дебая [3]. В сложившейся ситуации существует противоречие: формулы Лоренца прямо вытекают из модели гармонического осциллятора, тогда как формулы Дебая из прыжковой модели прямо не вытекают. Это противоречие с некоторой натяжкой разрешается, обычно, тем или иным способом показывают, что существует связь между прыжковой моделью и формулами Дебая [1,5].

Отсутствие единой теории упругой и релаксационной поляризации создаёт определённые трудности в развитии теории поляризации и затрудняет понимание физической природы поляризационных процессов, это отмечал, например, Р. Коул. [7]. В то же время многие авторы обращали внимание на явное сходство дебаевских и лоренцевских зависимостей. Авторы настоящей работы считают, что единая теория упругих и релаксационных процессов может быть построена на основе модели линейного осциллятора.

Обоснование модели.

Сделаем замечание по поводу терминологии. Поскольку в этой работе предлагается описывать релаксационную поляризацию с помощью модели линейного осциллятора, основанной на понятии квазиупругой силы [3,8,9], то общепринятое деление поляризации на упругую и неупругую (релаксационную) теряет смысл. Поэтому далее мы будем использовать достаточно часто встречающееся деление на резонансную и релаксационную поляризацию.

Выделим наиболее существенные различия между резонансной и релаксационной поляризацией, для этого рассмотрим существующие определения. Определение резонансной поляризации, вытекающее из модели квазиупругой силы, достаточно очевидно и вопросов не вызывает. Но приведённые в литературе определения релаксационной поляризации следует признать неудовлетворительными. Большинство авторов определяют этот вид поляризации по признакам, которые не является достаточными. Хиппель [6] относит к релаксационной только объёмно-зарядную поляризацию и делает вывод о том, что резонансная и релаксационная поляризации имеют различную природу, поскольку последняя связана с перемещением макрозаряда в объёме диэлектрика. В работах [3,4] для определения релаксационной поляризации используется чисто качественный признак - большое время установления процесса. В [4] в качестве определения релаксационной поляризации приводится интеграл свёртки, что очевидно неверно. В [10, с.606] приведено условие трансформации формул Лоренца в формулы Дебая: а> а>0. Это неравенство отражает

известный факт, согласно которому дебаевские и лоренцевские зависимости совпадают на низких частотах [11], но признаком релаксационной поляризации не является. Все приведённые выше признаки либо недостаточны, либо просто не верны.

Единственным бесспорным признаком релаксационной поляризации является экспоненциальный спад поляризации после отключения внешнего поля:

P(t) = P,exp(-t/т) (1)

где P - поляризация, P0 - её установившееся значение в постоянном поле, т - постоянная

времени, t - время. Функция спада (1) в работах [1,4] называется функцией релаксации. Некоторые авторы в качестве функции релаксации используют функцию отклика на включение внешнего поля, что не имеет принципиальных физических отличий. Заметим, что

в электротехнике функция, подобная (1), называется переходной, это более подходящее название. Согласно определению, приведённому в [10], функция установления поляризации после ступенчатого включения (или отключения) постоянного внешнего поля для упругой поляризации имеет осцилляции в процессе установления, для релаксационной поляризации -не имеет. Очевидно, что это требование сводится к экспоненциальности функции релаксации для релаксационной поляризации, и наличия гармонических составляющих для резонансной поляризации. Последние признаки следует признать наиболее точными. Но количественных критериев они не содержат.

Таким образом, мы имеем единственный признак релаксационной поляризации (1) из которого и будем исходить при дальнейшем анализе. Далее будем считать поляризацию релаксационной, если функция релаксации диэлектрика не содержит гармонических составляющих, и резонансной, если функция релаксации содержит гармонические составляющие.

Исходим из предположения, что движение заряженной частицы в диэлектрике при наложении внешнего гармонического поля описывается уравнением для вынужденных гармонических колебаний с затуханием, как для релаксационной, так и для резонансной поляризации [3,9]:

-- + 2/?- + со 2 x = -?-0- exp(icot) (2)

dt dt m

где х - координата частицы, В - коэффициент затухания, m - масса иона, q -заряд, а>0 -

собственная частота колебаний частицы, E0 и с - амплитуда и частота изменения внешнего

поля, t - время. Для определённости считаем, что описываем движение слабосвязанного иона, участвующего в тепловой ионной поляризации. Также, считаем, что локальное поле, действующее на ион, равно среднему макроскопическому (борновское приближение [2]).

Е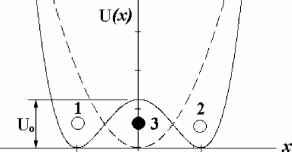

8/2

Рис. 1. потенциальной

Вид

слабосвязанного иона,

взятого иона,----для среднестатистическо- Считав

го иона.

отсутствие

внешнего

концентрация ионов в положениях 1 и 2 n1 = n2 = no / 2 , координаты положений равновесия

х12 = ±5 / 2. Очевидно, что индуцированный дипольный момент микрообъёма, содержащего

потенциальную яму, показанную на рис. 1, не равен нулю из-за асимметрии расположения заряда, в то же время момент диэлектрика в целом будет нулевым. Это означает, что поляризация всего диэлектрика определяется не положением отдельно взятого иона, а поведением центра тяжести заряда всех слабосвязанных ионов в диэлектрике. Очевидно, что при П]=п2 центр тяжести имеет координату х = 0. Таким образом, модель Сканави описывает некий усреднённый ион, координата которого совпадает с центром тяжести заряда в диэлектрике. Когда включено внешнее поле E, концентрация ионов, избыточно переброшенных в положение 2, увеличится на An, в положении 1 уменьшается на ту же величину, в этом случае центр тяжести среднестатистического иона сместится на расстояние

г л л 5 п2 - п1 An x(An) =--2-1 = 5-

2 по

Несложно заметить, что максимально возможное значение координаты х(Ап) = 5/2 достигается при Ап=п0 /2, т.е. когда все слабосвязанные ионы находятся в положении 2

в

Покажем, что модель линейного осциллятора применима для описания частицы, находящейся в потенциальной яме с двумя или более положениями равновесия. Рассмотрим движение слабосвязанного иона в глубокой потенциальной яме с двумя эквивалентными минимумами,

- разделёнными потенциальным барьером для высотой Uo, (рис. 1), при этом используем для отдельно исходные положения модели Сканави [2].

что концентрация

слабосвязанных ионов в диэлектрике равна

P(t) = р exp[- (/J2 -V/?2 02 ]t + P2 exp- (В 02 ) t (5)

где Р1 и Р2 константы, зависящие от начальных условий. Здесь мы получили переходную функцию, описывающую реакцию диэлектрика на включение внешнего поля. Как видно, эта функция отличается от (1). В случае, если

В < 0 (6)

(корни характеристического уравнения комплексные) решение (5) можно привести к виду

[8]:

P(t) = P0exp(-t /Г) sin(/ml -В2 t + <р) (7)

где Р0 - амплитуда колебаний в момент времени t = 0, Г = 1/ - постоянная времени, (р -фаза колебаний. Т.е. при выполнении условия (5) функция релаксации имеет гармонические составляющие. Если

В>ш0 (8)

(n2=n0). Смещение усреднённого иона из положения равновесия (х=0) вызовет появление возвращающей силы, обусловленной нарушением электронейтральности диэлектрика. Таким образом, если считать возвращающую силу квазиупругой, то движение среднестатистического иона с координатой х=0 может быть описано уравнением (2). Вопрос о точности такого приближения будет решён позже.

Найдём функцию отклика заряженной частицы в диэлектрике на включение внешнего поля. Используем известное выражение для дипольного момента:

p(t) = q x(t) (4)

а также его связь с поляризацией P(t) = pt (t) [1,2]. Из этих выражений следует, что

решение уравнения (2) x(t) совпадает с функцией поляризации с точностью до постоянного множителя. Отсюда несложно получить функцию отклика поляризации или функцию релаксации. Для этого ищем решение уравнения (2) с правой частью в виде E01(t), где 1(t) -единичная ступенька [12]. Частное решение такого уравнения тождественно равно константе, следовательно, о наличии гармонических составляющих в функции релаксации можно однозначно судить по виду общего решения [8]:

-г-т + т- + x = -2-°-eiat (10)

00 dx dt ma>2

Здесь введена постоянная времени:

t=24 dD

Решение уравнения (10) даёт комплексную амплитуду колебаний [3,12]:

= Щ 2, ] .-г (12)

m00 - 0 / 00 +i0т +1

Далее, с помощью соотношения (4), перейдём к индуцированному дипольному

моменту р , и, учитывая связь между моментом и поляризуемостью иона p = aE [2], из (12)

получаем комплексную поляризуемость на один ион a = a - ia :

ч q2 1 -02 /002

a(0) = --T7-- (13)

m00 (1 -02 /002 ) +02Т2

(корни характеристического уравнения действительны) то функция релаксации (5) не содержит гармонических составляющих, свободные колебания заряженной частицы становятся апериодическими. Таким образом, равенство

Р = ш0 (9)

определяет границу между гармоническим и апериодическими режимами свободных колебаний. Для вынужденных колебаний частицы под действием гармонической внешней силы апериодический режим невозможен. Пока будем считать, что равенство (9) также определяет границу между резонансным и релаксационным режимом вынужденных колебаний. Обращаем внимание, что термин вынужденные релаксационные колебания -новое понятие.

Из приведённых выражений вытекает условие существования релаксационных процессов: колебания будут релаксационными, если коэффициент затухания больше собственной частоты колебаний (выполнение неравенства (8)).

Исходя из этого, проведём анализ решения уравнения (2) с правой частью в виде гармонической функции. т.е. рассмотрим вынужденные колебания частицы под действием внешнего гармонического поля. Запишем уравнение (2) в канонической форме [12]:

а'(m)

mm02 (1 -m2/m02)2 +®2г2

В спектроскопии эти формулы известны как формулы Лоренца, графики функций для различных значений / показаны на рис. 2а и 2б. В резонансном режиме зависимость а'(m) (рис. 2а) имеет выраженный резонансный пик, при переходе через границу релаксационного режима пик исчезает, кривые выполаживаются и по форме приближаются к дебаевскому виду. Функция а (т) (рис. 2б) в резонансном режиме имеет вид узкого резонансного пика, полуширина которого равна /, амплитуда, также, существенно зависит от коэффициента затухания. В релаксационном режиме пик имеет дебаевский вид, его ширина и амплитуда от затухания уже не зависят.

Проанализируем изменение поляризуемости в зависимости от соотношения величин В и m0, для этого рассмотрим предельные случаи.

1. Затухание мало, << m0, резонансный режим колебаний.

Второй член уравнения (10), учитывающий трение, пренебрежимо мал, опускаем его, и получаем упрощенное уравнение, описывающее вырожденную колебательную систему

Из решения этого уравнения получаем формулу для поляризуемости, хорошо известную из теории электронной поляризации [3]:

[3,9]:

j ctxx

m02 dt2

+ x =

(15)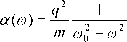

(16)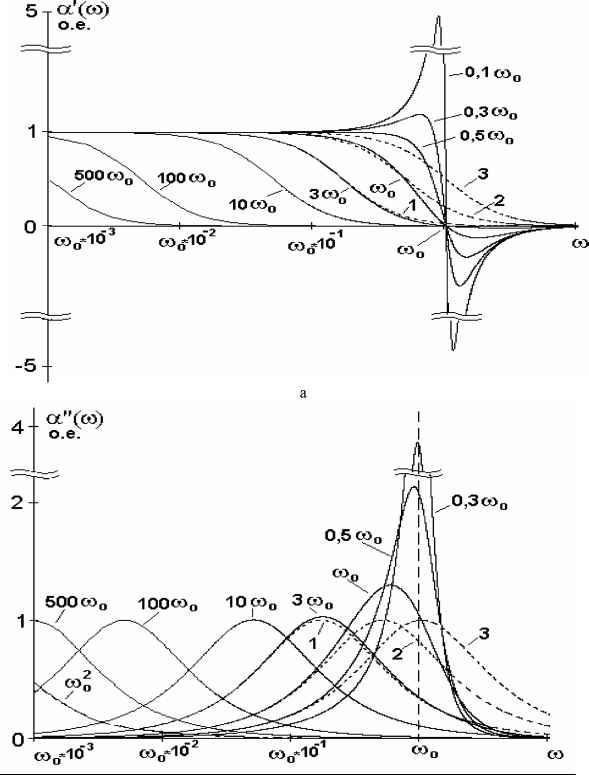

б

Рис. 2

Зависимость действительной (а) и мнимой частей (б) поляризуемости от частоты (функции (13) и (14)) для различных значений коэффициента затухания. Случай в = 00 соответствует сверхбольшим затуханиям (функция (28)), в = 5000 0 - переходная функция. Пунктиром построены графики релаксационной функции (18).

г- + x = qE°- еш. (17)

dt mm2

Это уравнение описывает колебания невесомой частицы в среде с высоким трением.

Комплексная поляризуемость, соответствующая решению уравнения (17), будет:

а(т) =-2--:- =-И--TT - К-ГТ I (18)

mm,2 1 + imr mm2 \ 1 + т2г2 1 + тг )

Присутствие массы в этой формуле обусловлено только принятыми обозначениями, как уже говорилось, в этом случае cc(m) от массы не зависит.

На рис. 2 пунктиром построены графики действительной и мнимой частей релаксационной функции (18). Как видно из рисунка, приблизительно при > 3m0 графики

неупрощенных (13), (14) и релаксационных функций (18) практически полностью совпадают, при меньших затуханиях расходятся. Это означает, что условие (9), которое мы считали границей между резонансным и релаксационным режимом вынужденных колебаний таковым не является и не определяет область применения формулы (18). Для определения этой области составим отношение релаксационной функции (18) к резонансной функции

(12):

?+Г 1 (19)

Возьмём отношение модулей на частоте m0, и определим значения г, при которых это отношение отличается от 1 не более чем на 0,01

VTv =,/7 < 1,01 (20)

-m2/m02)2 +m2r2 m0r

аналогичное выражение даёт квантовая теория. Область применения формулы (16) J/< 0,01m0.

2. Большое затухание, >> m0, выполняется условие (8), колебания релаксационные.

Для гармонического осциллятора это условие означает, что сила инерции становится пренебрежимой по сравнению с силой трения. Поэтому в уравнении (10) отбрасываем первое слагаемое, учитывающее инерционность осциллятора, и получаем уравнение первого порядка [9]:

Это условие выполняется при

т> - (21)

или, если раскрыть обозначение (11), то:

в> 3,50 0. (22)

Таким образом, неравенства (21), (22) определяют область применения полученной нами релаксационной формулы (18), а также релаксационный режим вынужденных колебаний. Заметим, что при выполнении условия (22) функция релаксации (5) переходит в функцию (1), т.к. второе слагаемое в (5) становится пренебрежимо малым. Если взять различие между (18) и (12) в 15% (точность эксперимента), то условие (22) будет выглядеть следующим образом: в > 0,880 0 (т > 1,76/ 00 ), что близко к условию (8), которое в первом приближении

можно считать границей резонансного и релаксационного режимов. Также, грубым признаком релаксационного режима можно считать исчезновение резонансного пика на зависимости a (0) (рис. 2а).

Легко заметить, что уравнение (17) подобно тому, из которого Дебай вывел свои известные формулы [13]. Покажем, что формулы Дебая являются аналогами полученного нами соотношения (18). Используя формулу Борна [2]:

s(0 ) = sm+- (23)

и выражение (18) переходим к комплексной диэлектрической проницаемости:

s(0 ) = е„+ 4 . (24)

s0 m 0 0 1 + i 0 т

где n - концентрация заряженных частиц, участвующих в процессе поляризации, е0-диэлектрическая постоянная, £ж - диэлектрическая проницаемость на высоких частотах. Далее разделяем на действительную и мнимую части:

* (0) = 1 + 1л 12 2 (25),

s0m0 0 1 + 0 т

е\0 ) = ~--(26).

s0m00 1 + 0 т