
|
| |||
|
Разделы
Главная
Сапромат
Моделирование
Взаимодействие
Методы
Инновации
Индукция
Исследования
Факторизация
Частоты
Популярное
Как составляется проект слаботочных сетей?
Как защитить объект?
Слаботочные системы в проекте «Умный дом»
Какой дом надежнее: каркасный или брусовой?
Как правильно создавать слаботочные системы?
Что такое энергоэффективные дома?
|
Главная » Распространение 1 2 Распространение ТМ и ТЕ электромагнитного поля в сужающемся зонде ближнеполевой оптической микроскопии с радиусом отверстия 50 нанометров Арсланов Н.М. (narslan@mail.ru)(1), Моисеев С.А.(1,2) (1)Казанский физико-технический институт КНЦ РАН, Сибирский Тракт 10/7, Казань, 420029, Россия (2)The Graduate School of Information and Communications, Inha University, Incheon 402-751 S. Korea Основываясь на методе поперечных сечений Каценеленбаума в работе развивается подход к расчету светового поля в зонде ближнеполевой микроскопии. Данный подход применен для изучения динамики распространения световых мод в зонде с учетом его сужения, и когда размер выходного отверстия оказывается значительно меньше длины волны света X в вакууме. Получены аналитические выражения для волнового числа мод сужающегося зонда, использование которых существенно облегчает анализ динамики светового поля. Определено влияние угла наклона стенки зонда на поведения амплитуд мод поля при возбуждении зонда монохроматическим источником света. Показано, что форма зонда может приводить к существенному изменению структуры светового поля в выходном отверстии зонда. Найдены соотношения между продольной и поперечными компонентами поля при изменении длины волны. Обнаружены спектральные области нормального и аномального поведения интенсивности поля при изменении длины волны. На основе развитого подхода проведено исследование распространения фемтосекундного импульса света длительность 50 фсек в сужающемся зонде. Ключевые слова: сканирующая ближнеполевая оптическая микроскопия, оптика ближнего поля, зонд, продольная и поперечная поляризация света, нерегулярные волноводы и волокна. PACS numbers: 07.79.Fc; 87.64.Xx; 42.25.Bs, 42.25.Gy 1. Введение В изучении физических свойств поверхности вещества большое внимание привлекает техника сканирующей ближнеполевой оптической (СБО-) микроскопии [1-3]. В настоящее время методы СБО - микроскопии активно применяются в решении прикладных задач физики поверхности [4,5], микроскопии, литографии, записи и хранении информации [6-8], изучении полимеров [9], биологических систем [10-11], а также в изучении фундаментальных вопросов взаимодействия света с атомами и молекулами на поверхности различных веществ, квантовыми точками в полупроводниках [2, 12-15]. Существует ряд модификаций техники ближнеполевой микроскопии [16,17]. В одном из наиболее распространенных ее вариантов свет длиной волны X через оптоволокно попадает в зонд, представляющий собой конусообразное волокно, покрытое металлом. На конце зонда находится отверстие с диаметром значительно меньшим X, что позволяет фокусировать свет на поверхность вещества с площадью S << X2. Диаметр такого выходного отверстия меньше, чем радиус отсечки большинства мод [3], возбуждаемых на входе в зонд, поэтому только малая часть входной энергии поля достигает образца. Как следствие, низкая пропускная способность зонда становится главным фактором, который как ограничивает дальнейшее увеличение разрешения СБО - микроскопа, так и влияет существенно на спектральные, поляризационные характеристики выходного излучения. Полученные первые экспериментальные результаты [18] измерения выходного поля в дальней зоне показывают, что свойства светового поля претерпевают сильное изменение пространственных свойств и поведение поляризации. Для правильной интерпретации информации получаемой из экспериментов по СБО-микроскопии необходимо хорошо понимать детали взаимодействия локализованного светового поля и образца. Для этого, прежде всего, следует знать пространственную структуру и поляризацию светового поля на выходе из зонда, в ближней зоне. Изучение закономерностей распространения излучения в сужающемся зонде и влияния формы зонда на параметры выходного излучения является особенно актуальным для развития этой техники. Исследование этих вопросов является темой настоящей работы. При последовательном теоретическом описании СБО -экспериментов ближнее и дальнее поле следует рассматривать в рамках единого подхода на основе решения уравнения Гельмгольца при граничных условиях, которые сильно усложняются геометрией СБО - микроскопии. Данные решения могут быть получены только с привлечением численных методов, требующих большого расчетного времени [19]. В первой части настоящей работы мы анализируем существующие подходы к проблеме. В теоретической части работы мы развиваем метод расчета пространственной структуры поля в зонде, основанный на теории поперечных сечений Каценеленбаума для нерегулярных волноводов [20], на основе которой в следующей части проводятся численные расчеты поведения светового поля для различных моделей зонда. В заключении обсуждаются основные результаты и вывода, позвляющие использовать полученные результаты для улучшения существующих возможностей ближнеполевой микроскопии. 2. Теоретические подходы к расчету световых полей в СБО-микроскопии Первые теоретические работы [21-25], которые можно использовать для СБО-микроскопии, позволяли рассчитывать коэффициенты прохождения или дифракции поля через отверстие в тонком экране. Позднее, используя эти представления, было учтено влияние конечной толщины экрана из идеального металла с отверстием [26,27], но без учета сужения диаметра отверстия, которое оказывает принципиальное влиние на оптические процессы в зонде СБО-микроскопа. В последующих работах влияние данный вопрос стал предметом ряда исследований. В одной из первых работ [28] изучались особенности возбуждения различных мод в идеальном металлическом зонде под действием внешнего поля, попадающего в зонд через малое отверстие. В дальнейшем значительное внимание было уделено разработке численных методов. Авторами работ [29,30] был предложен разностный метод решения уравнений Максвелла в пространственно двумерной постановке к СБО-микроскопии, однако он не получил применения в силу вычислительных трудностей. В статьях [31-33] развивается общий подход к изучению электромагнитного поля в выходном отверстии зонда и его окрестности, основанный на использовании функции Грина. Однако распространение излучения в самом зонде в рамках данного метода не изучалось. В работах [34-36] разрабатывается 2-х и 3-х мерные модели СБО-микроскопа, основанные на разложении поля в зонде в виде суперпозиции полей от конечного числа мультиполей, при этом основное внимание уделялось лишь изучению диаграммы направленности излучения из простейших двумерных моделей зонда. Зонд можно представить как сужающийся волновод, поэтому для расчета пространственной структуры продольно и поперечно поляризованного электромагнитного поля в зонде можно использовать работы, посвященные нерегулярным волноводам, в которых представлены различные варианты метода поперечных сечений. Теория нерегулярных волноводов активно развивалась в 50-60-х годах в работах [20,37-43] и других. В частности в работах [39-43] поле в зонде разлагается по мембранным функциям в регулярном волноводе данного сечения. Для коэффициентов этих разложений устанавливалась система обыкновенных дифференциальных уравнений второго порядка, которые затем исследовались по методу ВКБ. Похожий вариант этого метода недавно стал развиваться в работах [44-48]. Для одного вида сужения стенки зонда, когда связями между модами можно пренебречь, используя метод ВКБ, авторами найдено приближенное аналитическое решение системы дифференциальных уравнений второго порядка для амплитуд разложения поля по сумме прямой и встречной волнам [48]. В данной работе анализируется поведение амплитуд разложения поля в зависимости от продольной координаты зонда. Однако, для произвольного сужения стенки зонда аналитическое решение не построено и численно не исследовалось. В работах [44-47] поле в зонде раскладывают по модам конуса, учитывая отражение от выходного отверстия. В этих работах не исследовалось влияние физических параметров свойств стенок и геометрии сужения зонда на пространственную структуру поля в зонде, в том числе вблизи выходного отверстия. Отмеченные выше теоретические работы, не дают достаточно полного представления о поведении светового поля в зонде СБО - микроскопии, в том числе комопоненты поля, сильной связанной со стенками зонда (эванесцентного поля). В настоящее время хорошо известно, что эванесцентное световое поле на выходе зонда имеет большую продольную поляризацию [3]. Вместе с тем отсутствует последовательное описание поведения поперечно и продольно поляризованных компонент поля в поперечном сечении реалистических моделей зонда. Неизвестны важные для эксперимента зависимости пространственной структуры продольно и поперечно поляризованного выходного эванесцентного поля от размеров зонда и угла наклона стенок, длины волны излучения и физических параметров неидеальных зондов. В связи с чем остается неясной и вся физическая картина распространения и ослабления излучения в сужающихся зондах с различной геометрией, физическими параметрами стенок, что имеет важное значение в связи со значительным развитием экспериментальной техники. Изучение этих вопросов является основной задачей нашей работы. В результате анализа вышеприведенных работ мы решили следовать методу, предложенному в работах Каценеленбаума [20,49] по изучению электромагнитного поля в нерегулярных волноводах. Данный метод Каценеленбаума (ниже мы введем сокращенное название - К-метод ), на наш взгляд, может описывать физическую картину поведения поля в зонде с учетом реальных физических параметров зонда, влияющих на распространение излучения и удобен для проведения эффективных численных расчетов [50]. Как показывает анализ, важнейшей особенностью поведения поля в сужающемся зонде при расчете К- методом является наличие сильного взаимодействия между соседними модами поля и затухание каждой из мод. Поэтому целью представленной работы явилось изучение эффектов взаимодействия мод и изменение пространственной структуры продольно и поперечно поляризованного светового поля вблизи выходного отверстия при различных физических параметрах зонда. В данной постановке изучаемая нами задача о поле в зонде реализуется в большинстве основных схемах СБО - микроскопии. 3. Основные уравнения метода поперечных сечений (К-метода) Зонд ближнеполевой оптической микроскопии в К-методе рассматривается как закрытый нерегулярный волновод, с поперечным сечением, которое изменяется от большого диаметра на входе до очень малого диаметра на выходе зонда. При изложении К-метода ниже мы главным образом придерживаемся работы [20]. Основная идея К-метода состоит в том, что в любом сечении нерегулярного волновода поле представляется в виде суперпозиции волн обоих направлений, существующих во вспомогательном прямолинейном, регулярном волноводе того же сечения и с тем же распределением s и и, по сечению. Задача об определении поля в сужающемся зонде ближнеполевой микроскопии сводится к задаче нахождения собственных мод поля в регулярном закрытом волноводе и к решению системы обыкновенных дифференциальных уравнений для амплитуд волн, входящих в суперпозицию общего решения. Волноводом сравнения в этой задаче является регулярный волновод, в котором s и ц. во всех сечениях представляют те же функции от x и у, что и в данном сечении нерегулярного волновода, то есть волноводы сравнения для разных сечений z различны. Координатную систему в волноводе сравнения обозначим через x, у, Z Поля собственных волн в волноводе сравнения зависят экспоненциально от Z согласно eihZ, как и в реальном зонде принимается зависимость от z в виде eihz, где от z также зависит вид функций s(x,y,z) и u(x,y,z). Зависимость от частоты примем в виде exp(-icot), тогда уравнения Максвелла приобретут rotE = ik/лЙ, rotH = -iksE. (1) Разложения поля по прямым и обратным модам вспомогательного волновода [20] представляются в виде: E(z) = ХPj (z)EJ (z), H(z) = XPj (z)HJ (z), (2) - СО -СО где поля Е, Н удовлетворяют на стенках нерегулярного волновода тем же граничным условиям, что и поля EJ и HJ на стенках волноводов сравнения; в свою очередь, моды поля ортогональны в каждом поперечном сечении закрытого волновода [51] : jdS ([#mEj] + [HJEm]) = 2khmSjm , (3) S L где hm -волновое число m-ой моды в волокне, подлежащее определению для каждого волновода. Собственные моды волновода сравнения EJ(x,y,z) и HJ(x,y,z) для данного z, удовлетворяют уравнениям Максвелла в регулярном волноводе сравнения, где z выступает фиксированным параметром. Используя уравнения для мод поля в волноводе сравнения, уравнения Максвелла для поля в нерегулярном волноводе сводятся к следующей системе уравнений для коэффициентов разложения Pj , входящие в поле (2) : где по повторяющимся индексам проводится суммирование. После умножения на Hxm,-Hym, -Exm, Ej 1 и интегрирования по поперечному сечению зонда с учетом условия ортогональности (3), система уравнений (4) приобретает вид: d v=°° -P} (z) - ihj (z)Pj (z) = X Sjm (z)Pm (z), (5) dz v=-°o где Sjm - коэффициенты связи мод на стенках нерегулярного волновода сравнения: Sm = --- f dS (Ei-Hm - El-Hm + Em-Hl - Em-Hi ) (6) Jm 2 khj S dz y y dz x x dz y y dz x Значения коэффициентов Pj(z) в начале и в конце нерегулярной части волновода равны амплитудам соответствующих волн в регулярной части. Дальнейшее развитие теории связано с нахождением величин Sjm и hj, и анализом системы уравнений (5). 4. Основные соотношения для волновода переменного сечения с неидеальными стенками Непосредственное применение метода поперечных сечений к волноводам переменного сечения связано с трудностью, которая состоит в том, что в рядах типа (2) поля E, H и поля Em,Hm удовлетворяют различным граничным условиям. Чтобы не оперировать с рядами, неравномерно сходящимися вблизи границы и учесть влияние граничных условий на распространение светового поля в работе [20] волноводу переменного сечения сопоставляется вспомогательный волновод большего постоянного сечения, заполненный материалом с постоянными s и д. При этом свободной от этого материала области соответствует внутренняя область волновода переменного сечения. Для выбранного большего волновода с нерегулярным заполнением применение К-метода дает результаты, которые справедливы для любых значений s и д материала. В предельном переходе jsj-oo вспомогательный волновод становится тождественным исходному волноводу переменного сечения с идеально проводящей стенкой. При этом влияние граничных условий сводится к нахождению коэффициентов связи мод, входящих в общее уравнения данной теории. Для сужающихся волноводов с постоянным диэлектрическим заполнением выражение (6) для коэффициентов связи можно преобразовать в более простое, где интеграл берется уже только по границе перехода сердцевина-стенка [20]. Для учета реальных физических параметры стенки зонда используем граничные условия Леонтовича [52], которые в цилиндрической системе координат принимают вид: E9=ZHz, Ez=-<!H<p (7) где Е, = волновое сопротивление стенок, ц, s магнитная и электрическая проницаемость стенок соответственно, получим для (6): Sjm = 2h h - h ) f dpv(p)r{l-(HH -+SoEJEmЬ (8) где учитывалось, что зонды ближнеполевой микроскопии можно считать немагнитными /0=/i=1, r, ф, z цилиндрические координаты, v(cp) тангенс угла наклона стенки зонда к продольной оси. При вычислении коэффициентов связи можно воспользоваться тем [49, 53], что для электрических мод ее магнитная часть имеет второй порядок малости при разложении в ряд по волновому сопротивлению стенок которое значительно меньше единицы, так как диэлектрическая проницаемость металлического покрытия s 1. Для магнитных мод уже электрическая компонента поля является второго порядка малости по Таким образом, для получения коэффициента связи в первом порядке по Е, можно использовать моды идеального волновода [54,55], а волновое число мод находить в первом порядке по Поля в цилиндрическом волноводе с идеальными стенками с однородным диэлектрическим заполнением ео можно выразить через потенциалы Герца [54]. Для поперечно-магнитных ТМ мод и электрических ТЕ мод поля выражаются через потенциалы Пе и Пт в виде: H =-ik0s0rotne, Eш = rotrotne, (9) HTE = rotrotnm , ETE = ik0rotnm, (10) где ко волновое число света в свободном пространстве. Сами потенциалы удовлетворят уравнению а± nn+а П = 0 и условию нормировки: al J dS ПГ ПГ = 1, al J dS nnTEnnTE = s0, (12) где aП = к2s0 - h2 собственное значение соответствующей моды. Для идеального волновода a = /nj / a , a =vnj / a , а - радиус волновода, vnj, /ц -j-ые нули функции Бесселя n-го порядка и ее производной. После интегрирования (8), учитывая (9)-(11) для симметричного сужения волновода, коэффициенты связи прямых и обратных мод идеального волновода примут вид: S =[l-A ~hCf(-SJm +*J,-mЬ (13) \ s J hj (hj - hm )a TE TTE =i S0 anjMnm + (hjhm - k0s0)n V ( ) (14) I ) - .- I . - ~\Pi.m -°i-m) V147 Sjm ~ \ 1 I / 2 2 I 2 T~ j>m j,-m) SfmTM = t( 1 -A1 krf0 iSjm +Sj,-mЬ (15) k0>4s0 n где jm, так что hjhm. При j=m коэффициент связи будет: 1 dh St,- =---L. (16) j 2hj dz Таким образом, мы упростили коэффициенты связи мод поля волновода, выразив их через волновые числа мод регулярного волновода. Эти волновые числа являются решением трансцендентного уравнения, полученного из граничных условий для мод поля на металлических стенках регулярного волновода [56]: s0 p Jn (aa) i caKn (pa) Kn (pa) Jn (aa) аКП (pa) 1 = hn~s? Jn (aa) Kn (pa) (17) 2 2 2 a pa где штрих - это производная по аргументу функции, а - радиус волновода, 8о, s диэлектрическая проницаемость сердцевины и покрытия, -p2=ko2s - h2, J(x), K(x) - обычная и модифицированная функции Бесселя. Аналитическое решение уравнения (17) получить затруднительно, для чего в работах [36,55] использовались численные методы. Однако, для решения системы уравнений (5) и анализа поведения мод поля при изменении основных параметров зонда, таких как радиус сечения, проницаемость стенок зонда и оптоволокна, а также длины волны излучения, желательно иметь аналитическое выражение для волновых чисел с достаточной степенью точности разложения по волновому сопротивлению. Ниже мы найдем подобное решение для волнового числа мод HE и EH типов в виде разложения в ряд по волновому сопротивлению стенок, следуя методу, предложенному в работе [49]. При этом полученные аналитические решения с высокой точностью согласуются с ранее полученными численными результатами работ [36,55]. 5. Волновое число в волноводе с неидеальными стенками Для определения волновых чисел мод hn в волноводе с неидеальными стенками воспользуемся граничным условием Леонтовича (7), при этом собственные значения разложим в ряд по степеням £<<1: a= ao2+Zai2+ h2= ko2so-a2=ho2-Zai2+. (18) Запишем, участвующие в граничном условии (7) компоненты полей через потенциалы и получим условия, связывающие значения этих функций на контуре сечения: ih--ikoMo-=a2 п т, (19) rocp dr1 a2 Пe = - ik0s0--+ ih r дер (20) Для определения волнового числа магнитных волн вводят вспомогательную функцию Фе=11Пе. Тогда будем иметь систему уравнений:
a2 п т, дФе ., 2 дП гдр АП т +a2 П m Функции Ф и П разложим в ряды: Ф=Ф0е +аФ]е+..., Пт=Пот+аП1т+..., (21) (22) (23) (24) (25) (26) и решая систему уравнений (21)-(24), ограничиваясь первым порядком по 4, используя находим следующее выражение для cti2: формулу Грина НdS(VAU - UAV) = Ids\ V - - U- S C \ dn dn k 0M0 I rdp- П0m2 + A021 rdg>- П0 д2 п 0 с с r dq> Аналогичная схема вычислений имеет место которые находим: (27) и для электрических волн, проделывая a,2 = -ik 0s01 rdcp с К В итоге получим: 1) ТЕ моды: h2- + 4- 2) ТМ моды hid] -щ2) + 42ik0s0 /a, 40 a2 (28) (29) (30) где ho-волновое число соответствующей моды в идеальном волноводе. Представленные на рис.1 и рис. 2 графики описываются найденными решениями (29), (30). Как показало сравнение, данные решения с большой точностью совпадают с численными результатами работы [36]. Отметим, что отличия аналитических решений (29), (30) от численных решений, приведенных на рис.1, 2. не проявляются в масштабе рисунков и становятся заметными лишь за пределами области существования мод. Отметим, что световые моды существуют в зонде, если их волновое число удовлетворяет условиям [36]: 2Re h*Imh<Ime, Re h2-Im h2 >Re s. (31) В частности для моды НЕ11 отличия заметно проявляются при радиусе а< 5 нм, а для моды НЕ21 - при а< 8 нм, Для мод ЕН отличия волновых чисел h, вычисленных по формулам (29), (30) от численно найденных становятся заметны только для мнимых значений h. Вместе с тем аналитические решения для реальной компоненты волнового числа данных мод ЕН совпадают с численным решением на всей области изменении радиуса, что, очевидно, отражает и качественные отличия распространения данных мод в зонде, особенности их взаимодействия со стенками. Вместе с тем, данное сравнение с численными расчетами также указывает на высокую точность выполнимости условий Леонтовича для рассматриваемых задач СБО - микроскопии. Полученные аналитические выражения (29) и (30) для волновых чисел мод поля существенно облегчают анализ светового поля в зонде ближнеполевой микроскопии и значительно снижают время счета для решения системы дифференциальных уравнений, рассматриваемого ниже для ряда конкретных случаев. 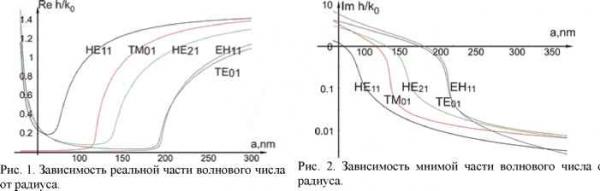 6. Поведение амплитуд ТМом и ТЕом мод поля в сужающемся зонде На основе численных расчетов нами был изучен характер распространения света в сужающемся зонде, для чего также было проведено сравнение распространения светового поляс учетом взаимодействия между модами и без него. В качестве модели зонда мы взяли диэлектрический волновод с s0=2.16, Д0=1 линейно сужающийся от начального радиуса 500 нм до конечного радиуса 50 нм с алюминиевым покрытием s=-34.5+8i и толщиной больше чем скин-слой, составляющий 6 нм. [36]. При решении системы дифференциальных уравнений (5) учитывались моды, удовлетворяющие только условиям распространения в зонде (31) и с волновым числом соответствующих мод идеального зонда h02>0. Другие пространственные моды быстро затухают в зонде из-за наличия большого поглощения, которое определяется слагаемым -ihP в (5). После достижения модой сечения, где условия ее существования (31) не выполняются, она не учитывалась в межмодовых взаимодействиях. Связь между магнитными и электрическими модами (15) для n=0 отсутствует. Исходя из вида граничных условий для амплитуд мод поля TM0m и ТЕ0т на разных концах зонда, были построены алгоритмы нахождения фундаментальной системы решения (5). Искомое решение определялось как линейная комбинация фундаментальной системы решений с коэффициентами, удовлетворяющими условию возбуждения первой моды ТМ01 или ТЕ01 на входе зонда. При численном расчете использовался метод Рунге-Кутта-Фельберга с автоматическим изменением шага для сохранения относительной точности 10 , с которой находилась фундаментальная система решений (5) и определялись величины амплитуд волн. Дальнейшее увеличение точности не приводило к заметному изменению получаемой картины. В силу быстрого изменения граничных условий в зонде, условия существования мод в произвольном сечении зонда и режимы их взаимодействия между собой сильно изменяются, влияя на физическую картину распространения светового поля. Анализ поведения мод поля при данных параметрах излучения позволил установить некоторые общие закономерности распространения мод в этой области пространства (см. рис 3, 4). На Рис. 5 и Рис. 6 приведено решение системы (5) без учета взаимодействия между модами (то есть при условии Sjm=0), которое имеет вид Pj(z)=exp{ihj(~)dz} для зонда с а=450 и длиной 450 нм. Расчеты показали, что взаимодействие между модами приводит к значительной модификации коэффициентов прохождения мод. Сравнение с рис. 3 и рис. 4 показывает, что взаимодействие между модами всегда выравнивает их амплитуды и существенно изменяет картину распространения поля в зонде. Расчеты показали также, что общее прохождение мод начинает быстро уменьшаться после достижения основной модой критического сечения в соответствующем идеальном зонде. При этом суммарная величина энергии поля становится меньше, чем в случае отсутствия взаимодействия между модами. Для сравнения на рис.7 приведено поведение амплитуд различных ТМ мод при распространении в зонде с углом сужения 250. В этом случае длина зонда составляет 965 нм. Приведенные на рисунке графики показывают, что увеличение угла наклона стенки зонда приводит к сильному увеличению коэффициентов прохождения ТМ и ТЕ мод на выходе из зонда. При этом форма зонда будет определять интегральную величину взаимодействия 1 2 | |||||||||||||||
|
| |||