Синтез и анализ алгоритмов автоматической классификации цветных изображений

Ковригин А.В., Хлопов А.Н. (alexhl@list.ru)

Красноярский Государственный Технический Университет

На основе теории распознавания образов синтезирован и исследован алгоритм автоматической классификации цветных изображений, независимый от помех типа освещенность . Приводятся вычислительные эксперименты и анализируются применение полученных результатов в задаче построения машинного зрения.

1. Введение

Актуальной задачей в области искусственного интеллекта является реализация машинного зрения. Комплексное решение данной задачи затруднено, в связи ограниченности вычислительных ресурсов и отсутствия единой теоретической базы. Предпринимались попытки решить задачу на конкретном классе объектов, накладывая на входную информацию дополнительные ограничения. Так некоторые системы идентификации личности основывались на заранее известном положении лица человека на изображении, что значительно сужало область их применения. Требовались значительные ресурсы на синтез и реализацию методов идентификации объектов для разных прикладных задач, из-за невозможности применения ранее внедренных методов распознавания.

Задача состоит в создании алгоритмов анализа изображений способных локализовать и распознавать любые объекты без дополнительной перенастройки или обучения. В данной статье предлагается метод автоматического обнаружения объектов независимо от их размера и расположения на изображении, что является первым этапом при синтезе алгоритмов машинного зрения.

2. Постановка задачи исследования

Пусть задана исходная выборка V = (x, i = 1,n), представляющая собой цветное изображение, где x1 - многомерная случайная величина. Каждая компонента вектора X = (xl, x2, x3) характеризует яркость красного, зеленого, синего цветов соответственно.

Требуется выделить классы на цветном изображении, при заранее не известном их количестве. Под классом подразумеваются фрагмент изображения, пиксели которого близки по цвету.

3. Синтез алгоритма автоматической классификации цветных изображений

Идея предлагаемого похода основывается на построении окрестности R вокруг выбранного класса Q и проверки гипотезы (1) о принадлежности точек из окрестности R классу Q . Задача классификации решается с помощью проверки близости цветовых характеристик X = (X, x2, x3) класса Q с точками x1 = (x{, x2, xJ3 ) R окрестности (2) и дополнительных знаний об объектах на изображении (3). Окрестность R определяется как набор x1 точек, граничащих с классом Q .

Предлагаемая методика:

1. Выбрать i -ую точку из выборки V и отнести её к классу Qm ( включить точку x в

выборку Vm m -го класса, с последующим её удалением из V ).

2. Определить R окрестность класса Qm.

3. Проверить все точки x1 из R окрестности на принадлежность их классу Q m, путем

применения решающего правила (1)

D xix2 , D x

-- <а2 е а <--

x- xJ\\ <Z е а1 <-.- <а2 е а1 <-.- <а2, x] gQm

m(x) -s 11 D1x1x2 D1x1x3 , (1)

eiaa, x1 <£ Qm

где x - точка, принадлежащая классу Qm ,

x1 - точка, принадлежащая R окрестности, Мера близости между точками x и x1 определена как

\\x - x1

(x; - xk) <z (2)

Di x1x2 , Di x1x3 - разностные характеристики, постоянные для отдельных классов на изображении и малозависимые от помех типа освещенность . Dx1x2 - x1 - x2 , Dx1x3 - x1 - x13 , (3)

Z - коэффициент размытости изображения, а1 0.8, а2 1.2 - заранее выбранные пороговые значения.

При условии принадлежности точки x1 из R окрестности классу Q m включить x1 в выборку V m m -го класса, с последующим удалением x1 из V ).

4. При отсутствии точек из R окрестности, которые можно отнести к классу Qm , следует увеличить счетчик классов на единицу m - m +1

5. При отсутствии точек из выборки V , которые можно отнести к классу Qm при заданном коэффициент размытости изображении Z , следует прекратить выполнение алгоритма, в противном же случае перейти к этапу 1.

Эмпирически установлено, эффективность алгоритма автоматической классификации зависит от выбора коэффициента размытости изображения Z . Положение усугубляется отсутствием возможности выбора фиксированного значения Z , минимизирующего ошибку, по причине большого варьирования оптимального Z для разных исходных выборок.

4. Итерационный метод настройки четкости изображения в алгоритме автоматической классификации цветных изображений

Большие значения коэффициента размытости изображения Z делают алгоритм автоматической классификации цветных изображений не чувствительным к цвету точек выборки V. Результатом применения метода с таким значением Z станет существования одного класса, включающего в себя все точки.

Для минимизации ошибок, на первом этапе целесообразно значение параметра Z выбирать достаточно малым Z g [5,8], с целью поставить в соответствие одному

объекту на изображении хотя бы один класс. Для правильного распознавания оставшихся

точек, следует поэтапно увеличивать значение Z на малую величину dZ с целью их равномерного распределения между выделенными классами. Предлагаемая методика:

1. 2.

3. 4.

применить алгоритм автоматической классификации

окрестность и проверить этой окрестности классу

гипотезу о

Q т , путем

Задать значение Z и цветных изображений. Выбрать Qт класс, построить

принадлежности каждой точки x из применения решающего правила (1)

При отсутствии точек из R окрестности, которые могут принадлежать

указанному классу, выбрать следующий класс и перейти к этапу 2.

При отсутствии точек из выборки V, которые могут быть распределены между

указанными классами при заданном уровне Z , увеличить коэффициент

размытости изображения Z на величину dZ и перейти к шагу 2.

Если значение Z достаточно велико ( Z~ [30,35] ) и все точки выборки

V распределены между классами, следует закончить классификацию.

Достижение более точной классификации, осуществляется с помощью перераспределения граничных точек между смежными классами. Каждая граничная точка будет принадлежать тому классу, среднее значение которого MQ (x) ближе к

усредненному параметру

x =11 xj

3 j=i

т (x) = S

M q ( x)

3 Q

i\ q j=i

При условии перехода точки из одного класса в другой по правилу (4), необходимо пересчитать средние показатели этих классов. Для этого следует применять рекуррентные формулы.

n (n -1) n -1

n (n -1) 1=1

где Qt - класс к которому перешла точка xn, Q j - класс который покинула точка xn.

Результатом применения модифицированного алгоритма автоматической классификации цветного изображения служит набор выборок V1, j = 1, т , характеризующих отдельные объекты на изображении.

5. Исследование показателя эффективности алгоритма автоматической классификации цветных изображений

Для исследования эффективности предложенного метода автоматической классификации цветных изображений, алгоритм был протестирован на наборе данных, состоящем из 20 изображений одинакового размера (500х300), полученных при разных условиях освещенности окружающей среды.

Каждое изображение первоначально подвергалось обработке с помощью эксперта, с целью получения указаний учителя (выполнялось выявления объектов и уточнения их

размеров).

Далее изображение поступало на вход алгоритма при разных уровнях dZ g [1,3,5]. Первоначальное значение коэффициента размытости изображения Z было зафиксировано на уровне 5, а максимальное Z взято равным 40.

Далее результаты, полученные с помощью эксперта а и алгоритма а , сравнивались.

Показатель эффективности определялся как оценка вероятности ошибки автоматической классификации объектов на цветном изображении (5).

Р--£ 1(а'а ), (5)

1(а' а ) -

где а1 - указания учителя, а - результаты, полученные с помощью работы алгоритма.

[1, а1

0, а1 -

Полученные показатели эффективности алгоритма автоматической классификации цветных изображений р , усреднялись в пределах одного коэффициента размытости изображения Z и заданного шага dZ (6).

р1- N £ р, n - 20, j -1,3 (6)

Результаты исследования показателя эффективности алгоритма автоматической классификации цветных изображений приведены на рисунке 1.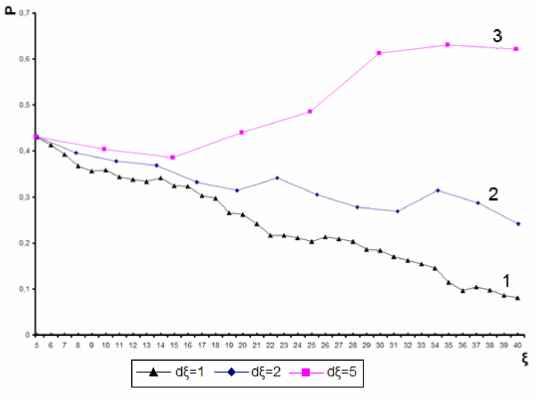

Рис. 1. Зависимость показателя эффективности алгоритма Pj, j = 1,3 от значения коэффициента размытости изображения Z . График №1 показан для значения шага dZ = 1,

второй для dZ = 2 и третий график для dZ = 5 Предлагаемый метод автоматической классификации цветных изображений исследовался на скорость обработки поступающего набора данных. Оценка показателя скорости алгоритма определялась как время, затрачиваемое ЭВМ на проведение автоматической классификации цветного изображения. Оценка скорости алгоритма проводилась для каждого изображения и заданного шага dZ, а полученные значения усреднялись. Результаты исследования показателя скорости алгоритма автоматической классификации цветных изображений приведены на рисунке 2. Тестирование проводилось на ЭВМ с тактовой частотой процессора 2Ghz.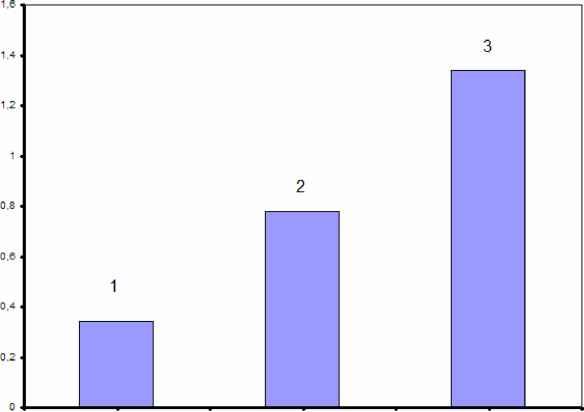

tH=E-

Рис. 2. Зависимость времени выполнения алгоритма автоматической классификации цветных изображений от шага dZ . Столбец № 1 получен для значения шага dZ = 1, столбец №2 для dZ = 2 и столбец №3 для dZ = 5

Исследование алгоритма автоматической классификации цветных изображений показало:

1. Наилучшие результаты, в смысле минимума ошибки классификации, получаются для dZ = 1 . Но скорость алгоритма автоматической классификации при таком шаге достаточно мала.

2. Для достижения приемлемого качества и скорости алгоритма следует комбинировать шаг dZ . Эффективно выбирать значение dZ равное 3, пока коэффициент размытости изображения Z не достигнет уровня 20, т.к. расхождения показателей эффективности алгоритма в интервале Z e [5, 20] несущественны для dZ = 1 и dZ = 3 . Далее предпочтительно dZ выбирать

равным 1, с целью достижения максимального качества автоматической классификации цветных изображений.

Результаты работы алгоритма автоматической классификации цветных изображений представлены на рисунки 3.

(а) (б)

Рис. 3. Результаты применения алгоритма. На картинке (а) показано исходное изображение, на (б) - изображение после применения алгоритма. Локализованные объекты определены как фрагменты изображения, имеющие одинаковый цвет.

6. Заключение

Алгоритм автоматической классификации цветных изображений решает одну из основных задач машинного зрения, выделение объектов из всего многообразия информации, представленной на изображении. Алгоритм не зависит от помех типа освещенность , а также размеров и расположения локализуемых объектов.

Для наиболее быстрой и эффективной работы метода, выявлены рекомендуемые параметры описанного алгоритма. Следует устанавливать первоначальное значение размытости изображения Z равным 5, а шаг выбирать dZ - 3, пока Z не достигнет 20, далее рекомендуется dZ выбирать равным 1 для минимизации ошибки автоматической классификации.

Результаты, полученные с помощью алгоритма автоматической классификации цветных изображений, являются важным этапом в создании таких интеллектуальных систем как: идентификация личности, автоматизации служб безопасности и распознавания рукописного текста.

Литература

1. Лапко А.В., Непараметрические методы классификации и их применение.- Новосибирск: Наука, 1993, 152 с.

2. Sung, K. andPoggio, T. Example-based learning for view based human face detection. In Proceedings from Image Understanding Workshop, Monterey, CA, 1994

3. Rowley, H., Baluja, S. andKanade, T. Neural Network Based Face Detection. Computer Vision and Pattern Recognition. 1996

4. Kanade, T. Picture processing by computer complex and recognition of human faces. Technical report, Kyoto University, Dept. of Information Science. 1973

5. Lucchese L. and Mitra S.K., {{Unsupervised Segmentation of Color Images Based on k-Means Cluster1ng 1n the Chromat1c1ty Plane to appear in Proc. of IEEE Workshop on Content-Based Access of Images and Video Libraries (CBAIVL99), Fort Collins, CO, 22 June 1999.

6. Ziliani F. and Jensen B., {{Unsupervised Image Segmentation Using the Modified Pyramidal Linking Approach Proc. of 1998 Intl Conf. on Image Processing (ICIP98), Chicago, IL, 4-7 Oct. 1998, Vol. III, pp. 303-307.