Многоэлектронные эффекты при аномальном упругом рассеянии фотона атомом бериллия в области К-порога ионизации

Каспржицкий А.С. (anton1982@mail.ru), Хоперский А.Н.,

Явна В.А.

Ростовский Государственный Университет Путей Сообщения, Россия

Дифференциальное сечение упругого рассеяния линейно поляризованного рентгеновского фотона атомом бериллия в области К-порога ионизации рассчитано в нерелятивистском многоконфигурационном представлении волновых функций состояний фотоперехода с учетом эффекта релаксации электронных оболочек в поле вакансии. Результаты расчета носят предсказательный характер.

1. Введение

Исследованию фундаментального процесса упругого рассеяния фотона свободным атомом в области энергий порогов ионизации его глубоких оболочек посвящено большое количество экспериментальных и теоретических работ (см., например, обзор [1]).

Однако в аномально-дисперсионной области рассеяния существующие теоретические модели процесса с использованием приближения независимых частиц при описании волновых функций состояний атома приводят к значительным расхождениям с экспериментом. Результаты недавних исследований [2] показали, что для снятия расхождений теории с экспериментом в аномально-дисперсионной области необходимо выйти за рамки приближения независимых частиц и учесть широкую иерархию многоэлектронных эффектов, сопровождающих процесс поглощения фотона атомом в области энергий порогов ионизации его глубоких оболочек.

В данной работе методы монографии [2], развитые для жесткого рентгеновского диапазона энергий падающего фотона (h® от 600 эВ до 1,5 МэВ), обобщаются на случай мягкого (Йсо от 50 эВ до 1 кэВ) рентгеновского диапазона. Именно, в нерелятивистском многоконфигурационном приближении исследовано влияние монопольной перестройки электронных оболочек в поле вакансии и процессов однократного возбуждения/ионизации на дифференциальное сечение упругого рассеяния линейно поляризованного фотона в области энергий К-порога ионизации атома 4 Be. При этом не рассмотрены Томсоновское рассеяние на ядре, Рэлеевское рассеяние на нуклонах ядра и рассеяние Дельбрюка на виртуальных электрон-позитронных парах, рождаемых кулоновским полем ядра. Их влияние на сечение упругого рассеяния в данном случае несущественно и доминирующим типом процесса является Рэлеевское рассеяние фотона электронами атома [1].

Результаты данной работы могут быть востребованы в контексте, прежде всего, проблем осуществления лазерного термоядерного синтеза и создания рентгеновского лазера, а также решения широкого класса задач физики плазмы, поверхности и других, вплоть до задач астрофизики и космологии.

2. Теория метода

Рассмотрим квантовую систему атом +фотоны с полным гамильтонианом вида:

H = Йа + Hph + W, (1)

где Йа - гамильтониан атома в нерелятивистском приближении, Hph - гамильтониан

свободных фотонов и W - оператор взаимодействия атома с электромагнитным полем в нерелятивистском приближении:

N ( A2 (p { A {)

W = Z -)Vl±± , aх s Afc,0). (2)

1=7 2c c

При теоретическом описании процесса аномального упругого рассеяния фотона атомом дифференциальное сечение имеет вид [2,3]:

§=- (3)

Во втором порядке квантовомеханической теории возмущений по оператору взаимодействия (2) в нерелятивистском приближении для волновых функций состояний атома амплитуда вероятности процесса упругого рассеяния фотона атомом в (3) принимает вид:

Q = (e, e2 )F(0; ш) + А(со). (4)

В (2) оператор векторного потенциала свободного электромагнитного поля в представлении вторичного квантования:

A = 11

2п I-

(kmekr + а+me-kr) (5)

дан как решение [4] в момент времени t = 0 волнового уравнения:

□ A(r, t ) = 0. (6)

Структуры уравнения (6) и линейных по электромагнитному полю слагаемых в операторе взаимодействия (2) обусловлены выбором кулоновской калибровки поля:

drvA(r, t )= 0, (r ) = 0, где <p(r)- скалярная часть 4-потенциала поля Ац = (ф, A), ц = 0,1,2,3 .

В (1)-(5) использована атомная система единиц h = me = e = 1, c - скорость света,

N - число электронов в атоме, p t - оператор импульса и rt - радиус-вектор i - го

электрона, (cikm ) - оператор рождения (уничтожения) фотона с волновым вектором k и

вектором поляризации em, r0 = 2,818 Ю 13 см - классический радиус электрона, e1 и

e2 - единичные векторы поляризации падающего и рассеянного фотона, Q- телесный

угол (угол вылета рассеянного фотона); 9- угол рассеяния (угол между векторами k 1 и

k2), со = й|k J - энергия рассеиваемого фотона.

Квадратичные по электромагнитному полю слагаемые оператора (2) описывают так называемое контактное взаимодействие (в представлении диаграмм Голдстоуна-Хаббарда-Фейнмана в вершине взаимодействия сходятся две фотонные линии и линии частица/дырка) фотона с электронами атома и определяют атомный формфактор (структурная функция атома):

F(0; со) = (0 Е exp(((k r;))()), (7)

который в случае атома с заполненными оболочками в основном состоянии (терм 0) равен:

F (0; ш) = % (4l + 2)J Pi (r ) dr,

k = Ikl = Ik, - k J = 2 sinf

1 2 = c I 2

Исследования роли электронных корреляций в основном состоянии атома при теоретическом описании его формфактора, проведенные для легких атомов 2He,3Li,4Be,5B и 6C , привели к выводу о том, что, по крайней мере, для исследованных атомов корреляционные эффекты не более чем на 1 2% изменяют абсолютные значения формфакторов хартри-фоковского приближения [5]. По этой причине в данной работе построение и расчет формфактора атома 4Be проведены в хартри-фоковском приближении.

Линейные по электромагнитному полю слагаемые оператора (2) описывают процессы поглощения и излучения фотона атомом через его виртуальные возбуждения/ионизацию различной кратности и определяют аномально-дисперсионные слагаемые Крамерса - Гейзенберга - Уоллера полной амплитуды вероятности упругого рассеяния:

Л(ш)= S с? с?--+-- ; (9)

CI? =

U1, 2

(° E(eu p j )m);

г

E0m =-®6 + ; ®m = em - e0

В формулах (7)-(9) определены Pnl (r)- радиальная часть волновой функции nl - электрона, k - вектор рассеяния, E0 - энергия 10} - основного состояния атома, Em - энергия системы атомный остаток + виртуальный фотоэлектрон в m -промежуточном состоянии рассеяния, Гп1 - полная ширина распада nl - вакансии по каналам радиационного и оже - автоионизационного типов, f - уровень Ферми (совокупность квантовых чисел валентной оболочки атома) и символ S означает суммирование (интегрирование) по промежуточным состояниям дискретного (сплошного) спектра различной кратности возбуждения/ионизации всех оболочек атома.

В дипольном приближении (k ri << 1) для фурье-компонент оператора

электромагнитного поля (5) матричный элемент оператора радиационного перехода в (9) может быть определен в форме длины:

dT]= (0;% \Z ф;), (10)

или в форме скорости:

D)=± (0;1S01£р!m;1P. (11)

О m г =1

Как показал наш расчет, различие величин сечения поглощения фотона 1s - оболочкой атома 4Be, рассчитанных с амплитудами (10) и (11) в области дискретного спектра составляет не более 4%, тогда как в области непрерывного спектра соответствует 20%. Поэтому учет корреляций приближения случайных фаз с обменом [6] необходим прежде всего в области непрерывного спектра. В данной работе результаты для области непрерывного спектра приведены в виде среднего алгебраического значения форм длины и скорости.

Появление вакансии в глубокой nl - оболочке атома приводит к эффекту радиальной монопольной (без изменения симметрии состояния) перестройке электронных оболочек атомного остатка в хартри-фоковском поле вакансии [7].

В рамках одноконфигурационного приближения Хартри-Фока при описании волновых функций начального и конечного состояний фотопоглощения атома эффект радиальной перестройки может быть учтен модификацией амплитуд (10) и (11) методами теории неортогональных орбиталей [8,9]. Так в случае поглощения фотона 15 - оболочкой атома 4Be выражение для радиальной (R) части амплитуд (10) и (11) с точностью до членов первого порядка малости принимает вид:

= (150 И mp) , (12)

=- (1501Pmp>. (13)

В (12) и (13) волновые функции Ls0 -, mp - электронов получены решением уравнений Хартри-Фока для конфигураций 1522502 (lS 0) и 15:252 mp(1 P1) соответственно, N1 - произведение интегралов перекрывания волновых функций электронов, не участвующих в переходе и обозначено:

(150 И mp) = j P150 (Г )pmp (r УЖ ,

(150 = J P150 (Г)

Теоретическое описание сечения однократного возбуждения/ионизации основного состояния атома, входящего в структуру аномально-дисперсионного слагаемого A( ) амплитуды упругого рассеяния (9), в качестве алгоритма предполагает решение двух основнхх задач - построение волновых функций начального и конечных состояний однократного возбуждения/ионизации и расчет собственно абсолютных величин и формы сечения фотопоглощения.

Дадим описание этого алгоритма, конкретизировав его для радиационных

переходов из состояний 152 n1l12 (n1l1 > f) в состояния с 15 - вакансией 15 1n1l13 (n1l1 > f) и 15 1n1l12n2l2. Именно такие переходы играют основную роль при теоретическом описании процессов однократного возбуждения/ионизации атома 4Be .

Построение волновых функций начальных и конечных состояний. Оно проводится в два этапа.

На первом этапе для каждой конфигурации из набора 52n1l12} и наборов {15 1n1l13}, {15 1n1l12 n2l2}, на которых строится многоконфигурационная волновая функция начального и конечного состояний фотопоглощения соответственно, решением нелинейных интегро-дифференциальных уравнений самосогласованного поля Хартри-Фока находятся радиальные орбитали остовных и возбужденных электронов.

На втором этапе с использованием полученных на первом этапе радиальных орбиталей строятся базисные волновые функции aZ начального и конечных состояний

фотопоглощения, где a обозначает совокупность квантовых чисел конфигурации определенного типа.

Наконец, волновые функции, определяющие состояния радиационного перехода, представляются в виде:

\ELS) = Е aa* oLS), (14)

где коэффициенты конфигурационного смешивания aaE определяются решением векового уравнения.

Сечение фотопоглощения. Квадрат амплитуды вероятности фотоперехода в состояния (14)

Aels =£aae(aLSd0), D = e£r

a ,=1

определяет интенсивность спектра однократного возбуждения/ионизации. Конкретизируем описанный выше алгоритм для нашего случая. Волновая функция основного состояния атома бериллия определена в виде:

S)=a\ 1s 22s2) + p 1s 22 p2 (1S)) . (15)

Представление (15) связано с тем, что участвующие в нём конфигурации сильно электростатически смешиваются. Об этом говорит тот факт, что конфигурация

1s2 2p1 (1S)) вносит лидирующий (~ 40%) вклад в полную корреляционную энергию

основного состояния атома 4 Be.

Волновые функции конечных состояний дискретного спектра определены в виде:

n2 1s:2s22p) + £2 1s!2pъ) ;

2 v i 2 / \ v (16)

Пm 11s12s2mp) + £m \1sl2p1 (1S}np) , m > 22

Волновые функции конечных состояний непрерывного спектра получены в

следующем приближении. Учтем тот факт, что фотоэлектрон в непрерывном спектре

слабо взаимодействует с остовом. Тогда волновая функция конечного состояния непрерывного спектра определена в виде:

P) = ц| 1s12s2 sp) + cj 1s!2 p2 (1S )sp}, (17)

где коэффициенты u, и c получены из требования минимальности полной энергии электронной подсистемы с отщепленным фотоэлектроном, описываемой волновой функцией u 1s12s2 + c 1s:2p2 (1S). При этом волновая функция sp - получена в соответствующем поле базисной конфигурации в представлении (17).

Ч>( P )

3. Результаты расчета

Аномально-дисперсионное слагаемое Л((й) амплитуды упругого рассеяния (9)

фотона атомом 4Be в области энергий К-порога ионизации получено в трех приближениях.

Приближение 1 - одноконфигурационное приближение Хартри-Фока без учета эффекта монопольной перестройки электронных оболочек в поле 1s - вакансии. Волновая функция mp - фотоэлектрона получена решением уравнения Хартри-Фока для

конфигурации 1s02s2mp(1 P1), т.е. в поле 1s - вакансии с неперестроенным атомным остатком. Волновые функции электронов атомного остатка получены решением уравнений Хартри-Фока для конфигурации основного состояния 1s02s2 (1S 0).

Приближение 2 - одноконфигурационное приближение Хартри-Фока с учетом эффекта монопольной перестройки электронных оболочек в поле 1 s - вакансии. Волновая функция mp - фотоэлектрона получена решением уравнения Хартри-Фока для

конфигурации 1s12s2 mp(1 P1). Волновые функции электронов атомного остатка получены

решением уравнений Хартри-Фока для конфигурации 1s12s2 (2 S2), т.е. учтена радиальная

релаксация атомного остатка в поле образующейся 1 s - вакансии.

Приближение 3 - многоконфигурационное приближение Хартри-Фока с учетом эффекта монопольной перестройки электронных оболочек в поле 15 - вакансии (алгоритм - см. формулы (14),(15), (16) и (17) с m е [2;70]).

Эффект монопольной перестройки электронных оболочек и корреляции приближения случайных фаз с обменом играют существенную роль лишь при энергиях поглощаемого фотона в области порогов ионизации nl - оболочек атома. Поскольку порог ионизации 15 - оболочки атома 4Be сильно отделен от порога ионизации 25 - оболочки (со15 -со25 = 0,114 кэВ), амплитуды радиационного перехода D2 jl±1) и соответствующие

аномально-дисперсионные слагаемые амплитуды упругого рассеяния для 2 - оболочки получены в приближении 1.

Результаты расчета спектральных характеристик лидирующих резонансов сечения рассеяния (3) в приближениях 1 и 2 представлены в таблице.

Результаты расчета сечения рассеяния (3) в приближении 3 приведены на рисунке.

Отметим, что расчет в приближении 3, наряду с уточнением спектральных характеристик резонансов рассеяния, полученных в приближении 2, приводит к появлению в области непрерывного спектра резонансов дискретного спектра, которые обусловлены переходами в состояния с волновыми функциями из (16) (см. рисунок):

11) = -0,2 15:2522p / + 0,951512p3}; 12 = -0,36 151252 3p1) + 0,9315:2 p2 (1S )3 p).

Сформулируем основные результаты данной работы.

1. Учет в теоретическом спектре рассеяния эффекта монопольной перестройки электронных оболочек в поле 1 - вакансии приводит:

а) к сильному подавлению амплитуд и сдвигу в коротковолновую область энергий резонансов упругого рассеяния, рассчитанных в приближении 1 (см. таблицу);

б) к перераспределению интенсивности рассеяния, рассчитанной в приближении 1, из коротковолновой в длинноволновую область спектра рассеяния.

2. Учет эффектов конфигурационного смешивания в начальном и промежуточных состояниях упругого рассеяния, наряду с уточнением приближения 2, приводит к возникновению в теоретическом спектре дополнительных резонансов рассеяния за К-порогом ионизации атома 4Be ёще вне процедуры учета процессов двойного возбуждения/ионизации его основного состояния.

400-

200-

121,5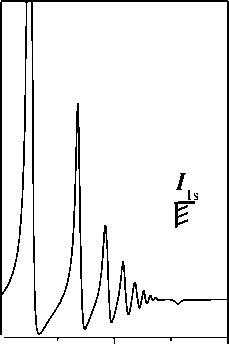

122,0

122,5 124 00, эВ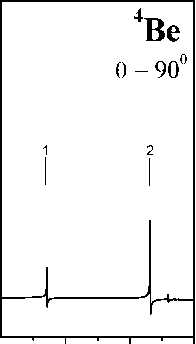

Рис. Дифференциальное сечение (в единицах упругого рассеяния линейно поляризованного

02 /пдадааёт ) аномального (перпендикулярно плоскости рассеяния, 1 , плоскость рассеяния проходит через волновые векторы k 1 и k 2)

рентгеновского фотона атомом 4 Be в области энергий К-порога ионизации. Идентификация резонансов, отмеченных цифрами, дана в тексте. 9 - угол рассеяния, о - энергия рассеиваемого фотона. Указано рассчитанное в приближении 3 положение энергии порога ионизации 1s - оболочки I1s = 122,3 эВ.

Ширина распада 1s - вакансии (расчет данной работы) A1s = 0,016 эВ.

Литература

1. P.P. Kane, L. Kissel, R.H. Pratt, S.C. Roy, Phys.Rep. 140,75(1986)

2. А.Н. Хоперский, В.А. Явна. Рассеяние фотона многоэлектронной системой. М.: Энергоатомиздат, 2004, 276 с.

3. Р.И. Каразия. Введение в теорию рентгеновских и электронных спектров свободных атомов. Вильнюс: Мокслас,1987, 276 с.

4. А.И. Ахиезер, В.Б. Берестецкий. Квантовая электродинамика. М.: Наука,1969,624 с.

5. J.H. Hubbell, I. Overbo, J. Phys. Chem. Ref. Data. 8,69 (1979)

6. М. Я. Амусья. Атомный фотоэффект. М.: Наука,1987, 272 с.

7. V. Schmidt, Rep. Prog. Phys. 55, 1483 (1992)

8. P.O. Lowdin, Phys.Rev.97,1474 (1955)

9. А.П. Юцис, А.Ю. Савукинас. Математические основы теории атома. Вильнюс: Минтис,1973, 480 с.