Моделирование влияния температурной зависимости параметров кристаллической решетки на зонную структуру моноксида бериллия ВеО

Горбунова М.А. (1), Софронов А.А.(1), Кийко В.С.(1), Макурин Ю.Н. (1), Ивановский А.Л. (ivanovskii@ihim.uran.ru ) (2)

(1) Уральский государственный технический университет, г. Екатеринбург (2) Институт химии твёрдого тела УрО РАН, г. Екатеринбург

Среди широкозонных оксидных диэлектриков моноксид бериллия (BeO) выделяется рядом интересных физико-химических свойств [1]. Например, ВеО обладает высокой теплопроводностью, твердостью, керамика на его основе является прозрачным материалом для вакуумного ультрафиолетового, рентгеновского и СВЧ излучений. При модифицировании определёнными примесями BeO-керамика может быть использована в качестве эффективных сцинтилляторов, рабочих тел в термолюминесцентных, экзоэмиссионных и ЭПР-дозиметрах ионизирующих излучений [2-5].

За последний период предпринят ряд теоретических исследований электронной структуры BeO, а также моделирование его некоторых физико-химических свойств. Так, наряду с энергетической зонной структурой, для идеального бездефектного ВеО проведены расчеты распределения плотностей состояний, эффективных масс, зарядовых состояний, параметров межатомных связей, оптических свойств и комптоновских профилей [6-18]. Изучены низкоэнергетические состояния оксида [8], поляризуемость кислорода в решетке BeO [9], диэлектрические свойства [10]. В работе [11] рассчитаны упругие свойства и уравнение состояния BeO. Прогноз изменений электронных и структурных свойств моноксида Ве в условия барической обработки проведен в работах [12-14]. Определена [15] относительная стабильность вюртцитопо-добного BeO - по сравнению с гипотетической графитовой фазой; вычислены энергии дефектов упаковки базисных плоскостей оксида [16]. Модификация электронной структуры оксида бериллия примесями замещения (Li и B) обсуждалась авторами [17].

Недавно авторы [4] обнаружили интересный эффект нелинейного изменения структурных параметров в процессе нагревания <- охлаждения моноксида бериллия.

Целью настоящей работы является теоретическое моделирование электронно-энергетического строения ВеО в зависимости от изменений параметров кристаллической структуры оксида, возникающих при его нагревании <- охлаждении.

Модели и метод расчета. Оксид бериллия кристаллизуется в структуре вюртцита (тип B4, пространственная группа C6mc), составленной плотнейшей упаковкой ионов кислорода с тетраэдрическими и октаэдрическими пустотами.

Рис. 1. Фрагмент кристаллической структуры и зона Бриллюэна

вюртцитоподобного ВеО.

Катионы бериллия образуют гексагональную подрешетку, занимая половину тетраэдрических пустот. Элементарная ячейка содержит по два атома каждого вида. Атомы бериллия расположены в позициях (0;0;0) и (1/3;2/3;1/2), атомы кислорода - в позициях (0;0;z) и (1/3;2/3;1/2+z), Рис. 1. Структура ВеО определяется двумя параметрами (а и с) и внутренним параметром z. Для идеальной структуры вюртцита отношение с/а = 1.633, параметр z = 0.375. Кристалл ВеО немного сжат относительно идеальной В^-структуры вдоль оси с; согласно имеющимся экспериментальным данным, значения структурных параметров ВеО следующие: а = 2.634 - 2.775; с = 4.291 - 4.385 А; с/а = 1.620 -1.627; z = 0.377 - 0.378, см. [1-7].

Для оценки влияния термического изменения параметров кристаллической решетки (Рис. 2) на энергетическую электронную структуру BeO проведена серия расчетов в рамках зонной теории. Элементарная ячейка соответствовала структуре B4 и задавалась параметрами a и с. Относительное смещение плоскостей атомов кислорода и бериллия вдоль оси с принято равным идеальному (0.125 с).

Расчеты проведены первопринципным полно-потенциальным методом ЛМТО (FPLMTO) [19]. Обменно-корреляционный потенциал использован в приближении GGA [20].

В результате получены температурные зависимости полной электронной энергии (Etot, в пересчете на элементарную ячейку; точность расчета при самосогласовании была не хуже 1*10- Ry) и ширины запрещенной щели (AEg). Для крайних точек (T = 80 и 300K) проведен расчет энергетических зон кристаллов вдоль основных направлений зоны Бриллюэна.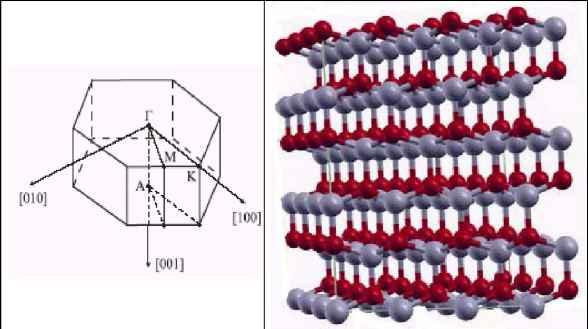

a, A

2.698 т

2.697 +

2.696

и.....*

c, A

4.376 3-

4.375 3-

4.374

~-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1-1

n.....*.....f

heating

.....i

.....I

-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i-i

80 120 160 200 240 280

T, К

Рис. 2. Температурная зависимость параметров решетки BeO согласно [4].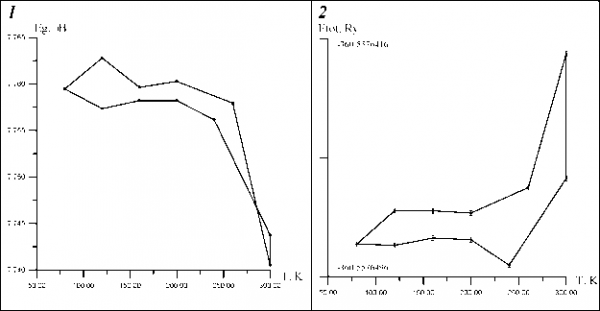

Рис. 3. Температурные зависимости: 1 - ширины запрещенной щели и 2 полной электронной энергии BeO. Расчеты методом FPLMTO.

Результаты. На Рис. 3 приведена температурная зависимость ширины запрещенной щели. Видно, что зависимость AEg(T) зеркально повторяет характерные черты зависимости a,c(T), см. Рис. 2- с пересечением кривых

нагревания и охлаждения в области ~ 280 K. Такая зависимость хорошо коррелирует с изменением объема элементарной ячейки: меньшему Уяч соответствует большее значение AEg, то есть с увеличением взаимодействия между атомами BeO ширина запрещенной щели растет. При нагревании в диапазоне температур 80-260 K изменение AEg керамики BeO составляет 7.759 - 7.763 эВ, а при охлаждении - 7.756 - 7.759 эВ, причем в диапазоне 280300 K значение AEg на кривой нагревания становится меньше величины AEg на кривой охлаждения.

При рассмотрении температурной зависимости полной электронной энергии (Etot, см. Рис. 3) становится очевидным, что кривые нагревания и охлаждения не пересекаются во всем диапазоне температур, а величина Etot меньше на кривой охлаждения при той же температуре. По дисперсионным зависимостям E(k) для крайних точек температурного диапазона (Рис. 4) можно видеть, что порядок следования энергетических зон в BeO не изменяется.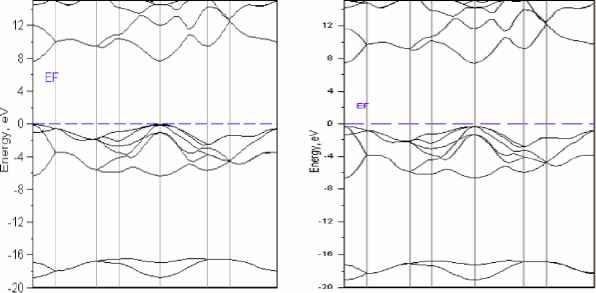

г A L М г К Н А

Рис. 4. Энергетические зоны ВеО для экспериментальных параметров решетки при Т = 80 (слева) и 300K (справа). Расчеты методом FPLMTO.

В целом, результаты расчетов в совокупности с приведенными экспериментальными данными позволяют как вычислить термические коэффициенты линейного расширения (вдоль и поперек оси с (а -продольная и а -поперечная)), так и связать эти величины с механическими характеристиками оксида бериллия (модулем Юнга, упругими коэффициентами). Соответствующие вычисления в настоящее время проводятся.

Литература

[1]. Беляев Р.А. Окись бериллия. - М.: Атомиздат, 1980. [2]. Kiiko V.S. Refract. Industr. Ceram., 2004, 45, 266.

[3]. Кийко В.С., Макурин Ю.Н., Дмитриев И.А., Софронов А.А., Ивановский

А.Л. Стекло и керамика. 2001, 58, 19. [4]. Кийко В.С., Софронов А.А., Макурин Ю.Н., Ивановский А.Л. Стекло и

керамика. 2003, 60, 22. [5]. Кийко В.С., Дмитриев И.А., Макурин Ю.Н., Софронов А.А., Ивановский

А.Л. Физ. химия стекла. 2004, 109. [6]. Xu, Y., Ching W. Phys. Rev., 1993, B48, 4335.

[7]. Lichanot A., Chaillet M., Larrieu C., Dovesi R. Chem. Phys.,1992, 164, 383.

[8]. Irisawa J., Iwata S. Theor. Chim. Acta, 1992, 81, 223.

[9]. Fowler P.W., Munn R.W., Tole P. Chem. Phys. Lett., 1991, 176, 439.

[10]. Darrigan C., Rerat M., Mallia G., Dovesi R. J. Comp. Chem., 2003, 24, 1305.

[11]. Milman V., Warren M.C. J. Phys.: Cond. Matter, 2001, 13, 241.

[12]. Park C.J., Lee S.G., Ko Y.J., Chang K.J. Phys. Rev., 1999, B59, 13501.

[13].Boettger J.C., Wills J.M. Phys. Rev., 1996, B54, 8965.

[14]. Van Camp P.E., Van Doren V.E. J. Phys.: Cond. Matter, 1996, 8, 3385.

[15]. Lichanot A., Baraille I., Larrieu C., Chaillet M. Phys. Rev., 1995, B52, 17480.

[16]. Chisholm J.A., Bristowe P.D. J. Phys.: Cond. Matter, 1999, 11, 5057.

[17]. Софронов А.А., Еняшин А.Н., Кийко В.С., Макурин Ю.Н., Ивановский

А.Л. Электронный журнал Исследовано в России 2003, 142, 1693 /http:

zhurnal.ape.relarn.ru/articles/2003/142.pdf [18] Макурин Ю.Н., Софронов А.А., Кийко В.С., Емельянова Ю.В., Ивановский

А.Л. Ж. структ. химии. 2002, 43, 557. [19] Savrasov S. Phys. Rev., 1996, B54, 16470.

[20]. Perdew J.P., Burke K., Ernzerhof M. Phys. Rev. Letters 1996, 77, 3865.