
|
| |||
|
Разделы
Главная
Сапромат
Моделирование
Взаимодействие
Методы
Инновации
Индукция
Исследования
Факторизация
Частоты
Популярное
Как составляется проект слаботочных сетей?
Как защитить объект?
Слаботочные системы в проекте «Умный дом»
Какой дом надежнее: каркасный или брусовой?
Как правильно создавать слаботочные системы?
Что такое энергоэффективные дома?
|
Главная » Компьютерное моделирование Компьютерное моделирование динамических процессов в спиновом стекле Лесных Ю.И. (lyis@yandex.ru) Тольяттинский государственный университет Спиновыми стеклами называют неупорядоченные магнетики, в которых энергия обменного взаимодействия случайным образом меняет не только величину, но и знак. В таких системах с конкурирующими взаимодействиями, в отличие от обычных магнетиков, с понижением температуры дальнего магнитного порядка не возникает. Но не происходит и медленного постепенного замораживания спинов. Ниже некоторой, достаточно хорошо фиксируемой на эксперименте температуры магнетик переходит в новое состояние, не имеющее аналогов в упорядоченных системах. Характерным свойством этого состояния является чрезвычайно медленная релаксация [1]. Типичные времена установления равновесия, во всяком случае, превосходят 104 - 105с. Одновременно наблюдаются явления необратимости статических свойств. Так как энергия обменного взаимодействия сильно зависит от расположения магнитных и немагнитных атомов, то в классе неупорядоченных магнетиков большинство веществ принадлежит к спиновым стеклам [2]. В настоящее время известно огромное число спиновые стекол - металлов, диэлектриков и полупроводников; разбавленных сплавов (т. е. с малой концентрацией магнитных атомов) и концентрированных; кристаллических и аморфных веществ. Динамические процессы в спиновом стекле очень трудны для представления и наблюдения, поэтому существует потребность в компьютерном моделировании этих процессов. Компьютерное моделирование осуществлялось на языке Turbo Pascal 7.0. Наряду со всеми преимуществами, которые Turbo Pascal 7.0. унаследовал от предыдущих версий Turbo Pascal, в нем были произведены изменения и улучшения. Во-первых: появилась возможность выделять определенным цветом различные элементы исходного текста (зарезервированные слова, идентификаторы, числа и т.д.), позволяющая устранять ошибки на этапе ввода исходного текста. Во-вторых: язык программирования Turbo Pascal 7.0. был расширен, что представило пользователю дополнительные возможности при решении задач. В-третьих: был улучшен компилятор, вследствие чего коды программ стали более эффективными. В-четвертых: был улучшен интерфейс пользователя [3]. Лингвистическая концепция Паскаля пропагандирует системный подход, выражающийся, в частности, в расчленении крупных проблем на меньшие по сложности и размеру задачи, легче поддающиеся решению. Основные принципы Паскаля таковы: Структурное программирование. Суть его заключается в оформлении последовательностей команд как замкнутых функций или процедур и в объединении данных, связанных по смыслу, в сложные структуры данных. Благодаря этому повышается наглядность текста и упрощается его отладка. Проектирование сверху вниз. Программист разбивает свою задачу на несколько более простых, после чего каждая из задач решается по отдельности. Затем компонуются результаты проектирования простых задач, и решается задача проектирования сверху вниз в целом. Язык Паскаль выбирался исходя из различных причин. Паскаль довольно простой в обращении, имеет красивую, стройную структуру программы, а так же в отличие от других простых языков (например, Бейсика) имеет широкие возможности графического редактора в совокупности с текстовым. Язык Паскаль разработан с учетом принципов структурного программирования, которое на современном этапе признано действенным методом рационализации труда программиста. Для структурированных программ характерны легкость отладки и корректировки, низкая частота ошибок. Кроме этого, такие программы легко сопровождать и модифицировать без учета разработчиков. Паскаль обладает полным набором структурных типов данных, таких как простые переменные, массивы, файлы, множества, записи, записи с вариантами, ссылочные переменные. Введение структурных типов данных способствует созданию эффективных алгоритмов. Особо следует отметить надежность Паскаль-программ, которая достигается иногда за счет избыточности, например, обязательного описания переменных и соответствующих типов. Надежность достигается также за счет простоты и естественности конструкций языка, соответствующих логическому мышлению разработчика программ. Это свойство языка помогает в нахождении логических ошибок в программе. Язык содержит ряд удачных изобразительных средств помогающих организовать ветвление в программе без использования операторов перехода, что способствует простому пониманию алгоритма. В литературе отмечается также комфортабельность языка , заключающаяся в том, что язык должен давать не только определение алгоритма, но это определение должно быть достаточно понятным. В Турбо Паскале разработаны программные средства для построения графических изображений на экране персонального компьютера. Набор операторов стандартного Паскаля относительно мал и легко изучаем. В программе используются модули Crt и Graph. Модуль Crt содержит ряд подпрограмм, предоставляющих возможность программам, работающим под DOS, эффективно управлять такими характеристиками персонального компьютера, как режимы экрана, расширенные коды клавиатуры, цвета, окна и звуковые сигналы. Модуль Crt может использоваться только в программах, работающих на персональных компьютерах IBM PC или полностью совместимых с ними. Одним из основных преимуществ использования модуля Crt является повышение скорости и гибкости при выполнении операций работы с экраном. При использовании модуля выводимая информация посылается базовой системе ввода-вывода (BIOS) или, для еще большего ускорения операций, непосредственно в видеопамять. Для создания графических изображений в языке Turbo Pascal 7.0. предназначен стандартный библиотечный модуль Graph. Он представляет собой библиотеку программ, которая полностью обеспечивает управление графическими режимами различных адаптеров дисплеев: CGA, EGA, VGA, MCGA, Hercules, PC 3270, AT&T 6300 и IBM 8514. Библиотека содержит около 80 графических процедур и функций, а также десятки стандартных констант и описаний типов данных. Сам модуль представляет собой отдельный файл GRAPH.TPU, который не входит в состав библиотеки TURBO.TPL, и чтобы обеспечить возможность работы с графикой, нужно сделать файл GRAPH.TPU доступным для компилятора. Программа рассчитана для работы с компьютером PC IBM, оснащенным адаптером VGA с объемом видеопамяти 256 килобайт. Программа имеет 3 основные процедуры: Risov для рисования спинов в узлах решетки, ChangePages для смены отображаемой и активной страниц, Povorot для поворота спинов на различные углы. Основной цикл программы Repeat until false, в котором последовательно осуществляется обращение к этим процедурам, содержит условный оператор для выхода из программы. Для построения на экране объемных фигур потребовалось использование следующих теоретических сведении по стереометрии: Проекция является важнейшим понятием в 3D графике [4]. Собственно говоря, на экране дисплея изображаются проекции объемных тел. Проекция получается следующим образом: все точки объёмного тела движением вдоль луча проектирования l переносятся на картинную плоскость, которая отображается на экране. Существует две разновидности проекций: параллельная и перспективная. Разница между ними заключается в том, что для первой лучи проектирования параллельны, в то время как для перспективной они сходятся в точке наблюдателя. Перспективная проекция точнее параллельной, но имеет более сложный математический аппарат и применяется для объектов со значительной протяжённостью в глубину. Если при параллельном проектировании картинная плоскость перпендикулярна линиям проектирования, то такая проекция называется аксонометрией [4]. Имеется три вида аксонометрии: изометрия, диметрия и триметрия. При изометрии проекции координатных осей сходятся под углом в 120°, при этом координатные составляющие точки откладываются на осях в едином масштабе. Для диметрии используется два масштаба: один для осей OY и OZ, другой, в два раза меньший -для оси ОХ. Оси ОХ и OY пересекаются под углом 135°. Для изометрии проекция точки P(x,y,z) на экране определяется по формулам: где а - коэффициент общего увеличения изображения, в - коэффициент, компенсирующий горизонтальное искажение для графических режимов с разрешением Н*У: ХХ0 и УУ0 - координаты точки экрана, в которую проектируется начало пространственной системы координат. Изображение многогранника сводится к изображению всех его видимых граней. Грань рисуется следующим образом: определяются проекций всех её вершин и через эти точки строится закрашенный многоугольник. Цвет закраски зависит от того, является ли изображаемая грань освещённой или затенённой - этот приём делает изображение реалистичнее. Для построения изображения многогранника нужно определить два вектора, выходящих из начала координат: l - вектор, направленный к наблюдателю параллельно линиям XX = а/в( y - x) - + XX, 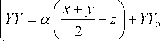 4s )=н x x ,y y z z cos\----- - Простейший способ анимации (мультипликации) заключается в следующем: стирается изображение объекта и рисуется новое, но в другом положении. Этот способ приводит к нежелательным мерцаниям, особенно если это изображение достаточно сложное. Поэтому в данной работе мы используем другой приём, основанный на возможности графических программ работать с несколькими страницами. Для мультипликации достаточно двух - одна страница с нарисованным изображением отображается на экране, на другой, невидимой, подготавливается новый кадр. Затем страницы меняются местами. На компьютерах с проектирования. Для изометрии его составляющие равны lx = ly = lz = 1; s - вектор в направлении к источнику освещения. Построение многогранника осуществляется по следующей схеме: для каждой грани 1) определяется ориентация грани в пространстве вектором нормали n векторное произведение n = а хc . Векторы находятся в плоскости грани и определяются по первым трём её вершинам А, B и С. Составляющие нормального вектора определяются по известным из векторной алгебры формулам: г Пх = ayCz - azCy Пу =-axCz + azCx . n = а c - а c z x у ух 2) определяется, является ли грань видимой (лицевой). Если угол между нормалью и вектором l острый, то грань видимая. Это определяется скалярным произведением nl = nxlx + nyly + nzlz , которое, в случае острого угла, положительно. 3) для лицевой грани определяется, является ли грань освещённой по знаку ns = nxsx + nysy + nzsz и рисуется грань. Интенсивность цвета закраски принимается равной I = I0 +11 cos(n, s), первое слагаемое обусловлено рассеянным освещением, второе учитывается только для освещённых граней и пропорционально косинусу угла между нормалью к поверхности и источником света (закон косинусов Ламберта). Косинус этого угла определяется по соотношению: S nxSx + nySy + nzSz
Ф = У Ф Z = где x, у, z - координаты точки до поворота; х', у', z - координаты той же точки после поворота; Ф - матрица вращения 3*3. Любой поворот можно представить как три последовательных поворота вокруг осей OX, OY и OZ на углы фх, фу и фz соответственно. Матрицы, таких поворотов имеют особенно простой вид: f 1 0 0 0 cos q>x sin q>x 0 - sin p cos p 0 sin q> 0 f cos q>z sin q>z 0 sin cp z cos (p z 0 V 0 0 Программа выводит на экран вращающиеся спины, и позволяет более детально представить динамические процессы в спиновом стекле, моделирование этих процессов, создание модели спинового стекла и его поведение во внешнем магнитном поле, а также прогнозирование состояния спинового стекла в зависимости от изменения температуры. sin p У 0 cos p У Литература 1. Доценко В.С. Критические явления в спиновых системах с беспорядком Успехи физических наук. 2001. Т.164. №5. С. 524. 2. Эфрос А.Л. Физика и геометрия беспорядка. М.: Наука 1982, 176 с. (Серия: Библиотечка Квант ). 3. Турбо Паскаль 7.0. 2-е издание. Киев: Издательское бюро BHV. 1996, 448 с. 4. Мишин Д. Д. Магнитные материалы. М.: Высшая школа. 1991, 384 с. объёмом видеопамяти 256 килобайтов наибольшим возможным разрешением, допускающим многостраничный режим, является 640 х 350. Поворот многогранника можно представить в виде |
|
| |||