Реализация методов манипуляции объектами в интерактивных системах визуализации

А. С. Тотмаков А. С. (totmakov@mail.ru) OOO Luxoft

Рассматриваются методы манипуляции объектами в трехмерном пространстве, используемые при построении интерактивных систем визуализации реального времени

Под манипуляцией, подразумевается выполнение действий или приемов, направленных на изменение позиции, ориентации, формы, анимация объектов, источников освещения и виртуальных камер. Манипуляция объектом осуществляется посредством применения к нему одной или нескольких базовых трансформаций. Под базовыми трансформациями подразумеваются перемещение, вращение, масштабирование, сдвиг, соединение трансформаций, трансформации твердого тела и нормалей и обратная трансформация. представляющих собой перемещение, вращение, масштабирование, сдвиг.

Трансформация является базовым инструментом для манипулирования геометрией. К большинству графических программных интерфейсов (graphic API) относятся функции для обработки матриц, с помощью которых реализуются множество трансформаций.

Матрицы, выполняющие перемещение, вращение, масштабирование, отражение и сдвиг, являются аффинными, т. е. такими, при которых параллельные линии после преобразования остаются параллельными.

Однородные координаты

Точка представляет собой некоторую позицию в пространстве, тогда как вектор -это направление, не имеющее позиции. Используя матрицы размерностью 3х3 (для трехмерного пространства), возможно выполнять такие линейные трансформации, как вращение, масштабирование и сдвиг координат. Однако при этом невозможно выполнить перемещение. Это не относится к векторам, так как перемещение для них не имеет смысла, но для точек имеет важное значение.

Для преобразования как точек, так и векторов вводятся однородные координаты (homogeneous coordinates), в которых матрицы 3х3 дополняются до размера 4х4, а трехмерные точки и векторы обзаводятся еще одним элементом. Таким образом, однородный вектор p будет представлен как p=(pxpypzpw) [1]. Для векторов pw=0, а для точек pw =1. При проецировании могут использоваться различные значения pw. В случае, если pw не равняется нулю или единице, для получения однородных координат необходимо произвести деление всех компонентов на pw. Тогда однородные координаты будут иметь вид (pxpw, pypw, pzpw, 1).

Матрица M3x3 дополняется до однородной матрицы размерностью 4х4 следующим образом:

M4 x 4 =

0 0

m02 m12 m22 0

0 0 1

Вместо матрицы М могут быть матрицы вращения, масштабирования или сдвига, которые будут преобразовывать как точки, так и векторы [2]. Для перемещения используются дополнительные элементы расширенной матрицы. Типичная матрица перемещающая точку на вектор t, будет иметь вид

0 1 0 0

0 0 1 0

В

Легко проверить, что вектор v=(vx,vy,vz,0) не изменяется после преобразования Tv. то же время точка p=(px,py,pz,1) после преобразования Tp будет иметь вид (px+t,py+t,pz+t,1), т.е. будет перемещена на вектор t. Далее будет рассмотрено несколько однородных преобразований.

Перемещение

Матрица перемещения Т позволяет изменить позицию объекта, который перемещается на вектор t = (tx, ty, tz) (рис. 1).

T(t) = T(tx, ty, tz)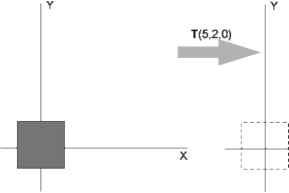

Рис. 1. Преобразование матрицы перемещения T(5,2,0)

Вращение

Несколько более сложный набор трансформаций представляется матрицами вращения Rx(<f>), Ry(#>), Rz(<p), которые используются для вращения объекта на ф радиан относительно оси x, y, z в следующем порядке [3]:

Все матрицы вращения ортогональны, т.е. R = R . Это свойство также сохраняется для комбинации любого числа таких матриц. Обратную матрицу, Ri~1(() = Ri(-() возможно найти вращением в обратную сторону вокруг той же оси. Определитель матрицы вращения всегда равен единице.

Предположим, что нам необходимо повернуть объект на ф радиан вокруг оси z, с центром вращения в точке p (рис. 2).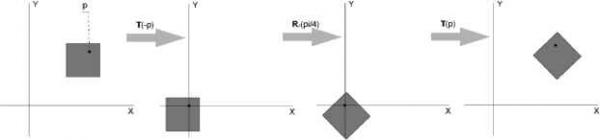

Рис. 2. Вращение объекта вокруг заданной точки

Поскольку вращение вокруг точки характеризуется тем, что сама точка не преобразуется вращением, трансформация начинается с перемещения объекта так, чтобы точка p совпала с началом координат. Это перемещение описывается как T(-p). Далее следует собственно вращение Rz((p). Затем объект перемещается обратно: T(p). Тогда преобразование Х будет иметь вид X = T(p) Rz(q>) T(-p) [4].

Масштабирование

Матрица масштабирования S(s) = S(sx, sy, sz) используется для масштабирования объекта с коэффициентами sx, sy, sz вдоль осей x, y, z соответственно. Это означает, что масштабирование может применяться для уменьшения или увеличения объекта.

Операция масштабирования будет однородная, если sx=sy=sz, и неоднородная в противном случае. Обратная матрица S-1(s) = S(1/sx, 1/sy, 1/sz).

Еще одним при другом методом создания однородной матрицы масштабирования является использование однородных координат [3]. Например, для того, чтобы произвести однородное масштабирование с фактором 5, можно использовать следующие матрицы:

Использование правого нижнего элемента для создания однородной матрицы масштабирования может быть неэффективным, так как в этом случае необходимо производить деление в процессе усреднения (homogenization process). Если правый нижний элемент равен единице, деления не происходит.

Если одно либо три значения фактора s отрицательны, создается матрица отражения (reflection matrix), также называемая зеркальной матрицей (mirror matrix). (В некоторых публикациях матрицей отражения называют матрицу, все компоненты фактора s которой равны -1, s = (-1, -1, -1)). Обычно в случае использования матриц отражения необходима дополнительная обработка. Например, треугольник с перечислением вершин против часовой стрелки (counter-clockwise order) преобразуется в треугольник с перечислением вершин по часовой стрелке (clockwise order). Изменение их порядка перечисления может вызвать неправильное освещение полигона и неправильную работу алгоритма отброса невидимых треугольников (back-face culling). Для того чтобы узнать, является ли данная матрица матрицей отражения, необходимо рассчитать определитель дополнительного минора для правого нижнего элемента, т.е. для левой верхней матрицы размерностью 3х3. Если определитель отрицательный, то это матрица отражения.

Предположим, необходимо масштабировать объект в определенном направлении. С помощью матрицы S производится масштабирование только вдоль осей x, y и z. При масштабировании в другом направлении требуется составная трансформация. Предположим, масштабирование необходимо произвести вдоль ортонормированных право-ориентированных векторов f,f,f. Для начала построим матрицу F:

F = (fx fy fz 0

V 0 0 0 1 /

Координатная система строится из полученных векторов, далее используется стандартная матрица трансформации и затем осуществляется обратное преобразование. При этом требуемое преобразование Х будет иметь вид X = F S(s) FT.

Сдвиг

Другой класс трансформаций - это набор матриц сдвига (shearing). Такие трансформации могут быть использованы для искажения или деформации объекта. Существуют шесть базовых матриц сдвига: Hxy(s), Hxz(s), Hyx(s), Hyz(s), Hzx(s), Hzy(s). Первый индекс указывает на координату, которая будет изменена матрицей сдвига, второй индекс - на координату, по которой будет производиться сдвиг. Матрица сдвига может иметь вид

(10 s 0

0 10 0

0 0 10

v0 0 0 1J

Следует отметить, что индекс может быть использован для нахождения местоположения параметра s в матрице. (Координаты y и z не изменяются, тогда как координата меняется на сумму старого значения и фактора s умноженного на координату z) (рис. 3).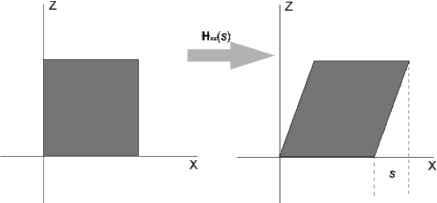

Рис. 3. Сдвиг единичного прямоугольника матрицей Hxz(s).

Обратной матрицей сдвига является матрица сдвига в противоположном направлении: т.е. Hyx-1(s)=Hyx(s). Определитель любой матрицы сдвига равен единице. Следовательно, это есть преобразование, сохраняющее объем.

Совмещение трансформаций

Вследствие того что операция произведения матриц некоммутативна , важен правильный порядок применения трансформаций. Другими словами, совмещенная трансформация зависит от порядка следования составляющих трансформаций.

Предположим, необходимо применить две трансформации - S и R: S(2; 0.5; 1) масштабирует объект по x-компоненте с фактором 2 и по y-компоненте с фактором 0.5, Rz(n/6) вращает на л/6 радиан против часовой стрелки вокруг оси z. Матрицы могут быть перемножены двумя способами с совершенно различным результатом (рис. 4).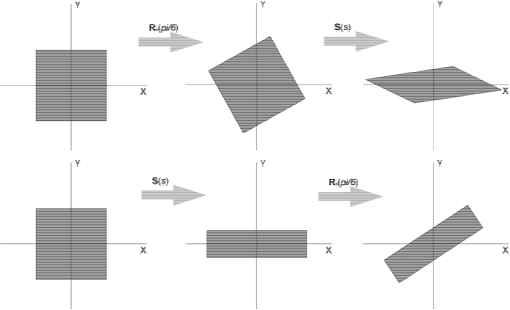

Рис. 4. Зависимость порядка перемножения матриц

Для повышения эффективности процесса целесообразно совмещение последовательности матриц в одну [3]. Предположим, что есть модель, составленная из сотен тысяч вершин, и необходимо произвести масштабирование, вращение и перемещение. Вместо того чтобы последовательно умножать все вершины на три матрицы, можно один раз умножить на совмещенную матрицу, которая будет иметь вид C=TRS. При одном подходе применяется матрица масштабирования S, поэтому она стоит

в правой части выражения. Этот порядок предполагает, что TRSp=T[R(Sp)]. При другом распространенном в компьютерной графике подходе используют матрицы, в которых вектор сдвига располагается в нижней строке. В этом случае порядок умножения матриц должен быть обратным, т. е. порядок применения должен читаться слева направо. Имеется ввиду , что векторы и матрицы записаны в виде строк, поскольку векторы представляют собой строки. В статье использовалась запись в виде столбцов.

Трансформация твердого тела

Трансформация, при которой изменяются только позиция и ориентация объекта, называется трансформацией твердого тела (rigid-body transform). Для нее свойственно сохранение длин и углов [5].

Любая трансформация твердого тела X может быть определена матрицей, состоящей из композиции матрицы перемещения T(t) и матрицы вращения, R. Таким образом, матрица Х имеет вид

X = T(t)R

Обратная матрица

X-1 =(T(t)R)-1 R1 T(t)-1 =RTT(-t).

вычисляется

следующим

образом:

Трансформация нормалей

Одна и та же матрица может быть использована для единообразной трансформации точек, линий, полигонов и других геометрических примитивов. Однако эта же матрица не всегда используется для преобразования важной геометрической сущности - нормали к поверхности (либо нормали, заданной в вершине для ее корректного освещения). Нормали должны преобразовываться матрицей, полученной транспонированием матрицы, обратной к той, которая использовалась для преобразования геометрии, т. е. при условии преобразования матрицей М. Для преобразования нормалей необходима матрица N вида, ЛКМ^рис. 5).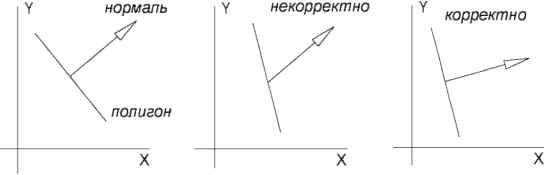

Рис. 5. Примеры некорректной и корректной трансформации нормалей.

Если известно, что матрица ортогональна, (т. е. это матрица вращения), нет необходимости рассчитывать обратную матрицу. Для трансформации нормалей можно применять саму матрицу, так как она будет обратной к ортогональной, являясь транспонированной матрицей. Двойное транспонирование дает нам исходную матрицу. Более того, перемещение не изменяет направление вектора, следовательно, любое количество перемещений может быть выполнено без изменения нормалей.

Следует отметить, что вопрос преобразования нормалей неактуален в системах с автоматическим расчетом нормалей к полигону после трансформации (например, через векторное произведение граней треугольника). Однако очень часто вершины, составляющие треугольник, уже содержат нормали, используемые для освещения, и в этом случае необходимо корректно преобразовывать нормали.

Расчет обратной матрицы

Для нахождения обратной матрицы можно воспользоваться одним из трех способов нахождения обратного преобразования:

Если матрица представляет собой единственную трансформацию либо набор простых трансформаций, обратная матрица находится следующим образом: если M=T(t)R(y), то M-1=R(-()T(-t).

Если известно, что матрица ортогональна, тогда обратная матрица равна транспонированной: M1=MT. Любая последовательность поворотов является ортогональной матрицей.

В общем случае для расчета обратной матрицы следует воспользоваться методом сопряжения, либо правилом Крамера, либо методом исключения Гаусса. Правило Крамера и метод сопряжения наиболее предпочтительны, так как в современных системах следует избегать условных выражений с целью уменьшения ошибок предсказания центрального процессора (тестами корпорации Intel было показано, что на процессоре Pentium III метод исключения Гаусса занимает 1074 процессорных цикла, правило Крамера - s46 циклов, правило Крамера с использованием потоковых инструкций процессора (Intels Streaming SIMD Extensions) - всего 210 циклов [6]).

Программная реализация

Рассмотренные методы манипуляции объектами реализованы программно в составе интерактивной системы визуализации реального времени. Для функционирования системы визуализации необходима операционная система Win9x,NT,XP, поддержка видеокартой версии OpenGL 1.2. Рекомендуемая операционная система WinXP и поддержка видеокартой версии OpenGL 1.5.

Литература

1. Смирнов В. И., Курс высшей математики, том 3. Часть 1. - М.: ФМЛ, 1974.

2. Streaming SIMD Extensions - inverse of 4x4 Matrix. Order Number 245043-001. Intel Corp. March 1999. developer.intel.com/vtune/compilers/cpp/matrix lib.htm.

3. Курош А. Г., Курс высшей алгебры. - М.: ФМЛ, 1971.

4. Shoemake, Ken. Animating Rotation with Quaternion Curves. Computer Graphics (SIGGRAPH 85 Proceedings).

5. Shoemake, Ken. Euler Angles Conversions. Graphics Gems IV. Academic Press. www.graphicsgems.com.

6. Watt, Alan, and Mark Watt. Advanced Animation and Rendering Techniques - Theory and Practice. Addison-Wesley, 1992.