Точная табличная модель компонентов ИС для моделирования аналоговых ИС

Белугин С.С. (puerco@mail.ru), Кокин С.А.

ООО Юник Ай Сиз Введение

Непосредственное использование современных компонентных моделей полупроводниковых приборов, например BSIM3, BSIM4 [1,2], для схемотехнического (Spice) моделирования ограничивается вычислительными ресурсами. Альтернативой являются табличные модели компонентов интегральных схем (ИС) [3]. Такие модели состоят из многомерных массивов, в которых хранятся экспериментально полученные точки вольтамперных, вольтфарадных характеристик, и алгоритм их извлечения и обработки.

Известно, что точность табличной модели и гладкость, получаемых характеристик, зависит от алгоритма интерполяции характеристик между узлами таблицы и от числа ячеек таблицы. Как правило, табличные модели применяются для моделирования цифровых ИС, из-за недостаточно высокой точности описания характеристик. С другой стороны за счет своего табличного устройства обеспечивают высокую скорость вычисления значений характеристик по заданным воздействиям, что крайне необходимо для современных программ схемотехнического моделирования.

Точность таблично заданных функций теперь зависит от алгоритма интерполяции функций между узлами таблицы и от числа ячеек таблицы. При реализации алгоритма табличной организации функций модели следует отметить:

1). Требуется большой объем машинной памяти для хранения табличных данных.

2). Получаемые из таблиц характеристики элемента (транзистора) должны перекрывать весь

диапазон изменения входных воздействий, необходимых при моделировании схемы.

3). Алгоритм интерполяции функций между узлами таблицы должен обеспечивать достаточную

точность.

Особенности сплайн интерполяции моделей компонентов ИС

В дальнейшем для простоты ограничимся построением табличной модели, для вычисления статической ВАХ MOП-транзистора. В качестве исходной возьмем модель описанную в [1]. В общем случае выражение для тока канала записывается в виде:

ids = f(vds,vbs,vgs). (1)

ids - ток между стоком и истоком, vgs - разность потенциалов затвора и истока, vbs - разность потенциалов подложки и истока, vds - разность потенциалов стока и истока. Сначала создается таблица значений функции (1) для дискретных значений переменных vdst, vgsj и vbsk. Она представляет собой трехмерный параллелепипед, разбитый по координатам vds, vgs и vbs на ячейки qij. Каждая из них ограничена диапазоном:

vdsx < vds < vdst+1,

vgsj < vgs < vgsj+1, (2)

vbsk < vbs < vbsk+1.

Для получения значения тока ids при произвольных значениях напряжений смещения vds,vgs,vbs, отличных от значений, ограничивающих диапазон текущей ячейки, неизбежно возникает задача интерполяции данных. В случае нескольких переменных и достаточно большого числа точек, глобальная интерполяция, с точки зрения количества выполняемых машинных операций практически не приемлема. Для решения задач локальной интерполяции

зачастую применяется хорошо зарекомендовавший себя алгоритм, основанный на построении кусочно-полиномиальной функции - сплайна.

Рассмотрим сплайн интерполяцию кубическим трехмерным эрмитовым сплайном [4] применительно к таблично заданной функции (1). Таким сплайном называется функция s3j(x,y,z) = s3j3(f;x,y,z), которая в каждом из параллелепипедов f2ij,k = [xu xi+1] х [yu yi+1] x [zu zj+i] (в нашем случае x=vds, y=vgs, z=vbs) имеет вид:

= t(x - x,)r * £ (y - y})r * £(z - zk)), (3)

r=0 r=0 r=0

i - текущий шаг по координате Vds, j - текущий шаг по координате Vgs, k - текущий шаг по координате vbs, ar, b} , crk - коэффициенты сплайна. r=0,1,2,3. Переменные сплайна в текущей ячейке ограничены диапазоном значений (2).

Форма записи сплайна вида (3) содержит 12 неизвестных коэффициентов для каждой ячейки, которые необходимо предварительно вычислить, накладывая на сплайн условия интерполяции. Нам необходимо вычислить коэффициенты a\, bJr, ckr. Используем тот факт, что при фиксированных значениях двух переменных сплайн s3t3(x,y,z) и его первая производная по оставшейся переменной превращаются в одномерные эрмитовы кубические сплайны относительно третьей переменной. Поэтому:

£r,°S (x yq,z) = s,[dr,0f (xp,yq,z);z], r = 0,1;p=i,i+1; q=jj+1. (4)

d -оператор дифференцирования. Формула (4) означает, что производная сплайна равна сплайну производной. Это обстоятельство освобождает нас от необходимости интерполировать функции проводимостей транзистора и его емкостей, поскольку они представляют собой производные функций токов и зарядов. И для получения их значений достаточно будет взять производную соответствующего сплайна в заданной точке.

Таким образом, с помощью (4) из (3) можно вывести четыре одномерных сплайна:

s1jk = a0 + a1*(vds- vds1) + a2*(vds - vds1 )2 + a3*(vds- vds1 )3 (5)

s\ijk = S33[f (vds,vgsj,vbsk);Vds] - сплайн (4) при vgs= vgsj и vbs= vbsk.

S2, jk = b0 + b1* (vds - vds1) + b2* (vds - vds1 )2 + b3* (vds - vds1 )3 (6)

д д

s2jk = rr-S3[f(Vds,Vgsj,Vbsk);vds] = S3 37-f(Vds,Vgsj,Vbsk);vds] - сплайн вида (4) от dvgs dvgs

производной функции (1) при vgs= vgsj и vbs= vbsk.

s3ijk = c 0 + C1* (Vgs - vgs}) + c 2* (Vgs - vgs} )2 + c 3* (Vgs - vgs} )3 (7)

s3ijk = S33[f(vdsi,vgs,vbsk);Vgs]- сплайн (4) при vds= vdsi и vbs= vbsk.

s4jk = d0 + D1* (Vbs - vbsk ) + D2* (Vbs - vbsk )2 + D3* (Vbs - vbsk )3 (8)

s4ijk = S33[f(vdsi,vgsj,Vbs);Vbs] - сплайн (4) при vds= vdsi и vgs= vgsj.

Где a0, a1, a2, a3 - коэффициенты одномерного сплайна slijk, а b0, b1, b2, b3; c0, c1, c2, c3и d0, d1, d2, d3 - коэффициенты одномерных сплайнов s2ijk, s3ijk и s4ijk соответственно. Чтобы

вычислить эти коэффициенты, на каждый одномерный сплайн накладываем следующие условия интерполяции:

\st[f (x), xt ] = f (xt)

S1[f(x) = f (x+1

dSJ f ( x), xi ]

Здесь x - переменная одномерного фиксированные переменные. В случае

f ( x), xt+1] dx

сплайна, а (6) f ( x)

f( x,+1)

f(x) = f(x,y,r)

df (x, y г)

где y,z оставшиеся две

s1 [f (x), x] - один из сплайнов,

представленных в (5) - (8). После решения системы (9) для каждого одномерного сплайна находятся соответствующие ему коэффициенты. После подстановки их в (5)- (8) можно выделить 12 уравнений для 12 искомых коэффициентов a\, b1

\a0 * b0* c0 = A0

r 1 r

a1* b0* c0 = la 2* b0* c0 a3* b0* c0:

b1* c0 * a0 b1* c0 * a1 = a2 * b1* c0

l a0* b2* c0

a0 * b3 * c0

a0* b0* c1 = a0* b0* c2 a0* b0* c3:

= 2 = 3 b0 b1 b2 --c 2

--d 2

(10)

Система (10) является нелинейной. Проведенные исследования показали, что применение метода Ньютона и прочих итерационных методов решения нелинейных систем в нашем случае крайне не желательно, поскольку решение зависит от удачного выбора начальных условий и может расходиться. Более того, на практике система (10) зачастую является вырожденной. Для нас важно гарантированно получить точное решение. Этого можно добиться только выводом аналитических формул для неизвестных системы (10). Для этого коэффициенты a0 и b0 зададим равными 1, и после подстановки в (10) найдем остальные коэффициенты. Правильность решения от этого не пострадает, поскольку все 12 равенств в (10) будут выполняться. Систему (10) можно назвать условиями интерполяции, определяемыми расчетом одномерных сплайнов вида 5 - 8. В таком способе расчета коэффициентов возникает опасность деления на ноль. При a0=0 c0=0, а при определении остальных коэффициентов происходит деление на с0. Эту проблему можно избежать, проанализировав интерполируемую функцию.

Из (5) и (9) следует, что a0 = f(vdsi,vbsj,vgsk). Функция канального тока такова, что точному нулю она равняется при vds = 0, при этом vgs и vbs могут принимать любые значения. В этой точке при фиксированном и равном нулю vds сплайны (7) и (8) тоже равны нулю, поскольку в общем случае они заменяют функцию канального тока. Тогда коэффициенты этих сплайнов с и d можно обнулить. Для решения системы (10) в этом случае приравняем b0 и с0 единице, тогда a0=0. Неизвестные коэффициенты, которые получаются посредством деления правых частей на a0, тоже можно обнулить, поскольку в правых частях этих уравнений стоят нулевые коэффициенты c и d. На рис.1 представлена интерполяция функции канального тока.

231 mv j spline л Ids

391 mv VdS, V

Рис 1. Интерполяция канального тока сплайном вида (3) (увеличенный участок ВАХ)

На рис.1 видно, что сплайн не плотно прилегает к функции. Максимальная относительная погрешность сплайн-интерполяции достигает 3.1 %.

dlds/dVgs, 1/Ohm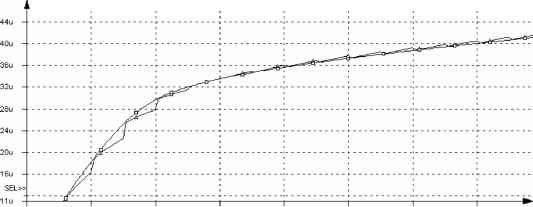

0v 0.2v

□ dlds/dVgs i dSpline/dVgs

Vds, V

Рис. 2. Производные сплайна и функции по vgs.

На рис.2 показаны графики проводимостей. Гладкая линия - это аналитическая производная функции канального тока. Зубчатая линия - производная сплайна функции канального тока. Из проведенного эксперимента видно, что точность интерполяции функции приемлема. По крайней мере, ее можно улучшить, увеличив число ячеек. Но получаемая от сплайна производная значительно отличается от реальной, и это видно даже не вооруженным глазом. Для поставленной задачи такое решение не приемлемо. Поскольку производные тока являются важными величинами для схемотехнического моделирования. Можно конечно принять решение отдельно интерполировать каждую производную функции канального тока. Их всего три. Таким образом, количество таблиц, а соответственно и отводимой для них машинной памяти увеличится в 4 раза. Следовательно, можно сделать вывод, что стандартный способ определения коэффициентов сплайна для поставленной задачи не подходит. Он не может обеспечить высокую точность одновременно функции и ее трех частных производных без значительных затрат вычислительных ресурсов.

Вычисление коэффициентов

Проанализировав способ интерполяции, описанный выше, можно объяснить плохую точность по производным сплайна. Рассмотрим подробнее правые части уравнений в системе

(10). Они находятся посредством решения системы (9) для каждого одномерного сплайна. На примере сплайна (5) решим эту систему. [ a0 = f (vds, ,vgsj ,vbsk)

A0 + A1* (yds,+1 - vdsx) + A2* (vds,+1 - vds, )2 + A3* (vds,+1 - vds, )3 = f (vds,+1, vgsj, vbsk) df (vds1 ,vgs} ,vbsk)

a1 =

dvds

2 df (vds,+1,vgs, ,vbsk) dvds

Из решения видно, что a0 отвечает за равенство сплайна и функции в точке (vds ,vgsj,vbsk),

al отвечает за равенство производной сплайна по vds и производной функции по vds в точке (Vdsi,vgsj,vbsk), a2 косвенно отвечает за равенство производных в конечной точке отрезка

(vdsi+1, vgs j ,vbsk) по координате Vds, и a3 отвечает за оставшееся условие интерполяции, то

есть за равенство функции и сплайна в конечной точке отрезка (vds1+1,vgsj,vbsk) . По аналогии

такие же выводы можно сделать и для коэффициентов B, c, d.

В системе (10) нет уравнений для коэффициентов b3, c0, cl, d0. Следовательно, не будет выполняться равенство производной функции по vgs и производной сплайна в точке (vdst+1, vgs j ,vbsk ) . Отсюда и следуют сильные расхождения графиков производных функции и

сплайна. Проблему можно решить удачным выбором уравнений в (10), но следует отметить, что уравнений всего 12 и какие то из условий учесть все равно не получится.

Определимся с необходимым количеством выполняемых условий для обеспечения достаточной точности интерполяции функции и её производных. В текущей ячейке известны значения функции и её производных по всем трем координатам в восьми точках, ограничивающих ячейку. Из рисунка 1 видно, что наличие в системе уравнений для всех 4 коэффициентов а обеспечило хорошую точность интерполяции функции по координате Vds. Отсюда следует вывод, что наличие всех 32 коэффициентов a,b,c и d в системе (10) позволит обеспечить достаточную точность интерполяции функции и ее первых производных. Так как на концах отрезка по одной из координат сплайн и функция точно равны и равны тангенсы углов наклона касательных к ним, сплайн будет максимально прижиматься к функции на всех промежуточных значениях отрезка, тем самым, обеспечивая и приближение своей производной к производной функции. Если обеспечить такие условия на всех отрезках, ограничивающих ячейку, то точность интерполяции значительно увеличится.

Для этого необходимо наличие еще 20 уравнений в системе (10), рассчитанной всего на 12 неизвестных коэффициентов сплайна (3). Естественно, что 12 неизвестных не смогут обеспечить одновременное выполнение 32 уравнений.

Для обеспечения выполнения всех 32 условий можно воспользоваться раскрытием скобок в кубическом трехмерном сплайне, тогда получится 64 неизвестных коэффициента. Потребуется изыскание дополнительных условий интерполяции - условий равенства вторых производных сплайна и функции и т.д. Дополнительные условия хоть и повышают точность, но при этом значительно усложняют задачу, увеличивая вычислительные затраты для расчета коэффициентов сплайна. Поэтому, предложенный способ повышения точности интерполяции рекомендуется применять только для задач, где требуется высокая точность интерполяции функции и ее производных до второго порядка включительно. Например, для современных средств радиочастотного анализа такая величина, как вторая производная функции канального тока, имеет важное физическое значение. Для задач временной верификации схем достаточно высокой точности интерполяции функции и ее первых производных. Такая точность вполне может быть обеспечена квадратичным трехмерным сплайном, коэффициенты которого рассчитываются новым способом, описанным ниже.

В соответствии с определением, приведенным в [4] и по аналогии с выражением (3) квадратичный трехмерный сплайн имеет вид:

= £ а' (vds - vds,)r * £ ъ\(vgs - vgsj)r * £ ckr(vbs - vbsk )r, (11)

r=0 r=0 r=0

i - текущий шаг по координате vds, j - текущий шаг по координате Vgs, k - текущий шаг по координате Vbs, ar, b} , crk - коэффициенты сплайна. r=0,1,2. Переменные сплайна ограничены условиями (2). В такой форме записи сплайна содержится 9 неизвестных коэффициентов, которые необходимо вычислить, составив систему уравнений из условий интерполяции. Понятно, что для выполнения 32 условий их явно не достаточно. В связи с этим предлагается, раскрыв скобки в (11), привести сплайн к формуле содержащей 27 неизвестных коэффициентов.

s2 3jk = c0 + c1 y + c2 y2 + c3 x + c4 xy + c5 xy2 + c6 x2 + c7 x2y + c8 x2y2 + c9 z +

c10 yz + c11 y2 z + c12 xz + c13 xyz + c14 xy2 z + c15 x2 z + c16 x2yz + c17 x2y2 z + c18 z2 + (12)

c19 yz2 + c20 y2 z2 + c21 xz2 + c22 xyz2 + c23 x2 z2 + c24 x2yz2 + c25 x2y2 z2 + c26 xy2 z2

Здесь: x = vds - vds, y = vgs - vgsj, z = vbs - vbsk.

К положительным свойствам такой формы записи сплайна относится большое число неизвестных коэффициентов, для которых можно подобрать соответствующие условия интерполяции. Конечно, 32 уравнения составить не удастся. Но, если исследовать все возможные способы расчета 27 коэффициентов, можно найти подходящий способ, обеспечивающий точность приемлемую для задач схемотехнического проектирования.

К отрицательным свойствам сплайна (12) следует отнести большие затраты памяти для хранения коэффициентов и процессорного времени для вычисления самого сплайна по сравнению со сплайном вида (3). Процессорные затраты можно сократить уменьшением числа машинных операций для расчета формулы (12). Это достигается с помощью простейших математических преобразований формулы, таких как, например вынесение за скобки общего члена некоторого числа произведений. Затраты памяти тоже можно сократить. Для этого следует модернизировать алгоритм организации данных табличной модели и доступа к ним в машинной памяти. В современных условиях постоянного удешевления машинной памяти приоритетной становится задача повышения точности за счет увеличения числа коэффициентов сплайна.

После проведенных исследований были найдены уравнения, подходящие для вычисления 27 коэффициентов в (12). Более того, подобранные уравнения позволяют определять неизвестные систем аналитическим способом, не прибегая к различным алгоритмам решения СЛАУ, вносящим дополнительную погрешность в решение. Погрешность определения неизвестных коэффициентов благодаря такому подходу соизмеряется с погрешностью машинного округления, возникающей при делении в алгебраических выражениях. Из этих уравнений составляются следующие четыре системы: = cf(vds, vgsj, vbsk )

1 dvdsdvgs

, 2 Cf (vds , vbsk )

cvds (13)

, 2 vgsj ,vbbsk)

c4 hx+c7 hx =--c,

cvgs

c4 hxhy+ c5 hxhy2 + c7 hx2hy+c8 hx2hy2 = f (ydsi+1, vgsj+1, vbsk ) - c0 - c1 hy - c2 hy2 - c3 hx - c6 hx2

df (vds ,vgsj ,vbsk)

dvgsdvbs

, , 2 df(vds,Vgsj+1,vbsk)

10 11 dvbs 9 (14)

, , 2 df(vds,Vgsj ,Vb4+1)

c10 hz+c19 hz =----c1

10 19 1

dvgs

[cw hyhz+ cu hy-hz+cw hyhl + c2{) hfhz2 = f(vds, vgs+1,vbs+1) - C0 - C1 hy-c2 hy2 - c9 hz- hz2

C12 =

df(vds, vgsj, vbsk ) dvdsdvbs

h h2 =dfvgsj, vbsk ) -

< 12 15 dvbs 9 (15)

, 2 df(vds, vgsj, vbsk+d

c12 hz+c21 hz =-T-:--С3

dvds

c12 hxhz+ c15 hx2hz+c21 hxhz + c23 hx2hz2 = f (vds+1, vgsj, vbsk+1) - c0 - c3 hx-c6 hx2 - c9 hz-c18 hz2

(16)

= df (vdsi, vgsj, vbsk) = df (vdsi, vgsj, vbsk) 13 dvdsdvgsdvbs 13 dvdsdvgsdvbs

h h 2 df(vds<,vgsj+l,vbsk)

dvdsdvbs

2 df (vdsi41 ,vgsj,vbsk) c л 1 hx 1 се hx - c л /\

dvgsdvbs

df(vd

c13 hz + c22 hz

df (vds vgsj, vbsk+1)

dvdsdvgs

df (vdsi+1- vgsi+1- vbsk)

c13 hxhy + c14 hxhy2 + c16 hx2hy + c17 hx2hy2 =-----k- c9 - c10 hy - c11 hy2 - c12 hx - c15 hx2

dvbs

h h j 2 h h h 2 ,2,2 df (vdsi+1, vgsj> vbsk +1) h ,2 h ,2

c13 h hz + c16 h hz+ c22 h hz + c24 h hz = - c1 - c4 h - c7 h - c10 hz- c19 hz

dvgs

c13 hyhz + c14 hy2hz + c22 hyhz2 + c26 hy2hz2 = df(-1 g J+1-k+1j) - c3 - c4 hy - c5 hy2 - c12 hz - c21 hz2

dvds

c13 hxhyhz + c14 hxhy2hz + c16 hx2hyhz + c22 hxhyhz2 + c17 hx2hy2hz + c24 hx2hyhz2 + c26 hxhy2hz2 +

+ c25 hx2hy2hz2 = f (vdsM,vgsj+1;vbsk+1) - c0 - c1 hy - c2 hy2 - c3 hx - c4 hxhy - c5 hxhy2 - c6 hx2 -

- c7 hx2hy - c8 hx2hy2 - c9 hz - c10 hyhz - c11 hy2hz - c12 hxhz - c15 hx2hz - c18 hz2 - c19 hyhz2 - c20 hy2hz2

-c21 hxhz2 -c23 hx2hz2

Вместо линейно зависимых уравнений равенства производных сплайна и функции по одной координате использованы условия равенства смешанных производных сплайна и функции по двум координатам в определенных точках. С помощью смешанной производной сплайна максимально приближенной к аналогичной производной функции в начальных точках ячейки сплайну будет задано направление, приближающее его поверхность к поверхности трехмерной функции, которую он интерполирует.

SEL>4 9BuA

1.2v

1 5v

18v Vds.V1

0.9v 1.0v 1.1 v

□ Spline д Ids

Рис.3 Интерполяция сплайном (12) c новым способом расчета коэффициентов. Максимальная

погрешность 0.7%.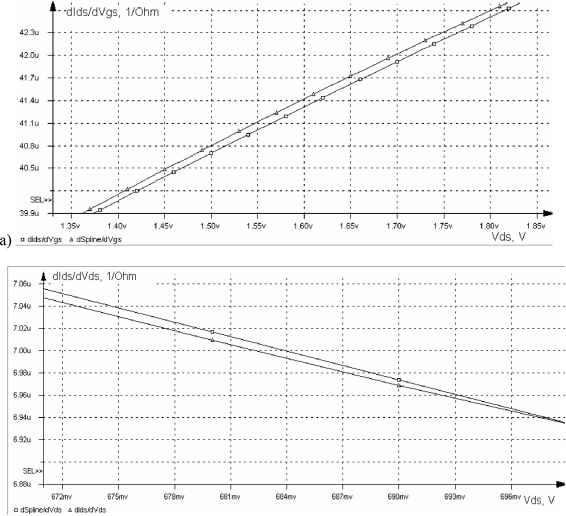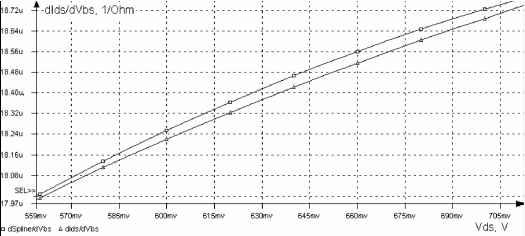

Рис.4 Интерполяция производных.

а) По vgs с максимальной погрешностью 0.1%.

б) По vds с максимальной погрешностью 0.23%.

в) По vbs с максимальной погрешностью 0.27%.

Оценивая относительную погрешность интерполяции производных и функции можно сказать, что полученный сплайн вполне может быть использован вместо функции канального тока, а его производные вместо производных ВАХ.

Оценим теперь выигрыш в вычислительной производительности для программы моделирования при использовании вместо функции канального тока сплайна, интерполирующего ее в некотором диапазоне. Для эксперимента была создана таблица со значениями ids = f(vds,vbs,vgs) и ее производных, необходимых для расчета коэффициентов сплайна. Таблица однородно разбита на 1200 ячеек с шагом разбиения по vds и vgs - 0.1в, по vbs 1в и покрывает диапазон:

0В < vds < 4В, 1В < vgs < 4В, 0В < vbs < 1В.

В каждой ячейке таблицы были вычислены коэффициенты сплайна (12) по системам (13) - (16). Сплайн, рассчитываемый по полученным коэффициентам, использовался в программе моделирования AVOCAD вместо функции канального тока. И для эксперимента было проведено моделирование ВАХ транзистора на диапазоне, покрываемом заданной таблицей.

С помощью программы Intel® Vtune Performance Analyzer 6.0 произведены замеры среднего времени, затраченного процессором на вычисление функции канального тока и ее производных. Для оригинальной функции ids = f(vds,vbs,vgs) это время составило 0,010663 мксек. Для сплайна - 0,001178 мксек. Таким образом, использование сплайна вместо функции канального тока позволило сократить время вычисления ВАХ в 9.05 раз. Результаты по оценкам точности представлены на рис.3, 4.

Для повышения производительности схемотехнического моделирования аналоговых ИС можно использовать табличные модели компонентов (транзисторов). В такой модели вместо дорогостоящих, с точки зрения вычислений, формул для определения значений токов и производных, оказывается, удобно хранить их табличные значения в узлах многомерной сетки с алгоритмом локальной сплайн-интерполяции. Проведенные исследования показали, что стандартные способы локальной сплайн-интерполяции не подходят для решения поставленной задачи. В модели важно получить точное значение не только таблично заданной функции, но и ее первых производных. Этого можно добиться увеличением условий интерполяции, а соответственно и коэффициентов интерполирующего многочлена - сплайна. Условия интерполяции можно выбрать такими, что одновременно:

- повышается точность интерполяции

- реально существует возможность получения точных значений коэффициентов. Существует группа условий, которая позволяет найти коэффициенты аналитическим способом, не прибегая к решению СЛАУ численными алгоритмами. Использование уравнений (13) - (16) позволяет добиться приемлемой, для задач схемотехнического моделирования, точности интерполяции.

Литература

1. Cheng Y., Ш С. MOSFET modeling & BSIM3 users guide. -Kluwer Academic Publishers,1999.

2. Weidong Liu, Xiaodong Jin, Kanyu M. Cao, Chenming Hu BSIM4.0.0 MOSFET Model -Users Manual. http: www-device.eecs.berkeley.edu/bsim3/~bsim4.html 2001.

3. D. Nadezhin, S. Gavrilov, A. Glebov, Y. Egorov, V. Zolotov, D. Blaauw, R. Panda, M. Becer, A. Ardelea3, A. Patel SOI transistor model for fast transient simulation iccad03, November 1113, 2003, San Jose, California, USA.

4. Ю.С.Завьялов, Б.И.Квасов, В.Л.Мирошниченко Методы сплайн-функций. -М.:Наука, 1980, 352с.