Математическое моделирование магнитострикционных преобразователей положения на базе DSP микропроцессора

Вдовин А. Ю. (8atlant8@mail.ru)

Астраханский государственный технический университет

Целю данной работы является построение математической модели магнитострикционного преобразователя положения (МПП) и исследование с ее помощью метрологических характеристик преобразователя.

Структурная схема МПП на базе DSP микропроцессора и осциллограммы сигналов первичного преобразователя представлены на рис. 1.

3 °

& 3

s ю

и &

ФИТЗ - формирователь импульса тока записи; ПУ - предварительный усилитель; ФНЧ - антиэллайсинговый фильтр низких частот; АЦП - быстродействующий АЦП; CLK - тактовый вход АЦП.

Г ВЭВкНг -=ff--1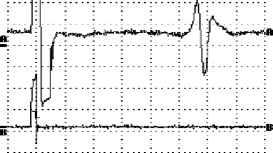

Н- S U g 5 IPig: Ы L В- 1 U

Рис 1. Конструкция МПП (а) и осциллограмма формирующихся сигналов первичного

преобразователя (б).

Устройство работает следующим образом: DSP микропроцессор выдает сигнал на формирователь импульса тока записи ФТИЗ, который формирует мощный импульс тока (рис. 1б, канал В) в первичный преобразователь, представляющий собой магнитострикционную линию задержки на крутильных или продольных колебаниях [1]. В результате электроакустических преобразований на его выходе формируется сигнал считывания, который усиливается по амплитуде предварительным усилителем ПУ (рис. 1б, канал А справа). Антиэллайсинговый фильтр низких частот ФНЧ подавляет частоты выше частоты дискретизации fT для избежания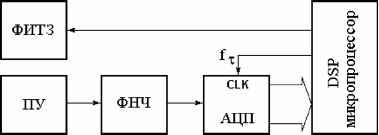

эффекта наложения спектров. Быстродействующий АЦП, непрерывно тактируемый DSP микропроцессором, формирует на его шине данных последовательности цифровых отсчетов соответствующих текущему состоянию сигнала с первичного преобразователя. Алгоритм функционирования DSP микропроцессора производит дальнейшую обработку отсчетов и формирует результат измерения. Результатом измерения является определенный интервал времени между сигналами записи и считывания, который связан с положением объекта позиционирования через скорость распространения магнитострикционного импульса в первичном преобразователе [1].

Блок-схема алгоритма функционирования DSP микропроцессора представлена на рис. 2.

©

Нет

Фиксация времени ид ентнфикацнн полезного сигнала м г I I

Завершение формирования циклического массива

Выделение выборки временного окна

I Конец I

Рис. 2. Блок-схема алгоритма функционирования DSP микропроцессора.

В основу алгоритма функционирования DSP микропроцессора положен разработанный автором метод уменьшения случайной погрешности на основе спектрального анализа сигнала считывания первичного преобразователя.

Поступающие на шину данных отсчеты помещаются в циклический массив. Величина массива должна быть несколько больше требуемой величины соответствующей временному окну изменения сигнала считывания на максимально возможную ошибку времени идентификации полезного сигнала. Величина окна определяет частотное разрешение дискретного преобразования Фурье (ДПФ). Одновременно поступающие отсчеты исследуются алгоритмом идентификации

полезного сигнала. При совпадении условий, которые определяют совокупность поступающих отсчетов как полезный сигнал, фиксируется время поступления отсчета (или его номер) ол. Идентификация промаха, который может возникнуть при мощной помехе, не останавливает циклы заполнения массива. Далее идет завершение формирования циклического массива, заключающееся в проведении еще некоторого количества отсчетов соответствующего окончанию изменения сигнала. Из полученного массива производится выборка отсчетов, величина которой определяется временным окном. По полученной таким образом дискретной последовательности вычисляются коэффициенты ДПФ соответствующие стабильным гармоническим компонентам сигнала считывания, определенных априорно. После этого решается задача восстановления дискретной последовательности, причем восстановление может происходить с шагом меньшим шага дискретизации. Это будет определяться, следующей после, процедурой локализации главного экстремума, заключающая в определении окрестности, где значение восстановленной функции минимально (максимально) кратной шагу дискретизации сигнала. Задача поиска главного экстремума сводится к интерполяции восстановленной функции в этой окрестности и определению ее минимального (максимального) значения.

Для анализа метрологических характеристик преобразователя была реализована его математическая модель в интегрированной инженерной среде MATLAB 6.1 в виде М-файла[2]. Модель способна обрабатывать как искусственно генерированные ею сигналы, так и экспериментальные данные сигнала считывания.

Блок-схема модели представлена на рис. 3

Генератор сигнала

первичного преобразователя

Генератор шума и помех

идентификации

полезного сигналя

Формирователь массива данных

Преобразователь БПФ

Блок обратного ДПФ

Блок локалшации и поиска главного экстремума

Рис. 3. Блок-схема математической модели МПП на базе DSP микропроцессора.

Оцифрованный и отфильтрованный сигнал считывания моделируется при помощи генератора сигнала первичного преобразователя и генератора шума и помех.

Генератор сигнала первичного преобразователя загружает данные из внешних файлов формата ASCII, представляющих собой последовательности чисел - абсцисс и ординат цифровых осциллограмм. Поскольку цифровые осциллограммы несут информацию только о полезном, снятом лабораторно сигнале, полученные данные дополняются нулевыми точками на требуемый временной отрезок. График исходного сигнала представлен на рис. 4.

File Edit View Insert Tools Window Help

ld*belfira 0

Initial sygnal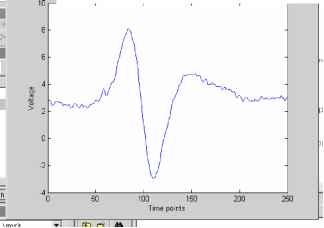

1*1 i-k I л

Рис. 4. График исходного сигнала.

Генератор шума и помех накладывает на основной сигнал три вида распределенных по равномерному закону помех. Это высокочастотный низко-амплитудный шум (0-3,5 В), импульсная помеха большой амплитуды равной сигналу (8 В), которая накладывается на интервале от нуля до прихода полезного сигнала и импульсная помеха (2 В) на интервале изменения полезного сигнала (рис. 5.).

The extended-time sygnal + noise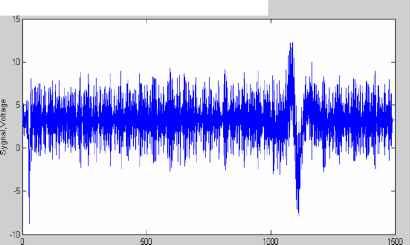

Time points

Рис. 5. График генерированного сигнала

Блок идентификации полезного сигнала работает по алгоритму, основанному на частотных свойствах сигнала. На основании поступающих данных рассчитывается амплитуда основной гармоники сигнала считывания. Как только ее значение превышает некоторый пороговый предел, идентифицируется полезный сигнал. Это делает устройство нечувствительным к шумам и импульсным помехам большой амплитуды.

Формирователь массива данных формирует массив необходимый для идентификации сигнала и массив соответствующий полезному сигналу, определенному блоком идентификации.

Преобразователь БПФ реализует процедуру быстрого преобразования Фурье для массивов идентификации и полезного сигнала. Результат преобразования выводится на график (рис. 6.).

Figure Mo. 3

File Edit View Insert Tools Window Help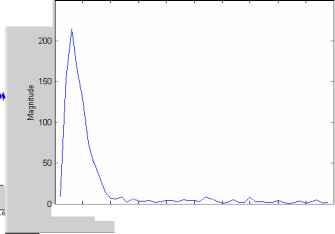

□ 0 02 0 04 0 06 DOB 01 0 12 0 14 0 16 □ 18 02 Frequensy

?7-roF-?nflF m-?s

Рис. 6. Дискретный амплитудный спектр идентифицированного сигнала.

Блок обратного БПФ восстанавливает сигнал по стабильным гармоническим компонентам. На рис. 7. представлены графики выделенного блоком идентификации и восстановленного блоком обратного БПФ сигналов считывания.

Chosen and restored signals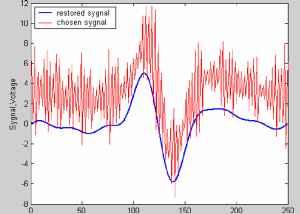

100 150

Time points

Рис. 7. Графики выделенного

и восстановленного сигналов

Блок локализации и поиска главного экстремума определяет минимальные значения функций зашумленного и восстановленного сигнала.

Для анализа влияния помех и шума на результат преобразования положения в качестве исходного сигнала использовалась осциллограмма сигнала считывания. Далее после обработки генераторами сигнала и шума моделировались различные мощные импульсные помехи, распределенные по временной оси случайным образом. Значения амплитуд шумов задавались до величины 3,5 В, что составляет около 40% амплитуды полезного сигнала (рис. 5).

Для оценки уменьшения случайной погрешности при использовании предложенных алгоритмов, проводилась серия экспериментов, в ходе которой были получены осциллограммы сигналов считывания и результаты преобразования положения методом аналогового выделения экстремума с последующим аналого-цифровым преобразованием время-код. Измерения проводились в конце 5-и метрового диапазона, где случайная погрешность имеет максимальное значение. Полученные осциллограммы были обработаны разработанной моделью.

На рис. 8а и рис. 8б приведены графики результатов исследований влияния шума и импульсных помех большой амплитуды и графики оценки уменьшения случайной погрешности. Для сравнительного анализа приведены результаты преобразования с аналоговым методом

выделения экстремума (при исследовании влияния шума и импульсных помех большой мощности оценивались пиковые значения сигнала считывания, поскольку аналоговые методы оказываются неработоспособны для данных уровней шумов):

Error diagrams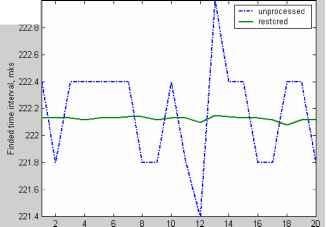

10 12 14 Number of experiment

а) График измерений пиков исходного зашумленного и обработанного сигналов

Рис. 8. Графики исследований влияний шумов погрешности.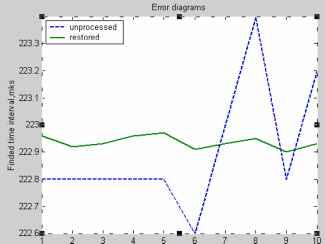

Number of experiments

б) График оценки уменьшения случайной погрешности в конце 5-метрового диапазона

и помех и оценки уменьшения случайной

Как видно из графика разброс пиков зашумленного сигнала составляет ±1,2 мкс, что составляет погрешность ±3,6 мм для датчика на крутильных колебаниях. Разброс минимумов восстановленного сигнала составляет ±20 нс, что соответствует погрешности ±0,06 мм. Кроме этого, применение алгоритмов позволяет получить метрологически надежный результат вследствие частотной идентификации сигнала.

Из графика оценки уменьшения случайной погрешности видно, что максимальный разброс измерений, выделение сигнала в которых проводилось аналоговыми методами, составляет ±400 нс, разброс измерений в результате обработки разработанными алгоритмами, реализованных в имитационной модели составляет ±30 нс. Таким образом, уменьшение случайной погрешности составляет более 90%.

Основные результаты и выводы:

1. Разработана математическая модель МПП на базе DSP микропроцессора, реализующего метод уменьшения случайной погрешности на основе спектрального анализа сигнала считывания первичного преобразователя.

2. Предложенная модель способна обрабатывать экспериментальные данные, что делает ее применимой для исследований МПП.

3. Математическое моделирование МПП позволяет оценить уровень его помехоустойчивости и случайную погрешность.

Работа выполнена по гранту РФФИ № 05-01-96508-р поволжье а Математическое моделирование магнитострикционных преобразователей

Литература

1. Надеев А. И. Магнитострикционные интеллектуальные преобразователи параметров движения. Монография /Астрахан. гос. техн. ун-т.-Астрахань, АГТУ, 1999. - 155 с.-деп. в ВИНИТИ 22.07.99. № 2385 - В99.

2. Кетков Ю. Л., Кетков А. Ю., Шульц М. М. MATLAB 6.x.: программирование численных методов. - СПб.: БХВ-Петербург, 2004. - 672 с.: ил.

3. Л. Рабинер, Б. Гоулд Теория и применение цифровой обработки сигналов под редакцией Ю.Н. Александрова: - М.: Мир , 1978. - 848 с.: ил.