Численное исследование влияния параметра замагниченности на динамику плазменной перемычки

Кингсепп А.С. (2), Коваленко И.В. (1), Лобанов А.И. (1), Пахомов Ю.И. (jp@cs.mipt.ru ) (1)

(1) Московский физико-технический институт (государственный университет),

(2) РНЦ Курчатовский институт

В ходе экспериментального изучения динамики высокотемпературной плазмы в плазменных переключателях тока (111 ГГ) существенную роль играет характер проникновения магнитного поля в плазму, так как от напряженности поля зависит коэффициент теплопроводности, и, следовательно, выход тепла на конвертор. Для теоретического исследования протекающих при этом процессов широко применяется численное моделирование.

В ряде теоретических и экспериментальных работ было показано, что в режиме электронной магнитной гидродинамики [1] (когда эффект Холла существенен) поле быстрее проникает в плазму вдоль анода. Образующиеся при ЭМГ-диффузии магнитного поля токовые петли могут приводить к локальному нагреву плазмы и повышению давления вблизи анода - так называемому анодному взрыву .

Процессы, протекающие в установках класса Стенд-300 , характеризуются значительными перемещениями плазменной перемычки, сильными ее деформациями. 1роведенные ранее расчеты свидетельствуют о сильной зависимости динамики оболочки от начального нагрева плазмы [2]. Отметим также, что существенной чертой изучаемых процессов является наличие многих видов неустойчивостей плазмы, прежде всего неустойчивости Рэлея - Гейлора. В связи с этим интерес представляют многомерные (двух- и трехмерные) численные эксперименты.

1ри температурах и плотностях, характерных для экспериментов на установке С-300 и в расчетах, могут проявиться и эффекты электронной магнитной гидродинамики (ЭМГ). Специального рассмотрения требуют также эффекты, связанные с проявлениями ЭМГ неустойчивостей, а также поправки ЭМГ, влияющие на характер проникновения магнитного поля.

Для расчета течений, характеризующихся большими сдвиговыми деформациями, чаще всего применяются разностные методы, основанные на явной аппроксимации уравнений на подвижной (лагранжевой) сетке. Основным недостатком данных методов является нарушение

рис. 1.

Физическая

установки Стенд-300

однородности расчетов, связанная с необходимостью избежать выворачивания ячеек. Чаще всего для предотвращения выворачивания применяется пересчет на новую сетку с интерполяцией значений. Кроме того, явные численные методы всегда имеют достаточно сильные ограничения на шаги по времени, связанные с условием устойчивости Куранта. Неявные разностные схемы обладают большим запасом по устойчивости и могут оказаться свободными от некоторых недостатков явных схем.

В данной работе предложен подход к построению неявного метода для решения уравнений МГД. Метод расчета основан на вариационном способе построения разностных схем для уравнений механики сплошной среды [3-5]. Похожие неявные методы ранее реализовывались для задач однотемпературной МГД [6]. Характерной особенностью предлагаемой разностной схемы является естественное разделение электронной и ионной энергии. Это приводит к расщеплению системы уравнений для определения давления на следующем временном слое на системы для ионного и электронного давлений.

Использованные при моделировании параметры задачи соответствуют одной из экспериментальных установок (Стенд-300 [7-9]), созданной в РНЦ Курчатовский институт .

Постанока задачи. Рассмотрим физическую модель задачи. Плазменный размыкатель тока (установка Стенд 300 ) представляет собой систему из двух коаксиальных проводящих цилиндрических электродов. Электроды подключены к электрической цепи, содержащей генератор импульса тока. Внутри находится полимерная (майларовая) перемычка. Плазма создается в результате электрического пробоя и последующей ионизации материала полимерной пленки [7, 8]. Пренебрегая переходными процессами, можно считать, что сразу после включения тока во внешней цепи материя превращается в плазму. Полагаем далее в расчетах, что плазма однородна по составу и состоит из углерода.

В начальный момент времени плазма занимает пространство между электродами: R1 < r < R2 (рис. 1). Температуры электронов и ионов плазмы Te, Tu в начальный момент времени задаются распределенными по пространству ввиду того, что в эксперименте плазма прогревается предимпульсом тока. Проводимость плазмы о зависит от плотности и температуры. Плотность вещества р в момент времени t = 0 считалась однородной. Постановка задачи аналогична описанной в [2].

Для описания протекающих процессов используется система уравнений магнитной гидродинамики (МГД) с учетом эффектов электронной магнитной гидродинамики (ЭМГ) для переноса магнитного поля. Основные масштабы,

dP + p.{ - d(rVr) 0

dt V r dr dz

dvr j dt p

(1 d ( B2

r dr

4npr

dv J d/ 2 Л

dt p dz

P +-

Addiizeff 6e + J(zeff)) Pe divv + div(Kegrad(Te)) + Q + Qei -p de.

i--- P. divv + div(K. grad(T.)) Q ., A dt 1 i i ei

dB crotE, jrotB, E i(ve xB) +± - CVPe R), dt 4n c a ewe

ne [B xWTe ] R 0.71neV,Te 1.5 I, ,

®eTe \B\

ve v -, Pe WeTe, Q + i(j,R). e ne a e

В приведенных выше формулах индекс e относится к электронам, а i - к ионам. Большинство обозначений традиционны, P без индекса означает полное давление - сумму парциальных давлений электронов и ионов, функция J(zef) учитывает потери энергии на

ионизацию, zef - эффективный заряд иона. B - напряженность магнитного поля, j -

плотность тока, ve - электронная токовая скорость, о - проводимость, ne - концентрация электронов, Te - электронная температура, Q - джоулев нагрев. В дальнейшем считаем, что магнитное поле имеет лишь азимутальную компоненту.

Приведем соотношения, необходимые для замыкания системы. Уравнения состояния:

pTezef

Pe 9.68 -AS. ee 14.4Te,

P 9.68PT-; 6, 14.4T ,

i A i

здесь и далее А - число нуклонов в ядре.

Зависимость эффективного заряда иона от электронной температуры дается выражением

у

zf 9T/3,zff < Z , иначе zff Z , где Z - максимально возможный заряд иона для данного

элемента (материала). Для рассматриваемого далее материала - углерода - Z принимает значение 6.

которые использовались при приведении системы к безразмерной форме записи, выбирались следующими: время [t]=10-7 c, длина [r]=1 см, плотность [р] = 10-3 г/см3, температура (энергия) [T]=1 КэВ. В безразмерном виде в осесимметричной форме используемые уравнения имеют вид:

Для описания потерь на ионизацию применяется скейлинг:

ti ) 0.131

J ( Zeff ) =-27

0.85 + 0.15Z/3

(z 3 2 z \

Zeff + ZJ] + Zeff

6 2 6

Граничные условия. На правой и левой границах области ставились условия непротекания, соответствующие жесткой стенке. На нижней и верхней границе ставились условия границы с вакуумом. При этом азимутальное магнитное поле на нижней границе связано с полным током во внешней электрической цепи известным соотношением, записанным в безразмерных переменных:

0.2/(t) п t

I (t) = 70sin:

R 2Timp

где I - ток во внешней цепи, R - текущий радиус точки нижней границы. В случае учета радиационных потерь на всех границах ставились условие отсутствия падающего извне излучения.

Разностная схема. Для численного решения нелинейной системы применяется консервативная разностная схема на криволинейной подвижной сетке с использованием расщепления по физическим процессам. На первом этапе расчета (модуль МГД) используются уравнения модели движения двухтемпературной плазмы в магнитном поле в приближении МГД. Расчет эволюции магнитного поля проводится на замороженной на данном шаге по времени сетке с применением ЭМГ-системы, в качестве начальных данных используются результаты модуля МГД. На следующем этапе расчета учитываются изменения электронной и ионной температур за счет теплопроводности. На заключительном этапе расщепления проводится коррекция значений температуры, учитывается обмен энергиями за счет электрон-ионных столкновений. Далее процесс расчета повторяется на следующем шаге по времени.

Для построения предлагаемого неявного метода (модуль МГД) использовались: система уравнений двухтемпературной магнитной гидродинамики (МГД), уравнения состояния и условие вмороженности магнитного поля [10].

Примеры расчета динамики в установке Стенд-300 . Результаты моделирования

При рассмотрении этих задач использовались неявные методы решения уравнений МГД на подвижных сетках. Модуль расчетов динамики плазмы на основе неявной схемы реализован в виде нескольких файлов на языке FORTRAN77 для совместного использования с

Для обмена энергиями между электронной и ионной компонентами плазмы имеем Qel = 8.48 101 .

имеющимися программами. В данном модуле для численного решения нелинейной системы применяется консервативная разностная схема на криволинейной подвижной сетке с использованием расщепления по физическим процессам.

Ранее для подобных расчетов использовался модуль МГД, основанный на явной разностной схеме [7, 10]. Применение этого модуля было ограничено в связи с необходимостью устранения численной неустойчивости. Использование неявной схемы в модуле МГД позволило проводить расчеты в более широком диапазоне параметров при сохранении свойств аппроксимации и устойчивости разностной схемы. А также снять существенные ограничения на шаги по времени, диктуемые условиями устойчивости.

Численное моделирование динамики плазмы на Стенде - 300 проводилось при различных значениях параметров плазмы. Приводимые ниже результаты расчетов получены для следующих вариантов модели: радиусы электродов R] = 0,2 см, R2 = 0,5 см, начальная толщина оболочки z2 = 0,075 см, начальная плотность вещества плазмы 0,3 мг/см3, материалом плазмы считался углерод. Длительность импульса электрического тока Timp = 100 нс, амплитуда импульса тока /0 = -1 МА. По предварительным качественным оценкам параметр замагниченности в условиях, соответствующих установке С - 300, находятся в пределах 0,011,0.

В работе также учитывается неравномерное начальное распределение температуры плазмы Te = Ti = T(r). Считается, что в результате прохождения предварительного импульса плазма нагревалась. Так как плотность тока выше в окрестности катода, то начальная температура в этой области выше. Будем считать, что начальное распределение температуры можно описать соотношением:

T(r) T0 +ATexp( (r R1)2 /L2),

где R1 - радиус внутреннего электрода, L - ширина зоны прогрева. Представленные результаты получены при значениях T0 = 2 эВ, AT = 8,5 эВ, L = (R2 - R1)/2.

По данным численных расчетов [10], динамика плазменной перемычки существенно зависит от начального прогрева плазмы, то есть от начального распределения температур.

a) 40 нс б) 45 нс

Рис. 2а Эволюция подвижной лагранжевой сееки 40x15 ячеек.

Так как в расчетах использована подвижная перестраеваемая сетка, по динамике сетки можно восстановить эволюцию плазменной перемычки. Вначале плазма разлеталась под действием газокинетического давления. По мере роста тока генератора начиналось подтормаживание нижней границы, изменялось направление движения перемычки. Плазма приходила в движение при времени 17-20 нс. По мере возрастания тока и нагрева в приэлектродной области по материалу перемычки начинала распространяться ударная волна. На рисунках 2a и 2b показано изменение формы расчетной области при временах 40-50 нс. Видно, что наблюдается активное движение плазменной перемычки как целого, в области ударной волны имеет место сгущение сетки.

Для таких режимов сжатия характерен эффект снежного плуга , когда вещество

концентрируется в достаточно узкой области [11]. Эффект снежного плуга виден на рис. 3, где

приведены распределения плотности (концентрации) в соответствующие моменты времени.

На рис. 4 для того же варианта расчета приведены распределения электронной и ионной температур. В области снежного плуга они практически равны, наблюдается незначительное преобладание электронной температуры. Это связано с джоулевым нагревом.

Вблизи внутреннего электрода (анода) плотность тока максимальна, соответственно, там же наблюдается и максимальное тепловыделение за счет джоулева нагрева. Но в силу большого значения магнитной индукции вблизи анода формируется сильная ударная волна. Из-за наличия в разностной схеме искусственной вязкости [12], фронт ударной волны размазан на несколько ячеек разностной сетки. Формирование ударной волны можно проследить по превышению значений ионной температуры над электронной (рис. 4). Так, для 40 нс. Максимальное значение электронной температуры в области за ударной волной составляет 18,5 эВ, в то время как для ионов температура достигает 27,5 эВ. К 50 нс эта разность увеличивается , и температура электронов достигает 36,4 эВ, а ионов - 86 эВ.

При времени около 50 нс существенно изменяется характер проникновения магнитного

Ниже на рисунках показаны некоторые результаты расчетов:

поля в материал плазмы. Если до этого времени проникновение поля носило диффузионный характер, то в связи с повышением электронной температуры вблизи анода магнитное поле оказывается вытесненным из плазмы (рис. 5). В силу нелинейных эффектов на границе ударной волны вблизи границы с вакуумом формируются токовые петли. После формирования таких петель (а в наших расчетах такие петли являются устойчивыми), магнитное поле начинает распространяться от анода вдоль нижней границы. Видно, что такое распространение уже не носит диффузионный характер, а представляет собой нелинейную волну. Пока остается открытым вопрос о немонотонности магнитного поля вблизи фронта этой волны, возможно, она носит численный характер.

Оценки характерных размеров неоднородности в этом случае указывают на то, что может наблюдаться режим пространственного разделения зарядов, и в окрестности фронта нелинейной волны сформулированная выше математическая модель уже не описывает динамику плазмы.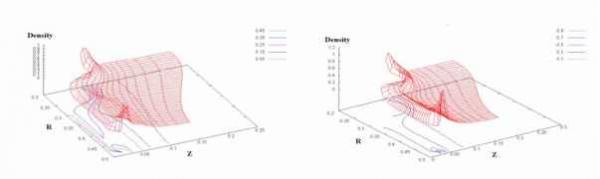

а) 40 нс

б) 45 нс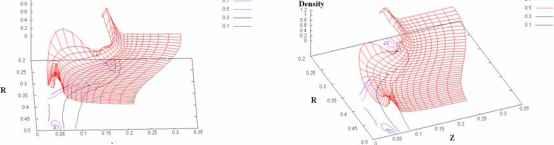

в) 49 нс

г) 50 нс

Рис. 3 Эволюция плотности. Сетка 40x15 лагранжевых ячеек.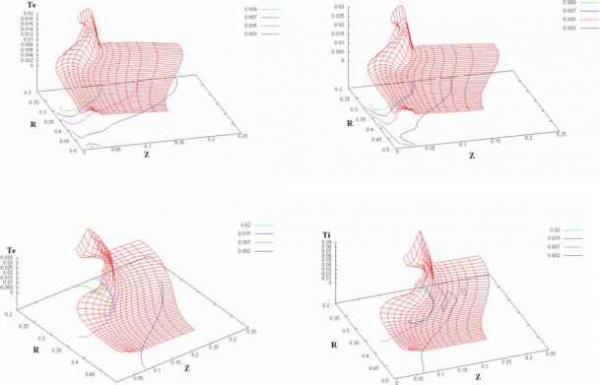

Рис. 4 Распределения электронной и ионной температуры для времен 40 и 49 нс. Сетка 40x15 лагранжевых ячеек.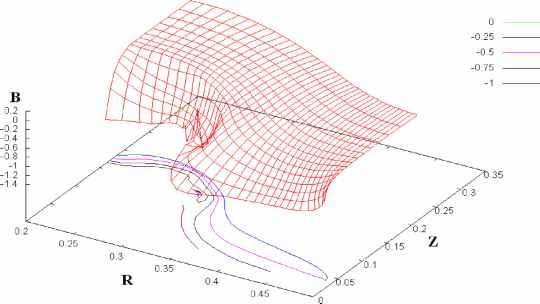

Рис. 5 Распределение магнитной поля. Сетка 40х15 лагранжевых ячеек. Время 50 нс.

Параметр замагниченности (со Be т e) сильно влияет на характер проникновения

магнитного поля в плазму. Напрямую экспериментально его определить невозможно; возможны только косвенные оценки. Ввиду большой погрешности измерений, по некоторым прикидкам значение параметра замагниченности может значительно превышать 1. Таким образом, интерес представляют численные эксперименты по оценке влияния параметра замагниченности на динамику плазмы.

В численном эксперименте значение этого параметра повышалось до 15. При всех значениях параметра замагниченности на небольших временах (до 35 нс) динамика плазмы существенно не отличалась от описанной выше. Для больших времен наблюдались качественные отличия. Наиболее ярко они проявляются при соBeTe 7.

Эволюция плазменной перемычки показана на рис. 7. Мелкомасштабные эффекты при проникновении магнитного поля в материал плазмы и джоулев нагрев в этом случае приводят к формированию пузырей малой плотности с магнитным полем внутри. Теоретически такая возможность проникновения магнитного поля в материал была впервые рассмотрена Л. И. Рудаковым с соавторами [13,14]. В последнее время появились экспериментальные указания на то, что такой характер проникновения возможен, по крайней мере, для Z-пинчей

[15].

Отметим, что в случае формирования пузыря расчетная область становится неодносвязной, что влечет за собой невозможность продолжения счета по используемым разностным схемам на подвижной сетке.

Отметим, что проникновение в материал магнитного поля с образованием малоплотных пузырей приводит к формированию более слабых ударных волн в перемычке. В частности, это видно на рис. 9, где показаны распределения электронной и ионной температур. В то время как характерные значения электронной температуры остались примерно теми же, что и в предыдущем варианте, значение ионной температуры уменьшилось в полтора раза (до 58 эВ).

Как и в предыдущем расчете, вещество скапливалось на нижней границе вдали от анода из-за эффекта снежного плуга (рис.8). Для вариантов с образованием пузырей так же характерна смена типа проникновения магнитного поля в материал плазмы с диффузионного на нелинейную волну. Рассмотрение направления проникновения показывает, что проникновение магнитного поля соответствует направлению распространения волны КМЧ [16].

При дальнейшем увеличении значения параметра замагниченности характер проникновения магнитного поля в материал плазмы вновь менялся, малоплотный пузырь с магнитным полем не формировался. Отличия от вариантов с малой замагниченностью

заключались в изменении амплитуд ударных волн и появлению мелкомасштабных образований в материале плазмы.