Математическое моделирование микроэлектронных частотных датчиков давления

Шикульский М.И. (shikul m@mail.ru )

ФГОУ ВПО Астраханский государственный технический университет

Внедрения в отечественную промышленность новых прогрессивных технологий, которые требуют повышения точности измерений и регулирования параметров технологических процессов. При создании таких систем контроля и регулирования следует ожидать широкого применения резонаторных или частотных датчиков [1].

В частотных датчиках давления вибрационный частотный элемент может быть выполнен в форме миниатюрных силочувствительных балочных резонаторов, может представлять собой колебательную струну, монокристаллическую кремниевую нить, натяжение которой зависит от прогиба диафрагмы, перекладину, опирающуюся на диафрагму, вакуумную полость с кремниевой оболочкой. Наконец, сама мембрана может играть роль резонатора. Чаще всего, в качестве чувствительного элемента в частотном датчике давления используется диафрагма - мембрана с отверстием в центре, по диаметру которого расположена колебательная струна или балка, играющая роль резонатора (рис. 1).

Принцип работы струнных датчиков различных физических величин заключается в

том, что с помощью первичного преобразователя измеряемая физическая величина преобразуется в приращение силы продольного натяжения струны AF, что приводит к изменению частоты колебаний f0 до f. Механические колебания в струне возбуждаются

магнитоэлектрическим способом.

Приращение частоты колебаний

2

Рис. 1 Схема вибрационного микроэлектронного датчика давления

- упругая диафрагма,

- резонатор

струны будет являться мерой измеряемой величины, то есть.

Af = f

1 ±AF

При отсутствии начального натяжения в струне частота колебаний определяется по формуле:

f = f,V1 + KF

где f - частота резонансных колебаний балки в напряженном состоянии;

f0 - частота резонансных колебаний балки при отсутствии в ней силы продольного натяжения (F= 0)

Таким образом, для определения выходной характеристики частотного датчика давления - изменения частоты колебаний - необходимо знать силу натяжения струны резонатора, возникшего под воздействием давления, а также параметры, зависящие от размеров струны и свойств материала.

Сила натяжения пропорциональна напряжениям в точках крепления струны, которое в свою очередь по закону Гука зависит от деформаций диафрагмы.

Для определения силы натяжения струны необходимо знать механические напряжения на поверхности плоской диафрагмы, возникающие под воздействием давления, в точках крепления струны.

Для упрощения будем решать задачу в два этапа: вначале найдем выражения для определения напряжений в плоской пластине без отверстия - мембране, а затем - в плоской пластине с отверстием, то есть диафрагме. После этого можно будет перейти к определению зависимости изменения частоты колебаний резонатора датчика от величины давления, то есть к получению зависимости выходных характеристик преобразователя от входных величин.

Существует аналитический метод определения деформаций в плоской пластине при малых прогибах [2]. Вследствие хрупкости полупроводниковых элементов в микроэлектронных датчиках давления мембрана работает в области малых перемещений. Однако, аналитический метод не позволяет учесть анизотропность свойств материала микроэлектронного датчика давления. В связи с этим, была разработана математическая модель плоской деформации мембраны, учитывающая как анизотропность свойств материала мембраны, так и распределение параметров в радиальном и окружном направлениях [3]. В основу этой модели положена теория энерго-информационных моделей цепей (ЭИМЦ) и аппарат параметрических структурных схемм (ПСС), которые дают возможность не только графически изображать причинно-следственные связи между величинами и параметрами, но и относительно просто получить аналитические зависимости одной величины в функции другой величины [4]. Теория ЭИМЦ унифицирует описание процессов различной физической природы в первичных преобразователях, что позволяет автоматизировать их проектирование.

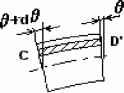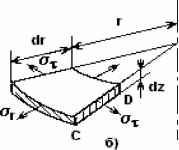Рис 2 Деформации и напряжения в элементе мембраны

1 -м3

(Sr +MSt) (MSr + St )

На ПСС напряжений плоской мембраны под давлением (рис. 3) деформации в радиальном направлении n-го элемента соответствует величина линейного механического заряда Qnumi, а деформации в окружном направлении n-го элемента соответствует величина линейного механического заряда

Так как деформации и напряжения имеют определенную ориентацию на плоскости, то их можно рассматривать как вектора.

Вектор деформации n-го элемента, которому на ПСС соответствует величина линейного механического заряда Qмт равен геометрической сумме линейной и окружной деформации, а вектор напряжения n-го элемента, которому на ПСС соответствует величина линейного механического воздействия Uмлп равен геометрической сумме линейного и окружного воздействия. Вектор напряжения n-го элемента имт равен произведению вектора деформации QMnn на механическую линейную жесткость n-го элемента WMnn. В соответствии с законом Гука для плоского напряженного состояния (3) жесткость n-го элемента WMnn представляет собой матрицу:

Разработку ЭИМЦ преобразователя или его элемента можно разбить на два этапа:

разработка ПСС цепи;

вывод математических зависимостей, выражающих величины и параметры ПСС через реальные физические величины.

Для решения этой задачи рассмотрим элемент плоской пластины, отсеченный двумя осевыми и цилиндрическими сечениями.

Изгибные напряжения в радиальном rjr и окружном rjt направлениях (рис. 2) связаны с деформациями уравнениями закона Гука [1]

W =

млп

Е

1 -м3 1м 1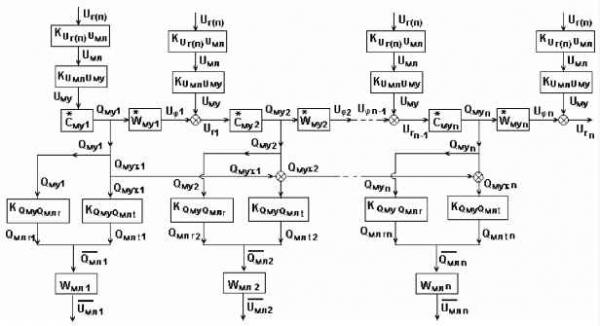

Рис. 3. ПСС напряжений плоской мембраны под давлением

Таким образом, построена ПСС напряжений мембраны и определены математические зависимости, выражающие величины и параметры ПСС через реальные физические величины, то есть, разработана математическая модель деформаций плоской мембраны.

Диафрагма отличается от мембраны наличием отверстия в центре. Для обеспечения достаточной точности математической модели нужно увеличить количество звеньев n так, чтобы на участок радиуса от отверстия до периферии мембраны приходилось не менее 5 звеньев. В то же время в радиусе отверстия должно укладываться целое количество звеньев n0. ПСС диафрагмы идентична ПСС мембраны. Отличие состоит в том, что для диафрагмы последним звеном является звено (n-n0). Нумерация звеньев ведется от периферии к центру.

Следующий этап - разработка ЭИМЦ вибрационного датчика давления. Так как при воздействии усилия на резонатор изменяется частота его колебаний, которая не является ни параметром ПСС, ни величиной, а является аргументов функции величины синусоидального механического заряда (положения колеблющейся точкой), и зависимость эта нелинейная, то теория ЭИМЦ и аппарат ПСС не описывают эти преобразования. В связи с этим, теория ЭИМЦ была дополнена новым понятием - функцией величины, а в

Цг(п)

lUr(n)Uh

Jr(n)

KuunUuy

и

*МЛ Г1,

Jr(n)

Quy2

Ому(П-Пп)

urtn-no)-i

-муп

Qh/yCn-ng)

0uyi2

U(n-n0) Ur<n-nn)

Quyil

Quy2

К3му0мл11

QhyQhi

Quy(n-ng)

Junt2

*МЛ r(n-ng)

Quyi(n rig)

KQuyQn,

WH 2

Онл t(n-n0)

мл(п-по)

WMn(n-n0)

Имл^п-по)

(f = У (Uim))

5мл = (А, f0,cp)

Рис 4. ПСС микроэлектронного частотного датчика давления

Литература

1. Карцев Е.А. Датчики неэлектрических величин на основе унифицированного микромеханического резонатора Приборы и системы управления. 1966. № 4

2. Л. Е. Андреева. Упругие элементы приборов. М.: Машиностроение. 1981, 392с.

3. И. Ю. Петрова, О. М. Шикульская. Универсальная структурно-параметрическая модель плоской мембраны Датчики и системы 2000 №2 - с.14-16

4. Зарипов М. Ф., Петрова И. Ю. Энергоинфориационный метод анализа и синтеза чувствительных элементов систем управления Датчики и системы. 1999 № 5.

аппарат ПСС введены новые обозначения: ромб - для параметра величины, и скругленный прямоугольник - для обозначения нелинейной функции. Это позволило разработать ПСС микроэлектронного частотного датчика давления (рис. 4) и выявить математических зависимостей, выражающих величины и параметры ПСС через реальные физические величины. Введенные в теорию ЭИМЦ дополнения можно использовать для описания колебательных и волновых процессов любой физической природы.