Нелинейная динамика системы связанных автогенераторов, синхронизуемой фазорасщепленным внешним сигналом

Антипов В.Б. (antip@elefot.tsu.ru) (1), Антипов И.Б. (1), Макаров С.Ф. (2)

1. Сибирский физико-технический институт, 2. Томский государственный университет

Введение

Система связанных автогенераторов (АГ), на каждый из которых внешний сигнал действует с определенным фазовым сдвигом, обладает свойством выделять подавленную несущую фазоманипулированного сигнала. Основные свойства стационарных и динамических режимов в системах с произвольным числом автогенераторов N рассмотрены в [1,2]. Установлено, что динамические процессы в системе достаточно адекватно отражаются динамикой векторной суммы колебаний парциальных генераторов, при этом система по поведению аналогична системе ФАП 1 порядка [3] с приведением фазы к сектору шириной 2п / N. Полоса синхронизации системы пропорциональна N-й степени амплитуды внешнего сигнала.

С точки зрения использования системы в фазовом демодуляторе важное значение имеет вопрос о помехоустойчивости такого демодулятора. Непосредственное применение выводов классической теории фазовой синхронизации ограничено сделанными в [2] допущениями о неизменности конфигурации векторов колебаний парциальных АГ. В условиях, когда вслед за переходами фазы обрабатываемого сигнала векторная конфигурация непрерывно перестраивается, указанные выводы могут оказаться некорректными.

Цель данной работы - оценить степень корректности динамической модели рассматриваемой системы и определить помехоустойчивость демодулятора на ее основе.

1. Модель системы связанных автогенераторов

Рассматривается система N взаимно-синхронизованных автогенераторов (АГ), на которую дополнительно воздействует внешний синхронизующий сигнал, подводимый к каждому отдельному АГ с порядковым номером m с фазовым сдвигом 2шп/N . В такой системе могут существовать N стационарных режимов, инвариантных по отношению к скачкам фазы внешнего сигнала на дискреты вида 2ят/N, что позволяет выделять когерентное опорное колебание при приеме ФМ сигналов с подавленной несущей.

= S + ti£sin>m -(pn) + /lsm(# -(pn) 0),

n(2n -1)

где un =- - фаза внешнего сигнала, подводимого к АГ с порядковым номером

n , Л - относительная амплитуда внешнего сигнала, JU - коэффициент амплитудной связи

между АГ, 8 - расстройка частоты внешнего сигнала относительно собственной частоты системы. N стационарных режимов существуют при условии Л < JJN / 2.

При анализе стационарных режимов [1] было предложено воспользоваться геометрическим представлением, ассоциирующим колебания отдельного АГ с единичным вектором ak в плоскости комплексных амплитуд. Уравнения стационарного режима без

расстроек при такой трактовке отражают требование того, чтобы каждый вектор a

располагался вдоль направления, определяемого векторной суммой СТ всех парциальных

колебаний S = a % плюс вектор внешнего воздействия . Суммарный вектор

оказался не менее удобным параметром также и для описания поведения системы в динамическом режиме. Скорость изменения фазы суммарного вектора определяется тремя компонентами: относительной расстройкой частоты внешнего сигнала, внутренними силами, обеспечивающими равновесную конфигурацию векторов, и внешней силой, пропорциональной амплитуде сигнала. Внутренние силы не в состоянии самопроизвольно изменять ориентацию суммарного вектора. В то же время благодаря внутренним силам обеспечивается жесткость векторной конфигурации, проявляющаяся в практически неизменной взаимной ориентации парциальных векторов. Таким образом, динамика системы вполне адекватно отражается поведением суммарного вектора.

Выражение, полученное для внешней силы в отсутствие расстройки, имеет вид

dt T2 +1

juS + Лcos(вn - (S)

Выражение в правой части (2) соответствует периодической функции, близкой к синусоидальной. На интервале 2п функция имеет N периодов. Устойчивым состояниям соответствуют нулевые точки с отрицательной производной. График функции является фазовым портретом системы.

2. Режим с расстройкой как частный случай динамического режима

Уравнения для фаз АГ имеют вид

d(pS = F(x) = MxZ Sm(e -(Ps)-T C0S(e -(Ps) . (3),

dt t: +1

jS + к cos(0n - (ps) 1 + x cos(0n - (ps)

Введение безразмерных переменных делает коэффициент j универсальной мерой

масштаба в рассматриваемой системе: с одной стороны, это мера для относительной амплитуды внешней силы, с другой стороны - мера для относительной скорости переходных процессов. Такого общего представления достаточно для выявления закономерностей динамического поведения системы. Разумеется, на практике связь между амплитудой синхросигнала и скоростью релаксации зависит от особенностей схемной реализации. В конкретных устройствах могут существовать режимы с теми или иными величинами амплитуд, связей, параметров нелинейности активных элементов, добротностей контуров и т. п. Вместе с тем, насколько решенной в радиотехнике можно считать задачу о взаимной синхронизации, настолько в данных рассуждениях допустимо абстрагирование от конкретных деталей.

Перейдем к динамике системы при ненулевой расстройке частоты внешнего сигнала относительно собственной частоты колебаний. Интуитивно мы можем представить ситуацию с расстройкой как наличие в правой части уравнения (2) слагаемого, отвечающего за указанную расстройку 8 и пропорционального ей. Это слагаемое приводит к сдвигу фазового портрета по оси ординат в положительную или отрицательную сторону. Очевидно, что максимальный сдвиг (максимальная расстройка), при котором в системе существуют N стационарных режимов, соответствует максимумам и минимумам периодической функции (2).

Чтобы определить множитель при 8 и убедиться в основательности подстановки расстройки в таком виде, обратимся к одной из форм уравнения движения суммарного вектора из [2]:

d(s = 1 v (с а \d(p

Формула для возвращающей силы (2), по которой строится фазовый портрет системы с произвольным числом АГ, имеет структуру, позволяющую перейти в правой части к безразмерному аргументу x = Л / juS, причем в левой части появляется

безразмерное время т = jit. После такого перехода формула принимает вид

Введем, согласно исходным уравнениям (1), парциальные расстройки в слагаемые -,

составляющие угловую скорость суммарного вектора. Выпишем отдельно члены, содержащие 8 :

jr Z ( S a n) 8.

После вынесения за скобки общего множителя - модуля S - внутри скобок остается сумма проекций на него всех парциальных векторов. Это суммирование, по определению, имеет результатом опять-таки величину S . В итоге множитель при расстройке обращается в единицу, что интуитивно и предполагалось. С введением безразмерного времени величина 8 заменяется отношением 8 / J и уравнение (3) приобретает вид

d(Ps =8/ xy sin($n -(s ) - Tn cos(n -(s ) (4)

Сравним вид полученного уравнения для угловой скорости суммарного вектора (4) с видом исходных уравнений для угловых скоростей парциальных векторов (1).

Парциальный вектор стремится к ориентации в направлении суммы juS + Лк. Наличие расстройки 8 приводит к угловой поправке, пропорциональной отношению 8 к возвращающей силе jS + Ak \.

Суммарный вектор стремится к ориентации в одном из промежуточных направлений, лежащих между направлениями индивидуальных векторов воздействий кк.

Наличие расстройки приводит к угловой поправке, пропорциональной отношению расстройки к возвращающей силе

T2 +1

Отметим, что в последнем случае возвращающая сила, обусловленная ангармонизмом функции F(x), оказывается значительно меньше, чем в первом случае, где

возвращающая сила линейно связана с аргументами в каждом парциальном уравнении. Этой разницей в величинах возвращающих сил объясняется сделанный ранее вывод о том, что расстройка приводит главным образом к повороту всей векторной конфигурации, в то время как отклонение парциальных векторов от векторных сумм jUs + хк остается малозаметным [1].

Примечательно, что анализ динамического режима позволяет уточнить представление о стационарных режимах. Дополнительно к представлению о жесткости

конфигурации в режимах без расстроек появляется основание для того, чтобы распространить понятие жесткости и на режимы с расстройками. В отношении динамики имеется в виду преобладание внутренних сил над внешними и, как результат, сравнительно быстрая перестройка парциальных векторов на фоне медленного поворота конфигурации в целом. В отношении статики имется в виду практическая неизменность конфигурации при всех допустимых расстройках, единственным результатом которых является поворот конфигурации как целого. В связи с этим мы приходим к заключению об универсальности понятия жесткости применительно к векторной конфигурации в исследуемой системе. Два аспекта в поведении системы - статический и динамический - оказываются неразрывно связаны, поскольку стационарный режим с расстройкой эквивалентен переходному процессу с непрерывным равномерным изменением фазы сигнала. Суммарный вектор следует за сигнальным вектором с некоторым отставанием, и когда величина отставания достигает границы сектора устойчивости, процесс становится нестационарным.

Особо примечателен тот факт, что фазовый портрет системы с произвольным числом АГ, построенный в результате анализа ее динамического режима, позволяет определять стационарные положения суммарного вектора в диапазоне допустимых расстроек, а также определять максимально допустимые расстройки без длительных процедур интегрирования системы (1). Впервые значения максимально допустимых расстроек были получены в [1] путем прямого интегрирования системы (1) с подбором величин 8 , соответствующих границе существования устойчивого решения. Результаты представлены на графике рис. 1. Для наглядности в качестве аргумента на графике выбрано отношение амплитуды внешнего сигнала Л к ее предельной величине jlN/2, а в

качестве функции - корень N-й степени из максимальной расстройки, нормированной относительно масштабного коэффициента j . В таком представлении получаются

зависимости, достаточно близкие к пропорциональным, что и позволяет сделать вывод о степенной зависимости полосы синхронизации от амплитуды сигнала. Отметим, что для случая N = 2 имеет место точная пропорция.

0,4 0,6

2Л/ц N

Рис. 1

Благодаря результатам анализа динамического режима аналогичные результаты получаются значительно проще. Согласно (4), предельная расстройка равна максимуму функции F(x), определить который не составляет труда. Остается установить связь

между аргументом x = k/jlS формулы (4) и аргументом 2 Л / jjN. Для этого

воспользуемся результатами расчета стационарных режимов [1], где получена формула, связывающая величины S и Л:

juS + Лcosвk

s = 1

Приводим ее к аргументу X:

S = 1

1 + x cos в.

yjl + x2 + 2x cos вк

S(x,N),

после чего искомая связь между аргументами приобретает вид

2Л/ juN = 2 xS (x, N)/N.

Обозначим максимум функции F(x) величиной M(x,N) . Варьируя параметр x, получаем

заданную в параметрической форме зависимость максимальной относительной расстройки M(x,N) от амплитуды внешнего сигнала 2xS(x,N)/N . На рис. 2 приведены

графики таких зависимостей для различных N.

Электронный научный журнал ИССЛЕДОВАНО В РОССИИ 1 3 2 http: zhurnal.ape.relarn.ru/articles/2006/013.pdf 0,6

0,4 1 0,3

0,2 0,1

0,0 0,2 0,4 0,6 0,8 1,0

2X/jN

Рис. 2

Сравнение с графиками рис. 1 показывает, что, хотя существует приблизительно 10-процентное различие в коэффициенте пропорциональности, однако вывод о степенном характере остается несомненным. Различие объясняется допущением, сделанным при получении формулы (2), а именно пренебрежением малыми угловыми поправками в положении парциальных векторов.

Таким образом, упрощенная динамическая модель [2] позволяет делать правильные качественные выводы о поведении системы, однако, в таком принципиальном вопросе, как расчет помехоустойчивости, количественная неточность ставит применимость данной модели под сомнение. В связи с этим для расчета помехоустойчивости фазового демодулятора на основе исследуемой системы за основу следует принимать исходную систему уравнений (1).

3. Динамика системы двух АГ при малых флуктуациях

Ранее было отмечено, что практическое значение имеют системы с небольшим числом АГ - от 2 до 4. В связи с этим далее основное внимание будет уделено системе двух АГ, для которой многие соотношения получаются в явном виде. Основные свойства такой системы могут быть обобщены на более сложные системы.

В случае двух одинаково настроенных АГ, синхронизуемых сигналом с произвольной расстройкой, аналитическое решение для стационарного режима получается при использовании замены переменных:

а=<Р1 +<Р2 в=(1 -(2 2 2

Угол а в данном случае представляет собой не что иное, как (pS, а угол в - отклонение

парциального вектора a от направления суммарного вектора S. В стационарном режиме без расстройки имеют место соотношения:

sin в = -, cos а = 1. 2ц

Почленным суммированием уравнений для фаз (1 и (?2 получаем

d((\+ (2) = -sm(#1 -(1) + sm(#2 -(2)], dt

причем в данном случае 0Х = П / 2, 62 = - П / 2 ; члены, содержащие параметр взаимной

связи ju, взаимно вычитаются.

Рассмотрим реакцию системы на внешний сигнал со слабо флуктуирующей фазой. Считая, что система находится в окрестности стационарного режима, введем малые отклонения переменных:

в1 =п/2 + ; в2 =-п/2 + ; (1 = arcsin- /2ц) + А(1; (2 = - arcsin- /2ц) + А(2; Ad + А(2 = 2A(s .

Разлагая тригонометрические функции и сохраняя члены первого порядка малости, приходим к уравнению

d (A(S) X 2 ... . . dt 2fi

Согласно этому уравнению, суммарный вектор стремится следовать за отклонением , проявляя при этом инерционность, которая характеризуется скоростью релаксации ЛЛ / 2ц . В операторной форме уравнение имеет вид, типичный для инерционного звена:

Ф s (р) =

1 + Р

Таким образом, система обладает фильтрующими свойствами по отношению к фазовым флуктуациям внешнего сигнала. Чем меньше амплитуда Л, тем в большей степени флуктуации оказываются подавленными. Рассматривая это обстоятельство с точки зрения применения схемы в качестве восстановителя подавленной несущей, приходим к выводу, что уменьшение амплитуды внешнего сигнала является полезным.

Уменьшение амплитуды сигнала имеет смысл до тех пор, пока частота появления ошибок, обусловленных нестабильностью фазы восстановленной несущей, не станет малой в сравнении с частотой битовых ошибок, непосредственно обусловленных аддитивным шумом. Ограничение снизу обусловлено также техническими факторами, прежде всего, неидеальностью настройки автогенераторов. Результат, достигаемый уменьшением амплитуды внешнего сигнала, можно выразить через соотношение полос синхронизации. Отношение полосы синхронизации системы внешним сигналом к полосе

пропускания тракта сигнала А/ примерно определяет, во сколько раз дисперсия фазы

восстановленной несущей меньше дисперсии фазы сигнала. Если удается техническими приемами достичь стабильной работы системы при достаточно малой полосе синхронизации (например, путем применения автоподстройки частоты), то фазовый демодулятор на ее основе приближается по помехоустойчивости к идеальному когерентному демодулятору.

4. Система двух АГ под действием сильных флуктуации

Модуляция фазы сигнала информационным сообщением в сумме с шумом, приближающимся по уровню к сигналу, выводит систему за пределы применимости линеаризованных уравнений с малыми приращениями. Оценить поведение системы при этих условиях позволяет непосредственное интегрирование укороченных уравнений с зависящей от времени правой частью. Соответствующая математическая модель реализована на языке PASCAL. Ее основные компоненты: модель узкополосного шума в виде двух квадратурных составляющих, модель сигнала, модель системы, средства представления результатов. Дискрет по времени выбирается от 1/10 до 1/20 тактового интервала, что позволяет достаточно точно воспроизводить переходные процессы.

Численная модель каждой из квадратурных составляющих узкополосного шума

формируется путем свертки последовательности случайных чисел с выборкой значений

переходной характеристики полосового фильтра, которая представляет собой

модификацию идеализированной характеристики типа sin x / x. Модификация по

принципу весового окна имела целью ограничение длительности выборки при сохранении

приблизительно прямоугольной формы частотной характеристики. Выбранный вариант

переходной функции фильтра имеет вид

(/7Ч sin[;r(t - T/2)/Т] . . . /АГТ1. . АГТ1

h(k) = ------ (0.2 + sm(7rt/4T); t = 0 + 4Т.

n(t - T/2)/T

Сформированная случайная величина нормируется так, чтобы ее дисперсия <J была равна единице. В формировании каждого отсчета участвуют с различными весами 100 случайных величин, так что результат свертки можно считать практически нормально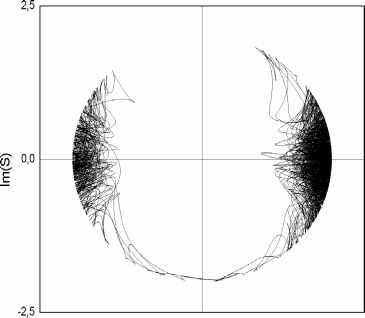

-2,5 0,0 2,5

Re(S) Рис. 3

При имитации процесса демодуляции сигнала представляло интерес выявление различий в частоте появления ошибок у исследуемой схемы и у идеального демодулятора

распределенным. Пик-фактор, вычисленный как сумма модулей отсчетов h(t), составляет около 97, фактически же выбросы не превышают ± 4,5(7 за обозримое время наблюдения.

Действующий на систему фазоманипулированный сигнал имитируется изменением знака относительной амплитуды Л через каждый период тактовой частоты.

В ходе интегрирования уравнений (1) с подстановкой в правую часть шума и сигнала, смоделированных вышеуказанным образом, прослеживалась динамика векторной суммы колебаний парциальных АГ, то есть вектора восстановленной несущей, и вычислялся продукт фазовой демодуляции в виде скалярного произведения векторов сигнала и несущей. Для подсчета числа ошибок производилось посимвольное сравнение исходного и демодулированного сигналов. Ход расчетов визуализировался посредством виртуальной осциллограммы или векторной диаграммы.

В качестве примера на рис. 3 показана траектория конца суммарного вектора в системе двух АГ, синхронизуемой парафазным сигналом. Из рисунка видно, что, имея стационарные позиции 0 и П, фаза суммарного вектора колеблется под действием флуктуаций, эпизодически совершая переходы между указанными позициями. Для данной реализации отношение сигнал/шум составляет 3 дБ, вероятность проскальзывания менее 10-2.