вую. Текущее положение объекта обычно задается через повороты и смещения относительно исходного положения, в котором модельная система координат совпадала с мировой. Следовательно, мировые координаты точек объекта можно получить трансляцией и поворотом соответствующих точек из их исходного положения, в котором их модельные координаты совпадали с мировыми. Большинство графических библиотек выполняют эти преобразования самостоятельно, а программисту остается задать только смещение и поворот для интересующего его объекта. Однако проектировщику все равно нужно знать законы преобразований, чтобы рисовать объекты в нужных местах без проб и ошибок, в особенности если эти объекты перемещаются достаточно сложным образом. В этом разделе мы рассмотрим матрицы преобразования, действуюидие на точки объекта при его перемещении и повороте.

Получив мировые координаты всех точек объекта в его текущем положении, мы должны вычислить координаты этих точек в наблюдательской системе. Перевод координат из одной системы в другую называется отображением (mapping). Отображение между мировой и наблюдательской системами координат обычно также осуществляется графической библиотекой самостоятельно, по заданным программистом координатам точки зрения, точки наблюдения и направлению вектора вертикали (в мировых координатах). Матрица преобразования для операции отображения рассматривается в разделе 3.7.3.

3.7.1. Трансляция

При трансляции объекта на величины а,Ьисв направлениях x,yuz соответственно по отношению в начальному положению, в котором модельная система координат совпадала с мировой (рис. 3.16), мировые координаты точек объекта в новом положении (Xw, Y Z0) вычисляются следующим образом:

Yw=Ym+b; (3.3)

Zw=Zn + с

В этой формуле числа Хт, Ym, Zm являются также модельными координатами точки.

Формула (3.2) может быть записана в матричной форме':

U (3.4)

Trans(a, b, c)

Координаты могут быть также представлены в виде строки. Тогда матрица преобразования записывается после вектора координат. В этом случае матрица преобразования представляет собой транспонированную матрицу из формулы (3.4). В формуле (3.4) мы следуем соглашениям о записи OpenGL.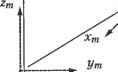

Рис. 3.16. Трансляция объекта

Легко убедиться, что формулы (3.4) и (3.3) эквивалентны друг другу: для этого достаточно записать (3.4) в развернутом виде. Операцию сложения в (3.3) удалось записать через умножение в (3.4) благодаря использованию однородных координат, в которых трехмерный вектор записывается через четыре скаляра вместо трех1. Матрица, которую мы получили, называется матрицей однородного преобразования (homogeneous transformation matrix). В данном случае преобразование является трансляцией. Если бы преобразование (в частности, трансляцию) нужно было применить к точке в двумерном пространстве, однородная матрица преобразования редуцировалась бы до матрицы размерностью 3x3 удалением третьей строки и третьего столбца из матрицы размерностью 4x4. Новая матрица действовала бы на вектор координат размерностью 3x1, полученный из вектора 4x1 удалением г-координаты.

3.7.2. Вращение

Пусть объект поворачивается на угол G вокруг оси х мировой системы координат вместе со своей модельной системой, которая, как и в предыдущем случае, изначально совпадает с мировой (рис. 3.17). Мировые координаты точки объекта в новом положении (Xw, Yw, Z ) могут быть получены из исходных мировых координат этой точки (Хт, Ym, Zm), совпадающих с ее текущими координатами в модельной системе.

Соотношение между (Хи, Y ZJ и (Хт, Ym, Zm) становится очевидным после проецирования рис. 3.17 на плоскость yz. Результат проецирования показан на рис. 3.18.

1 Любой вектор (х, у, z)T трехмерного пространства может быть записан в соответствующих однородных координатах в виде (xw, yw, zw, w)T, где верхний индекс Т обозначает операцию транспонирования. Поскольку значение w может быть произвольным, для каждого вектора существует множество вариантов записи в однородных координатах. В формуле (3.4) используется значение w = 1.

Q(0, YW,ZW)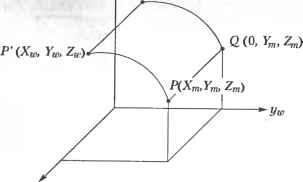

Рис. 3.17. Вращение вокруг оси х Q (Yw> Zw)

Q(Yn,Zm)

Уи>

Рис. 3.18. Проекция на плоскость yz рис. 3.18 можно легко получить следующие равенства:

Yu, = /cos(6 + a) =

= /(cos6cosa-sin6sina) = = /cosacos6-/sinasin6 = = Ym cos 6 -Zm sin 6;

ZK = /sin(6 + a) =

= /(sin0 cos a + cos 6sina) = = / cos asinG + /sina cos 6 = = Ym sin6 + ZOT cos6.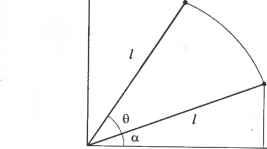

(3.5) (3.6)

(3.7)

Равенства (3.5), (3.6) и (3.7) могут быть записаны в матричной форме:

(3.8)

Матрица в правой части формулы (3.8) - это однородная матрица преобразования вращения вокруг оси х, которая кратко обозначается Rot(xfi). Подобно матрице трансляции, для двумерного объекта однородная матрица вращения редуцируется до размера 3x3.

Однородные матрицы вращения вокруг осей у v\ z получаются аналогичным образом и записываются так:

cos6 0 sine О 0 10 0

-sine о cose о

0 0 0 1

Rot(y,Q) =

(3.9)

Rat(z,Q) =

cos6 -sine 0 0

sine cose oo

0 0 10

0 0 0 1

(3.10)

Мы получили матрицы преобразования, описывающие поворот вокруг мировых осей координат. Можно показать, что поворот вокруг любой произвольной оси раскладывается на повороты вокруг осей х, у и z. Таким образом, матрица преобразования для произвольной оси получается перемножением матриц (3.8)-(3.10).

Как уже отмечалось, матрицы преобразования, описываемые в этом разделе, обычно вычисляются соответствующими подпрограммами графических библиотек. Приведенный ниже код иллюстрирует использование подпрограмм PHIGS и OpenGL.

PHIGS

ptranslate3(Pvector* offset3. Pint* erroMnd. Pmatnx3 result3): /* offset3: вектор трансляции error ind: код ошибки

result3: вычисленная матрица преобразования1 */ protate x(Pfloat angle. Pint* erroMnd. Pmatrix3 result3): protateCPfloat angle. Pint* error ind. Pmatrix3 result3): protate z(Pfloat angle. Pint* erroMnd. Pmatrix3 result3): /* angle: угол поворота

error ind: код шибки

result3: вычисленная матрица преобразования */

OpenGL

glTranslatecKGLdouble offset x. GLdouble offset y. GLdouble offset z). /* Умножает текущую матрицу на матрицу трансляции объекта со смещениями offset x. offsety и offset z по соответствующим осям */

1 В PHIGS матрица преобразования ставится после вектора-строки.

glRotatedCGLdouble angle. GLdouble х. Gldouble у. GLdouble z):

/* Умножает текущую матрицу на матрицу поворота объекта на угол angle против часовой стрелки вокруг луча, проведенного из начала координат в точку (х. у. z). */

Рассмотрим несколько примеров, поясняющих применение матриц преобразований.

Пример 3.1

Объект в трехмерном пространстве транслируется на 5 единиц в направлении у мировой системы координат, после чего поворачивается на 90° вокруг оси х той же системы координат. Если координаты точки объекта в модельной системе имеют значения (0, 0, 1), какими будут мировые координаты этой точки после трансляции и вращения?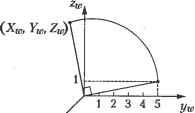

Решение

Координаты (XYZn ) после преобразования трансляции могут быть вычислены следующим образом:

PC У. KY = Trans(0,5,0)[0 0 1 1]т=[0 5 1 1]т. После этого применяется преобразование вращения:

[Хт Yw Zw if = #or(*,90u)[0 5 1 1]т. Следовательно, координаты точки после преобразований будут иметь значения (0,-1, 5). Обратите внимание, что предыдущие выражения можно объединить:

[Xw Ya Z№ If = Rot(x,90°)Trans(0,5,0)[0 0 1 if. Последнее выражение значительно более удобно, особенно при вычислении координат множества точек. В последнем случае матрицы трансляции и вращения перемножаются заранее и дают эквивалентную матрицу преобразования, которая действует на все интересующие нас точки. Процесс вычисления эквивалентной матрицы преобразования путем перемножения отдельных матриц преобразования в соответствующей последовательности называется конкатенацией (concatenation). Возможность выполнения конкатенации - одно из преимуществ использования однородной системы координат, в которой трансляция записывается через матричное умножение, а не через сложение.

Пример 3.2

Объект в пространстве поворачивается на 90° вокруг оси, параллельной оси х мировой системы координат и проходящей через точку с мировыми координа-

тами (0, 3, 2). Если точка объекта имеет модельные координаты (0, 0, 1), какими будут мировые координаты той же точки после поворота?

(0. 0,1)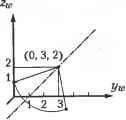

(Хм*, Yj0,2до)

Xw t

Решение

Мы изучили только повороты относительно осей, проходящих через начало ко-, ординат, поэтому нам придется сместить объект вместе с осью вращения. Ось вращения должна проходить через начало координат, причем положение объекта относительно этой оси должно сохраниться. Трансляция объекта вместе с осью на вектор (0, -3, -2) даст нам совпадение оси вращения с осью х мировых координат. Затем мы повернем объект вокруг оси х на 90°, после чего сместим его обратно на вектор (0, 3, 2), чтобы вернуться к исходному положению. Эти операции могут быть записаны следующим образом:

[Хю Yw Zw If =Trans(0,3,2)Rot(x,90°)Trans(0,-3,-2)[0 0 1 if. Обратите внимание на последовательность матриц в этой формуле. Результат легко проверить, применяя преобразования одно за другим, как в примере 3.1.

Раскрывая выражение, получим:

cos 90° sin 90° 0

= [0

о о

1 0 0 0

О

-sin 90° cos 90 0

Результат соответствует приведенной выше иллюстрации. 3.7.3. Отображение

Отображение (mapping) состоит в вычислении координат точки в некоторой системе координат по известным координатам той же точки в другой системе координат. Рассмотрим две системы координат (рис. 3.19). Предположим, что координаты (X2,Y2,Z2) точки Р в системе координат х2 у 2 Ъ должны быть вычислены по координатам (X Yi,Zl )той же точки в системеxyzv Далее, предположим, что вычисление производится применением матрицы преобразования Т^2 к известным координатам:

[Х2 Y2 Z2 If =Tl 2[Xl Yl Z, l]1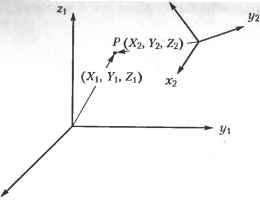

Рис. 3.19. Отображение из одной системы координат в другую

Записав матрицу Тх 2 в явном виде, мы получим из формулы (3.11) следующее выражение:

(3.12)

Чтобы найти неизвестные в уравнении (3.12), подставим в него конкретные значения X, = 0, У, = 0 и Z( = 0, в результате чего получим:

X2=px,Y2=py,Z2=p2. (3.13)

Можно сказать, что рх, ру и р2 определяют координаты начала отсчета системы xlylzl в системе координат x2y2z2.

Теперь подставим в уравнение (3.12) значения Xt = 1, Kt = 0, Zt = 0 и получим:

*2 = пх + рх ,Y2=ny + ру ,Z2=n2+p2. (3.14)

Вычитая формулы (3.13) из (3.14), можно заключить, что пх, пу тлп2 - компоненты х2, у2 и 22 единичного вектора, направленного вдоль оси Х\ системы координат xxyzv Следовательно, коэффициенты пх, пу и п2 легко вычислить с учетом взаимной ориентации систем координат.

Аналогичным образом, о„ оу и о2 представляют собой компоненты х2, у2 и z2 единичного вектора оси уи а компоненты а„ ау и а2 - вектора оси zt. Следующий пример демонстрирует предлагаемую теорию в действии. Пример 3.3

По заданному положению точки зрения (-10, 0, 1), точки наблюдения (0, 0, 1) и вектора вертикали (0, 0, 1) строится наблюдательская система координат (см. представленный ниже рисунок). Обратите внимание, что все координаты и компоненты векторов даны в мировой системе координат. Зная относительное положение системы координат просмотра и мировой системы координат, рассчитать:

□ матрицу преобразования Tw- ;

□ координаты точки с мировыми координатами (5, 0, 1) в наблюдательской системе координат.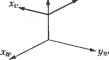

Решение

Первые три числа первого столбца Тк (то есть пх, пу и пг) равны (0 0 -1), поскольку они представляют собой компоненты х„ у и г оси х„,. Аналогично, о„ оу и о2, которые представляют собой компоненты х, у и z оси у,п равны (-10 0), а ау и аг равны (0 1 0). р„ ру и р2 - это координаты х, у„ и zr начала координат системы xwya,zm поэтому они равны 0. -1 и 0 соответственно. В итоге получаем матрицу Tw

-1 О

о о

о о

-1 о 1

Координаты точки (5, 0, 1) в наблюдательской системе мы получим, применив к этому вектору координат только что вычисленную матрицу отображения Та.

Итак, координаты точки (5, 0, 1) в наблюдательской системе имеют значения (0, О, -5), о чем можно догадаться, посмотрев на приведенный рисунок.

Пример 3.4

Точки зрения и наблюдения имеют координаты (5, 5, 5) и (0, 0, 0) соответственно, а вектор вертикали выбирается равным (0, 0. 1). Проекция изометрическая. Необходимо вычислить матрицу преобразования отображения T ,v и наблюдательские координаты точки с мировыми координатами (0, 0, 5).

Решение

Наблюдательская система координат может быть изображена так, как показано на рисунке выше. Заштрихованный треугольник на этом рисунке параллелен плоскости экрана. В этой плоскости лежат оси х„ и у1Г

Чтобы вычислить элементы T№ v, нам нужно получить компоненты х, yv и 2 осей z№. Для этого обозначим единичные векторы осей xv, у„ и z буквами iv jv и kv соответственно. Единичные векторы осей хйп уи, и zw будут называться просто i, j и к. Единичный вектор kv направлен из точки наблюдения в точку зрения, поэтому

1 . 1 . 1 .

= -pi + -p J + л/3 V3

Как отмечалось в разделе 3.2, единичный вектор jv должен быть коллинеарен проекции вектора вертикали на экран. Другими словами, его направление будет совпадать с направлением вектора, полученного вычитанием из вектора вертикали составляющей, перпендикулярной экрану. Обозначив вектор вертикали и , запишем выражение для jv. Р'

1. 1. 2,

-1--J+-K

3 3 3

Jv =

(u kv)kv

1 р -( р -kv)kv

1. - i

1 . 2, j+ k

3 3

= -- i-- + -k л/б л/б 1 л/6

Последний единичный вектор iv вычисляется через векторное произведение:

1 1

Теперь вычислим nx - компоненту х„ оси х№,

. . 1

Аналогичным образом, компонента пч равна

как произведение:

а компонента п2 равна

Таким же путем получим второй и третий столбцы матрицы T , v. Компоненты Рх, ру ир2 можно не вычислять, потому что в этом примере начала координат наблюдательской и мировой систем совпадают. Следовательно, матрица преобразования выглядит так:

Г =

tP-V

Координаты точки (0, 0, 5) в наблюдательской системе имеют значение

\XV У„ Zv 1]Т=Г [0 0 5 1]т =

0 5л/б 5л/б 1

Экранные координаты точки в изометрической проекции получаются из наблюдательских координат непосредственно:

о 5f.

Изометрическая проекция относится к параллельным, поэтому все точки на оси zw проецируются на ось у экранных координат. Фактически задание вектора вертикали, равного (0, 0, 1), означает, что после проецирования ось zw представляется на экране в виде вертикальной прямой.

3.7.4. Другие матрицы преобразования

Помимо матриц преобразования, рассмотренных в предыдущих разделах, часто используются матрицы масштабирования и зеркального отображения. Для масштабирования объекта с коэффициентом sx по оси х, sy по оси у, s2 по оси z применяется следующая матрица преобразования:

(3.15)

Для двумерных объектов матрица масштабирования редуцируется до размера 3x3, как это было с матрицами трансляции и поворота. Эффекта масштабирования можно достичь, изменив размеры видового экрана или окна, не меняя значений координат.

Матрица преобразования (3.15) используется при масштабировании объекта относительно начала координат. Часто бывает необходимо масштабировать объект относительно одной из его точек Р с координатами (Хр, Yp, Zp). В этом случае сначала к точке Р применяется преобразование трансляции Trans(-Xp, - Yp, -Zp), которое перемещает эту точку в начало координат, затем применяется матрица масштабирования из (3.15), после чего объект возвращается в исходное положение действием Trans(Xp, Yp, Zp).

Отражение относительно зеркальной плоскости ху может быть достигнуто при помощи приведенной ниже матрицы преобразования. Преобразование заключается в изменении знака координаты г.

(3.16)

Матрицы преобразования для других отражений (относительно плоскостей xz и yz) выводятся аналогичным образом.

3.8. Удаление невидимых линий и поверхностей

Проекция на экран станет более наглядной, если будет содержать только видимые линии и поверхности. Удаление невидимых линий (hidden-line removal) заключается в блокировании отображения отрезков, скрытых от наблюдателя, а удаление невидимых поверхностей (hidden-surface removal) есть то же самое по отношению к поверхностям. Удаление невидимых линий иллюстрируют рис. 3.20 и рис. 3.21. Очевидно, что эта процедура значительно облегчает восприятие объекта.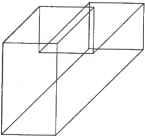

Рис. 3.20. Изображение до удаления невидимых линий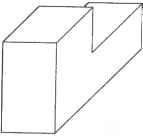

Рис. 3.21. Изображение после удаления невидимых линий

Опубликовано множество программных алгоритмов удаления невидимых линий и поверхностей. Их авторы пытаются повысить вычислительную эффективность и расширить диапазон объектов для применения своих алгоритмов. Однако лучше всего удаление реализуется посредством графического устройства, которое называется г-буфером1, поэтому в настоящее время исследования на эту тему практически не ведутся. В настоящем разделе мы рассмотрим несколько типичных алгоритмов удаления скрытых линий и поверхностей программным путем, а также изучим метод использования для той же цели z-буфера.

1 Z-буфером называется область памяти, аналогичная буферу кадра в том смысле, что в ней хранятся данные обо всех пикселах. Однако в г-буфере хранятся не цвета пикселов, а z-коордннаты объектов, к проекциям которых эти пикселы относятся. Координата г измеряется в наблюдательской системе и потому является мерой расстояния от наблюдателя до объекта.

3.8.1. Алгоритм удаления невидимых граней

Алгоритм удаления невидимых граней (back-face removal algorithm) основан на том, что грань объекта может быть видимой только в том случае, если вектор внешней нормали к этой грани направлен в сторону наблюдателя. В противном случае грань будет невидима. Например, верхняя грань бруска, изображенного на рис. 3.22, считается видимой, если вектор внешней нормали N имеет положительную составляющую в направлении вектора М, проведенного из точки на грани к наблюдателю. Математически это записывается так:

□ если М N > 0, поверхность видима;

□ если М N = 0, поверхность проецируется в отрезок;

□ если М N < 0, поверхность невидима.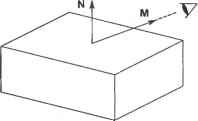

Рис. 3.22. Векторы, определяющие видимость грани

Этот алгоритм легко применить к объекту, ограниченному плоскими поверхностями, поскольку вектор нормали N постоянен в пределах поверхности. Однако к вогнутому1 объекту алгоритм неприменим, поскольку грань, направленная к наблюдателю, может быть закрыта другой гранью того же объекта (рис. 3.23). Та же проблема возникает в случае нескольких выпуклых объектов, которые могут закрывать грани друг друга. Следовательно, алгоритм удаления невидимых граней применим только к одному выпуклому объекту. Более того, алгоритм неприменим к объектам, для которых вектор внешней нормали определяется неоднозначно2 (см., например, рис. 3.24).

Если поверхности объекта не являются плоскими, значение N будет меняться в пределах одной грани в зависимости от выбранной точки. Одновременно может меняться и знак произведения М N. Это означает, что у одной и той же грани будут как видимые, так и невидимые участки. Поэтому грань должна быть разделена на две части вдоль кривой, на которой выполняется равенство М N = 0. Эта кривая называется силуэтной линией (silhouette line). После разделения грани вдоль силуэтной линии знак М N будет постоянным на каждой из частей грани. Процедура может показаться легкой, но рассчитать силуэтную линию очень сложно, а из-за этого теряется главное преимущество алгоритма удаления невидимых граней - простота реализации.

1 Объект называется вогнутым, если по крайней мере две его грани смыкаются под внутренним углом, большим 180°. Если все грани смыкаются с внутренними углами, меньшими 180°, объект называется выпуклым.

2 Такой объект вообще представляет собой достаточно сложную проблему, о чем будет рассказано в главе 5.

Рис. 3.23. Пример вогнутого объекта

После того как все грани классифицируются как видимые или невидимые, на экран выводятся ребра видимых граней, в результате чего получается рисунок без невидимых линий. Если же нужно получить рисунок без невидимых поверхностей, видимые поверхности заливаются выбранными цветами.

Рис. 3.24. Объект с неоднозначно определенным вектором внешней нормали

3.8.2. Алгоритм художника

Основной принцип алгоритма сортировки по глубине, или алгоритма художника (depth-sorting, painters algorithm), можно представить следующим образом. Поверхности объектов сортируются по удаленности от наблюдателя и заполняются соответствующими цветами, начиная с самой дальней. В результате закрашивания поверхностей в данной последовательности дальние поверхности автоматически скрываются ближними, если они проецируются в одну и ту же область экрана. Таким образом, алгоритм художника работает как алгоритм удаления невидимых поверхностей.

Расстояние от поверхности до наблюдателя определяется г-координатами точек на этой поверхности в наблюдательской системе координат. Точка с большей координатой Zv считается находящейся ближе к наблюдателю1. Здесь и далее z-ko-ордината в наблюдательской системе координат будет обозначаться Z . Значит, остается только сравнить координаты Z всех поверхностей и отобразить их, начиная с поверхности с наименьшим значением Zt,.

1 В OpenGL точки с большими Z находятся дальше от наблюдателя, поскольку эта библиотека основана на левосторонней наблюдательской системе координат.

Легко сравнивать координаты Z поверхностей, если максимальное значение Zr одной из них меньше минимального значения Z другой. Однако в большинстве случаев диапазон значений Z точек одной поверхности перекрывается с диапазоном Z другой поверхности. Неоднозначности можно избежать, разбивая все поверхности на отдельные части до тех пор, пока диапазоны Zr не перестанут перекрываться. Есть и другой, более простой п реализации способ решения проблемы. Все поверхности преобразуются в наборы небольших треугольников таким образом, чтобы диапазоны Zp разных треугольников не перекрывались друг с другом, после чего треугольники окрашиваются в соответствующие цвета в нужной последовательности. Чем меньше размер треугольников, тем меньше шансов, что их диапазоны Zv перекроются. Такое приближение поверхности объекта называется триангуляцией (triangulatiori) или фасетированием.

3.8.3. Алгоритм удаления невидимых линий

Алгоритм сортировки по глубине используется для удаления невидимых поверхностей. Алгоритм невидимых граней позволяет построить рисунок со скрытыми линиями, но имеет множество ограничений в общем случае. При применении алгоритма невидимых граней к множеству объектов удалено будет лишь около 50% невидимых линий. Нам нужен алгоритм, который удалял бы все невидимые линии независимо от количества объектов, их выпуклости и наличия криволинейных поверхностей.

Один из таких алгоритмов действует следующим образом. Для каждого ребра1 каждого объекта производится проверка, не закрыто ли оно гранями2 каких-либо объектов. Закрытые части ребер последовательно исключаются до тех пор, пока не останется непроверенных поверхностей. Оставшиеся части всех ребер выводятся на экран.

Реализация алгоритма включает несколько этапов.

1. Поверхности, направленные к наблюдателю, выделяются из всех остальных в отдельную группу при помощи алгоритма невидимых граней. Выделенные поверхности сохраняются в массив FACE-TABLE. Грани, направленные от наблюдателя, учитывать не требуется, поскольку они сами по себе скрыты, а потому не скрывают ребра других граней. Для каждой грани сохраняется максимальное и минимальное значение Zt.. Криволинейные поверхности разделяются по силуэтным линиям (как в алгоритме невидимых граней), а видимые части этих поверхностей также сохраняются в массиве FACE-TABLE вместе с плоскими гранями.

2. Ребра граней из массива FACE-TABLE выделяются из всех прочих ребер и собираются в отдельный список. Ребра других граней, не входящих в FACE-TABLE, можно не рассматривать, поскольку они невидимы. Затем для каждого ребра из списка производится проверка, не закрывается ли это ребро гранью из FACE-TABLE.

1 Ребром объекта называется кривая пересечения соседних поверхностей, ограничиваю щих внутренний объем объекта.

2 Гранями называются поверхности, ограничивающие объем объекта. Площадь любой гра ни конечна, потому что все грани ограничиваются ребрами.

3. Скрытие ребра гранью можно обнаружить, сравнивая диапазоны значений Z ребра и грани. Возможны три случая (рис. 3.25). В случае рис. 3.25, а все значения Z ребра меньше минимального значения Z грани, то есть грань находится перед ребром. В случае рис. 3.25, б значения Z ребра больше максимального значения Z грани, то есть грань находится за ребром. В случае рис. 3.25, в диапазоны значений Z грани и ребра перекрываются, то есть часть ребра находится за гранью, а другая часть - перед ней. Если ребро находится перед проверяемой гранью, из массива FACE-TABLE выбирается следующая грань и ребро сравнивается уже с ней. Если ребро оказывается за гранью, или проходит ее насквозь, приходится выполнять дополнительное действие.

4. Ребро и грань проецируются на экран, после чего производится проверка перекрытия проекций. Если перекрытия нет, из этого следует, что ребро не закрывает проверяемую грань. Из массива FACE-TABLE выбирается следующая грань и проверяется согласно пункту 3. Если проекции перекрываются, ребро делится на две части в той точке, где она проходит сквозь проверяемую грань (рис. 3.26). Закрытая часть ребра отбрасывается, а видимые части добавляются в список. Затем пункт 3 повторяется для новых элементов списка. Исходное ребро из списка удаляется.

5. Ребра, прошедшие проверку со всеми гранями из FACE-TABLE, считаются видимыми и выводятся на экран.

Перед гранью

а б

Рис. 3.25. Три возможных положения грани и ребра

Рис. 3.26. Разбиение ребра

3.8.4. Метод z-буфера

Метод z-буфера основан на том же принципе, что и алгоритм сортировки по глубине: на любом участке экрана оказывается проекция элемента, расположенного ближе всех прочих к наблюдателю. Здесь под элементами понимаются точки, кривые или поверхности. Данный метод требует использования области памяти, называемрй z-буфером. В этом буфере для каждого пиксела хранится значение координаты Zp того элемента, проекция которого изображается данным пикселом. Как уже говорилось, значение Z (то есть координата z в наблюдательской системе) есть мера удаленности объекта от наблюдателя. Объем z-буфера опре-

деляется количеством пикселов, для каждого из которых требуется сохранить вещественное число.

Грани, векторы нормали которых направлены от наблюдателя, невидимы для него, поэтому на экран проецируются только те грани, векторы нормали которых направлены к наблюдателю. Однако в отличие от метода сортировки по глубине, в данном случае порядок проецирования значения не имеет. Причина станет очевидной, как только вы прочитаете приведенное ниже описание алгоритма. Сначала проецируется произвольно выбранная поверхность, и в ячейки памяти z-буфера, соответствующие пикселам проекции поверхности, записываются значения координат Z точек поверхности, являющихся прообразами данных пикселов. Пикселы окрашиваются в цвет первой поверхности. Затем проецируется следующая поверхность, и все неокрашенные пикселы, относящиеся к ее проекции, окрашиваются в цвет второй поверхности. Если пикселы уже были окрашены, соответствующие им значения Z,. сравниваются со значениями Z точек текущей поверхности. Если сохраненное значение Z какого-то пиксела оказывается больше текущего (то есть точка на предыдущей поверхности ближе к наблюдателю, чем точка на текущей поверхности), цвет пиксела не меняется. В противном случае пиксел окрашивается в цвет текущей поверхности. Изначально z-буфер инициализируется координатами Z, соответствующими дальней плоскости (см. рис. 3.11), поэтому пикселы проекции первой поверхности автоматически окрашиваются в ее цвет. Повторяя эту процедуру для всех имеющихся плоскостей, мы окрасим все пикселы экрана в цвета ближайших поверхностей (рис. 3.27).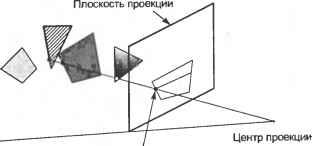

Пиксел имеет тот же цвет, что и ближайшая поверхность

Рис. 3.27. Основы метода z-буфера

Как следует из предшествующего описания, метод z-буфера предназначен главным образом для удаления скрытых поверхностей, как и метод сортировки по глубине. Однако метод z-буфера с небольшими изменениями позволяет реализовать и построение рисунков со скрытыми линиями. Сначала все поверхности проецируются на экран, причем пикселы окрашиваются в цвет фона (на экране ничего не появляется). При этом z-буфер заполняется правильными значениями Zv. Затем на экран проецируются ребра поверхностей. При этом значения Z ребер сравниваются со значениями Zv ближайших к наблюдателю поверхностей, уже найденными на предыдущем этапе. Окрашиваются только те пикселы, для которых новые значения Z, больше исходных. Таким образом, участки ребер,

скрытые поверхностями, на экране не появляются. Эта процедура дает правильный рисунок без скрытых линий, но некоторые граничные линии могут оказаться слишком тонкими, потому что некоторые пикселы этих линий будут относиться к поверхностям, ограниченным соответствующими ребрами. Эту проблему легко решить, пододвинув весь объект поближе в момент проецирования ребер.

3.9. Визуализация

Изображения без невидимых линий и поверхностей в большинстве случаев передают форму объекта достаточно хорошо. Однако для некоторых приложений желательно иметь возможность строить более реалистичные изображения. Особенно важную роль реалистичность играет в виртуальной реальности - относительно новой технологии, позволяющей имитировать на компьютере реальные ситуации. Например, вы можете занести в компьютер сведения о внутреннем и внешнем виде проектируемого здания, а затем пройтись по нему и вокруг него, чтобы прочувствовать, как оно будет выглядеть на самом деле. Это средство может оказаться очень полезным для принятия решения о вложении денег в постройку здания.

Для имитации реальной сцены нужно воспроизвести эффекты, создаваемые светом, падающим на поверхности объектов. Этот процесс называется визуализацией или тонированием (rendering). Вообще говоря, все, что мы видим, - это отражение света от поверхностей, а по этому отраженному свету мы определяем форму, текстуру и цвет объекта. В усовершенствованных графических библиотеках обычно имеются некоторые средства визуализации. Для их применения достаточно задать фасетированную модель объекта, условия освещенности и свойства поверхностей (например, блестящие или тусклые). Однако для правильного использования технологий визуализации необходимо иметь представление об их основах. Даже задать правильные значения параметров функций визуализации без достаточно хорошего знания техники визуализации непросто. Поэтому в настоящем разделе мы коротко опишем две основные технологии визуализации: затушевывание (shading) и трассировка лучей (ray tracing). Подробное описание технологий визуализации можно найти в большинстве книг по компьютерной графике.

3.9.1. Затушевывание

Процедура затушевывания аналогична удалению невидимых поверхностей с той разницей, что пикселы одной поверхности окрашиваются разными цветами в соответствии с цветом и интенсивностью отраженного света в точке, проектируемой Ra = Kdlu на этот пиксел. Таким образом, основной задачей становится расчет цвета и интенсивности света, отраженного от какой-либо точки объекта. Начнем с расчета интенсивности.

Поверхность объекта может быть освещена светом, исходящим непосредственно от источников, то есть прямым светом (direct illumination), а также светом, отраженным от других поверхностей, дающим окружающее освещение (ambient illumination). Свет, отраженный данной точкой объекта, получается сложением отраженных лучей двух типов (рис. 3.28).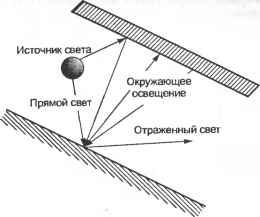

Рис. 3.28. Прямое и окружающее освещение

Отраженный от множества поверхностей сцены свет может считаться приходящим с бесчисленного множества направлений, поэтому отражение окружающего освещения считается равномерно распределенным во всех направлениях. Поэтому интенсивность отражения Ra записывается по формуле:

Rn=KdI . (3.17)

Здесь 1и - интенсивность окружающего освещения, a Kd - коэффициент отражения поверхности. У белых поверхностей коэффициент отражения близок к единице, а у черных - к нулю. Наблюдатель будет воспринимать одну и ту же интенсивность отраженного окружающего освещения вне зависимости от своего положения, поскольку это освещение образуется благодаря отражению от всех поверхностей и распределяется равномерно по всем направлениям.

Для описания прямого освещения достаточно рассмотреть лишь точечные источники света, поскольку линейные и поверхностные источники могут быть рассмотрены как совокупность точечных. Отражение света от точечного источника рассматривается как комбинация двух видов отражения: диффузного и зеркального.

Диффузное отражение (diffuse reflection) состоит в том, что поверхность поглощает свет, а затем переизлучает его равномерно во всех направлениях (рис. 3.29). Интенсивность диффузного отражения (как и отражения окружающего освещения) не зависит от положения наблюдателя. Особенности структуры поверхности, такие как текстура и цвет, становятся видимыми именно благодаря диффузному отражению. Для грубых поверхностей отражение является преимущественно диффузным, а не зеркальным.

Зеркальное отражение (specular reflection) - это прямое отражение света поверхностью. Данный тип отражения характерен для блестящих поверхностей, таких как зеркала. Блестящие поверхности отражают почти весь падающий свет и по-

тому обладают повышенной яркостью (рис. 3.30). Интенсивность зеркального отражения воспринимается по-разному в зависимости от положения наблюдателя относительно сцены.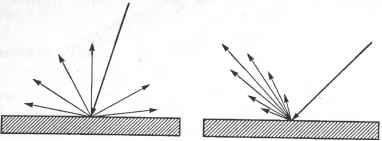

Рис. 3.29. Диффузное отражение Рис. 3.30. Зеркальное отражение Опишем процедуру расчета ннтенсивностей диффузного и зеркального отражения. Когда мы сделаем это, интенсивность отражения света от точечного источника можно будет приближенно описать как сумму отражений указанных двух типов. Интенсивность диффузного отражения прямо пропорциональна косинусу угла падения. Углом падения в данной точке называется угол между вектором нормали к поверхности и вектором, направленным из точки к источнику света (рис. 3.31).

Вектор нормали Падающий свет д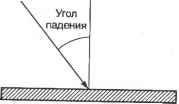

Рис. 3.31. Определение угла падения

Это соотношение называется законом косинусов Ламберта. Его легко проверить, представив падающий пучок в виде конечного числа параллельных линий, нахо-йящихся на одинаковом расстоянии друг от друга (рис. 3.32). Обратите внимание, что количество лучей, падающих на поверхность, уменьшается с ее наклоном, □тсюда следует, что интенсивность отраженного света с наклоном поверхности гакже будет падать.

Рис. 3.32. Иллюстрация к закону Ламберта

Математически закон косинусов Ламберта может быть выражен так. Интенсивность падающего света в интересующей нас точке 1р считается обратно пропорциональной квадрату расстояния до источника света £>;, поэтому для источника интенсивностью Ер она запишется так:

/, (3.18)

Обычно предполагается, что все источники света установлены достаточно далеко от поверхностей, так что D/ может считаться одинаковым для всех точек. Тогда закон Ламберта запишется независимо от D,\

Ra =KdEp(KL). (3.19)

Здесь Rd - интенсивность диффузного отражения, Кл - коэффициент отражения (см. формулу (3.17)), N - единичный вектор нормали к поверхности в интересующей нас точке, L - единичный вектор, направленный от точки к источнику света, а N L - косинус угла падения. Вектор L постоянен для всех точек, поскольку источник считается расположенным достаточно далеко.

Используя формулу (3.19), можно столкнуться со следующей проблемой: две параллельные плоскости, частично перекрывающиеся на экране, будут казаться наблюдателю неразличимыми. Лучше, если бы плоскость, расположенная ближе, казалась более яркой, то есть имела большее значение Rd. Такого эффекта можно достичь, изменив формулу (3.19):

К Е

Rd ~(N-L). (3.20)

D + D0

Здесь D - расстояние между интересующей нас точкой и точкой зрения наблюдателя, а постоянная D0 позволяет избежать деления на нуль.

Теперь займемся расчетом интенсивности зеркального отражения. Было сделано множество попыток точно промоделировать зеркальное отражение. Мы рассмотрим одну типичную модель, которая носит название модели Фонга (Phong model). Большая часть отраженного света попадает в небольшой конический объем вокруг оси, угол которой совпадает с углом падения, но находится по другую сторону от нормали к поверхности (рис. 3.33). Эта ось на рисунке обозначена единичным вектором R. Интенсивность воспринимаемого наблюдателем света будет спадать по мере удаления вектора зрения (единичный вектор V на рис. 3.33) от вектора R. Фонг предложил следующую формулу для описания этого эффекта:

R =7Г7Г^<УК> - <3-21)

D + D0

Здесь Ер, D и D0 имеют тот же смысл, что и в формуле (3.20), a Ks - константа, аналогичная Kd в той же формуле. Ks называется коэффициентом зеркального отражения. Формулу (3.21) можно интерпретировать так: интенсивность света, воспринимаемого наблюдателем, вектор зрения которого отклоняется от оси R на угол ф, пропорциональна (cos ф) . Таким образом, интенсивность отражения быстро спадает с удалением от угла отражения, если п много больше единицы, то есть отраженный свет распространяется плотным пучком вдоль оси R. Поэтому у блестящих поверхностей, например металлических, значение п должно быть большим. Например, для такой поверхности хорошо взять значение п