
|
| |||
|
Разделы
Главная
Сапромат
Моделирование
Взаимодействие
Методы
Инновации
Индукция
Исследования
Факторизация
Частоты
Популярное
Как составляется проект слаботочных сетей?
Как защитить объект?
Слаботочные системы в проекте «Умный дом»
Какой дом надежнее: каркасный или брусовой?
Как правильно создавать слаботочные системы?
Что такое энергоэффективные дома?
|
Главная » Сапромат 1 ... 25 26 27 28 29 Алгоритм де Кастильо Алгоритм де Кастильо можно сформулировать следующим образом. Р(м), координаты точки на кривой Безье при значении параметра, равном и, равны Р0 и вычисляются по следующей рекурсивной формуле: р; =(1-и)р;-! +uv;;l, (е.1) где r= 1.....п; i = 0,п - г; Р° =Р а начальные значения Р° - это координаты задающих точек Р,. Выражение (е.1) показывает, что Р/ вычисляются по Р°, или что задающие точки Р2 вычисляются по Р/ и т. д., пока не будет получено - значение Р(м). Этот процесс показан на рис. е.1 для кривой Безье порядка 3 (я = 3). Обратите внимание, что P,J получается путем разбиения сегмента линии Р„Р, на отрезки с отношением длин и : (1 - и), Р,! и Р2 определяются так же. Затем находится Р%, для чего сегмент линии Р^Р/ разбивается на отрезки с тем же отношением длин, а после этого определяются Рр или РЦ путем аналогичного разбиения сегмента PqPi2- Pq дает координаты точки кривой, соответствующей значению параметра и. Как вы помните, значение параметра определяет отношение, в котором разбиваются соответствующие сегменты линии. Рисунок е.1 показывает также, что исходная кривая Безье состоит из двух кривых Безье: одна определена четырьмя задающими точками Р0, Pq , Р02 и Pq , а другая - Рд, Р,2, Р2 и Р3. Проверку этого утверждения можно найти в [48]. Обратите также внимание, что два новых задающих многоугольника аппроксимируют оригинальную кривую Безье гораздо более близко, чем исходный задающий многоугольник. Таким образом, алгоритм де Кастильо может применяться многократно для аппроксимации кривой Безье сегментами прямых линий. Процесс получения РЦ с помощью формулы (е.1) иллюстрируется схематически на рис. е.2. Любая точка Р,г определяется верхним левым соседом Р{г 1 и левым соседом Р,г+~, следовательно, новые точки, создаваемые в процессе рекурсии, образуют нижний треугольник с вершиной в Р0 . Эта схематическая диаграмма содержит дополнительную полезную информацию. Мы показали, что кривая Безье порядка 3 в процессе применения алгоритма де Кастильо может быть разделена на две кривые Безье того же порядка. Эту идею можно распространить на кривую Безье любого порядка. На самом деле две группы точек, окруженные пунктирными линиями, - это задающие точки двух кривых Безье, полученных путем разделения исходной кривой Безье, определенной точками Р0, Р .... Р„. Таким образом, кривую Безье любого порядка можно разбить на множество кривых Безье того же порядка, многократно применяя алгоритм де Кастильо, и результирующие задающие многоугольники будут достаточно близко аппроксимировать исходную кривую. Такая аппроксимация прямолинейными сегментами может использоваться для вычисления начальных значений точек пересечения между кривыми Безье. Реализация алгоритма де Кастильо на языке с представлена в листинге е.1. с помощью алгоритма де Кастильо можно также вычислить производные кривой Безье. Дело в том, что производная любого порядка от кривой Безье может быть выражена уравнением кривой Безье, как отмечалось в разделе 6.4.1. 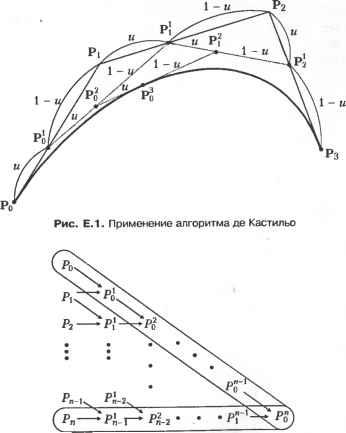 Рис. Е.2. Схематическая иллюстрация алгоритма де Кастильо Листинг Е.1. Реализация алгоритма де Кастильо на языке С float decas(degree, coeff. и) /* Использует алгоритм де Кастильо для вычисления одной координаты точки кривой Безье. Должна вызываться для каждой координаты (х. у и/или z) задающего многоугольника. degree: степень кривой Безье coeff: массив коэффициентов кривой и: значение параметра Выход: значение координаты int degree: float Coeff[]; float U; { int r. i; float ul: float coeffa[30]: /* дополнительный массив измените размерность, если его недостаточно */ ul = 1.0 - и: for(i=0: i<=degree: i++) coeffa[i] = coeff[i]: /* сохраняем входной массив */ for(r=l: r<=degree: r++) for(i-0: i<=degree-r: i++) { coeffa[i] = ul * coeffa[i] + u * coeffa[i+l]: return(coeffa[0]): i=/-*+l ,=/-*+1 ь,+ I = I 7 (=/-*+ 2 С, u-t, U-t; = I i+U- (Ж.1) !=/-*+2 где Р/ определяется следующим образом1: Таким образом, Р? можно интерпретировать как внутреннюю точку разбиения сегмента линии Р;Р, ., аналогично алгоритму де Кастильо. Теперь ЛГуц выражается через комбинацию Л/ 2 и 4+i,*-2 с помощью формулы (6.32), и это выражение подставляется в уравнение (Ж.2) вместо NIJt x. После этого, используя процесс, аналогичный тому, который применялся при выводе уравнения (Ж.2), мы можем получить следующее соотношение: Во второй строке (Ж.2) делается подстановка j = i + 1, а в третьей строке диапазон суммирования сужается, поскольку Л и Л^-цц равны нулю в интервале tx и Вычисление В-сплайновой кривой по методу Кокса-де Бура Опишем вычисление В-сплайновой кривой по методу Кокса-де Бура. Для этого мы вычислим координаты В-сплайновой кривой для параметра и в диапазоне t( < и < tl+l. Когда и находится в этом диапазоне, достаточно рассмотреть только Ыц. Распространяя эффект NtA (см. рис. 6.5), мы можем заключить, что только функции сопряжения Л 1)А, могут иметь ненулевые значения. Поэтому выражение для Р(м) можно изменить следующим образом: P(u) = ±P,Nik(u)= £p,jv,a( )- i-О Ы1-к+1 Подставляя уравнение (6.32) в уравнение (Ж.1), получаем: Приложение Ж. Вычисление В-сплайновой кривой по методу Кокса-де Бура р( )= £р/Ч.*-2. (Ж.4) 1=/-*+3 где Р? определяется следующим образом: p = !iz!l p-+fl £zfl V Иными словами, Р(2 также представляет собой внутреннюю точку разбиения сегмента линии P/P/ i. Повторив ту же процедуру произвольное число раз г, мы получим: р( )= ЕВД.*- , (Ж.5) !=/-*+г+1 где р; = - р;- +1 ! р[:;. (ж.б) Р[ носит название точки де Бура. Обратите внимание, что под Р° в выражении (Ж.б) понимается Р,. Делая в уравнении (Ж.б) подстановку r=(k - 1), получим Р(и) = Р,* Ч ,(и) = Р;- (Ж.7) Поэтому мы можем сказать, что координаты точки, соответствующей значению параметра и в диапазоне t, < и < t,+i, - это координаты Р,* 1, получаемые путем рекурсивного разбиения сегментов линий между соответствующими точками, начиная с сегмента между двумя исходными задающими точками. Пример Ж.1 Для кривой В-сплайна, показанной в примере 6.4, вычислите координаты точки, соответствующей и = 2,5, используя алгоритм Кокса-де Бура. Решение В соответствии с условием примера 6.4 значения узлов таковы: t0 = 0, г, = 0, t2 = 0, Гз = 1, U = 2, ts = 3, te = 4, t, = 4, fe = 4. Таким образом, в данном случае / становится равным 4, поскольку t4 < 2,5 < t5, и в соответствии с уравнением (Ж.7) Р(2,5) = Р2. Используя уравнение (Ж.б), можно выразить Р42 как 1 з - Рз = (Ж.8) к-t. , IА u-t Р\ < = 0,5Р4 +0,5Рз. Обратите внимание, что при выводе уравнения (Ж.8) были подставлены значения k = 3 и и = 2,5. Можно также получить Р\ и Р3, используя уравнение (Ж.б): Вычисление В-сплайновой кривой по методу Кокса-де Бура Р. =ii P4 JI-OZL-V Цр4 +Р3; t6-t* \ h-ti) 4 4 Р-=21Рз+[{ -гз f 5 3 У 3 1 Р, =£р3 + р2. 2 4 3 4 2 (Ж.9) Обратите внимание, что Р° заменяется на Р как и прежде. Теперь можно найти точку Р(2,5) на кривой (см. рис. 6.6), используя уравнения (Ж. 10), (Ж.9) и (Ж.8), как показано на рис. Ж.1. 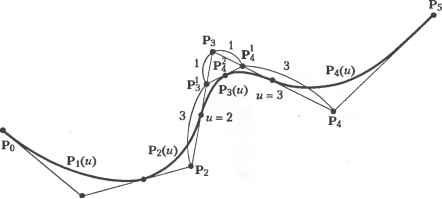 Рис. Ж.1. Создание точки Р[ Рисунок Ж.1 показывает, что исходная кривая В-сплайна разделена на две кривые В-сплайна того же порядка, как это делалось для кривых Безье: одна кривая определена задающими точками Р„, Р Р2, Рз и Р42, а другая - Р2, Р4, Р4 и Р5. Первая кривая В-сплайна имеет пять задающих точек (и = 4) и порядок 3 (k = 3), так что она имела бы узловые значения [0 0 0 1 2 2,5 2,5 2,5]. Аналогичным образом, вторая кривая В-сплайна имела бы узловые значения [2,5 2,5 2,5 3 4 4 4]. Процесс итеративного вычисления Р,* с использованием уравнения (Ж.б) можно иллюстрировать схематически (рис. Ж.2). Любая точка Р[ определяется верхним левым соседом Р[~* и левым соседом Р[~1, следовательно, новые точки, создаваемые в процессе рекурсии, образуют нижний треугольник с вершиной в Р,*-1. Эта схематическая диаграмма содержит дополнительную полезную информацию. Мы показали, что кривая В-сплайна порядка 3 в процессе применения алгоритма Кокса-де Бура в примере Ж.1 может быть разделена на две кривые В-сплайна того же порядка. Эту идею можно распространить на кривую В-сплайна любой степени, как и в случае кривых Безье. На самом деле две группы точек на рис. 6.12, окруженные пунктирными линиями, - это задающие точки двух кривых В-сплайна, полученных путем разделения исходной кривой В-сплайна, определенной точками Р0, Р,.....Р„, в точке, где параметр и принимает значение с, < и < ti+x. Таким образом, кривую В-сплайна любого порядка можно разбить на множество кривых В-сплайна того же проядка, многократно применяя алгоритм Кокса-де Бура, и результирующие задающие многоугольники будут достаточно Приложение Ж. Вычисление В-сплайновой кривой по методу Кокса-де Бура близко аппроксимировать исходную кривую, как и в случае применения алгоритма де Кастильо для аппроксимации кривой Безье. Такая аппроксимация прямолинейными сегментами может использоваться для вычисления начальных значений точек пересечения между кривыми В-сплайна. Алгоритм Кокса- де Бура может быть реализован на языке С (листинг Ж.1). 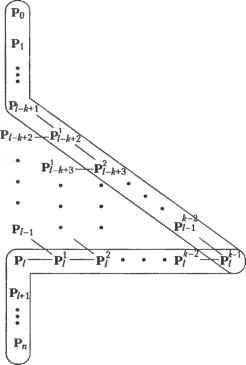 Рис. Ж.2. Схема вычисления Р, Листинг Ж.1. Реализация алгоритма Кокса - де Бура на языке С Cox de Boor(k. t. P. u. 1. R) int k: /* порядок В-сплайна */ Knot *t: /* последовательность узлов */ Point *P; /* задающие точки */ double и: I* значение параметра */ int 1: /* целое число, такое, что t[l] <- u < t[l+l] */ Point *R: /* Р(и) */ Point A[MaxOrder]; int i. j. r: double dl. d2: for(j>=0: j<k: A[j] - P[l-k+l+j]: for(r-=l: r<k: r++) { for(j =k-l: j>-r; j--) { Объединение В-сплайнов Чтобы получить новые задающие точки и узловые значения объединенной кривой, мы предположим, что объединяемые кривые имеют одинаковый порядок. В противном случае перед тем как выполнить объединение, нам придется изменить ту кривую, у которой порядок меньше, придав ей тот же порядок, что и у другой кривой (то есть мы будем находить узловые точки и узловые значения эквивалентной кривой боле высокого порядка). Эта процедура описывается в [38]. Обозначим уравнения первого и второго В-сплайна порядка k как Рж(и) и Р2(м), соответственно. Далее предположим, что Р{(и) определяется задающими точками Oj (i = 0,1,и) с узловыми значениями о, (i = 0, 1,п + к). Аналогичным образом, Р2(ы) определяется задающими точками R, (г = 0, 1,тп) с узловыми значениями Wj (i = 0, 1,m + k). Обратите внимание, что Q - это то же самое, что и Ro (рис. 3.1). 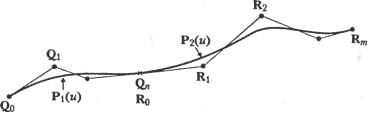 Рис. 3.1. Объединение двух В-сплайнов Тогда уравнения Р^м) и Р2(ы) могут быть записаны следующим образом: P>( ) = EQ,AUM); (3.1) Р2( ) = 1ВДл(ы). (3.2) Теперь определим задающие точки и узловые значения объединенной кривой (без вывода). Мы проверим результат, показав, что объединенная кривая в своих соответствующих частях представляет исходные кривые. Во-первых, множество задающих точек объединенной кривой Р; представляет собой простое объединение множеств задающих точек двух кривых: \ъ (*=0..... R, (z = n+l,. , m+n). Обратите внимание, что R0 не фигурирует в уравнении (3.3), поскольку это то же самое, что и Q . Узловые значения объединенной кривой находятся путем слияния двух наборов узловых значений, после того как всё узлы wt будут сдвинуты так, что w0 будет равняться v +k- Нам известно, что сдвиг всех узлов на одно и то же расстояние не влияет на уравнение кривой, поскольку важность имеет только разность между узловыми значениями. При объединении двух наборов узловых значений некоторые из них, соответствующие точке сопряжения между двумя кривыми, исключаются, так что они будут повторяться только к - 1 раз. Если количество повторений больше, чем к - 1, получившаяся объединенная кривая не может рассматриваться как один В-сплайн и, таким образом, не удовлетворяет соотношению, определяющему число задающих точек, их порядок и количество узловых значений. Процесс получения узловых значений для объединенной кривой иллюстрирует рис. 3.2. Узловые значения wt сдвигаются на расстояние (v +k - w0), так что узловое значение w0 становится равным v +l, и из попарно равных узловых значений v +u v +k и и>и wk t оставляются только (k - 1) узлов от v +l до vn+k. Таким образом, узловые значения, которые будут использоваться для объединенной кривой, находятся, как показано штриховыми прямоугольниками на рис. 3.2, и могут быть выражены следующим образом: к (1-0, ч.*-!* [W,. n + v k-w0 (i = n+k,..., n + m+k). к раз v0 vi vt , vk vk+i v v +i V +t ! к раз vn+k k k+l >*W*i w0 Wl --- к раз Рис. 3.2. Объединение узловых значений Теперь убедимся, что объединенная кривая, которая определяется задающими точками и узловыми значениями, заданными формулами (3.3) и (3.4), совпадает с двумя исходными В-сплайнами в каждой из соответствующих частей. Рассмотрим часть кривой, соответствующую интервалу t (= v ) и t +L (= v +J = vn+2 = ... = = f +4 i). Мы знаем, что N \(u) - единственная функция сопряжения первого порядка, не убывающая в данном диапазоне и. Распространяя эффект NnA(u) (рис. 6.5), мы найдем, что N k+iJl(u), Л/гД ) -> NnJl(u) являются ненулевыми функциями сопряжения порядка к. Таким образом, кривая определяется задающими точками Рп (нч, Рп-&+2. > Рп- Эти задающие точки совпадают с точками 0 -яф Ол-к+2< > Ол- Далее, подмножество узловых значений объединенной кривой, участвующих в вычислении функций сопряжения Nu), Л^.Ды), .... N M(u), будет совпадать со значениями, входящими в Ру(и). Из этого мы можем заключить, что объединенная кривая Р(и) совпадает с Pi (и) для значений и в интервале t и £ +,. К тому же заключению мы придем в случае, когда и находятся меж- ду узловыми значениями, меньшими г„. Таким же образом можно показать, что Р(и) совпадает с Р2(и) при и t +k. Пример 3.1 Два непериодических однородных В-сплайна порядка 4, один из которых определен задающими точками Р Р2, Р3 и Р4, а другой - Oj (= Р3), Q2, Q3 и О^, требуется представить с помощью объединенного В-сплайна. Найти узловые значения объединенной кривой. Решение Кривая В-сплайна, определенная точками Р„ будет иметь узловые значения 00001 1 1 1, а кривая, определенная точками - узловые значения 00001222 2. Чтобы сделать первое узловое значение из второго набора равным последнему узловому значению первого набора, узловые значения второго набора сдвигаются на 1, в результате чего получаются значения 1 1 1 12333 3. После этого два набора узловых значений объединяются, и некоторые из узловых значений, равные 1, удаляются, чтобы они фигурировали только три (то есть k - 1) раза. Соответственно, объединенная кривая будет иметь узловые значения 00001112333 3. Доказательство формулы дифференцирования В-сплайна Чтобы доказать формулу (6.43), сначала докажем справедливость следующего соотношения: К{и)--{г-ц\-1\ (И.1) [Ч+r-i Ч Ч+г Ч+l J Для доказательства (И.1) мы перепишем уравнения (6.32) и (6.33) более удобным образом: ,.,<*>4! ,й'й, (И.2) [О во всех остальных случах и * (и)=N ->{u)+ fti+rStu N(И-3) i+r-1 Ч Ч+r Ч+l Теперь выведем формулу (И.1), рассуждая по индукции. Иными словами, мы покажем, что уравнение (И.1) справедливо при r=k, если установлена его справедливость при r=k- 1. Мы также покажем, что равенство (И.1) выполняется при г =2. В таком случае оно должно выполняться и при г = 3. Повторяя это индуктивное рассуждение с увеличением г, мы можем доказать, что формула (И.1) выполняется для всех г. Первым делом покажем, что равенство (И.1) выполняется при г = 2. Подставляя г= 2 в (И.З), получим Nl3{u) = --Nitl(u)+ N,+U(u). (И.4) Ч+\ Ч 4+2 Ч+l Дифференцирование уравнения (И.4) дает Ni2(u) =---, Ч+\ ~Ч Ь+2 ~Ч+\ что эквивалентно уравнению (И.1) при г =2. Предполагая, что (И.1) справедливо для r=k- 1, имеем Ni.i<-.(u) = (k-2)\--T-t-(и-5) [4+11-2 ~Ч Ч+k-l ~Ci+l J Теперь с помощью уравнения (И.5) нам необходимо показать, что уравнение (И.1) справедливо при г = k. Подставляя г=кв уравнение (И.З) и дифференцируя его по и, получим =-+т^т< >+т^г-< > <и-6> Возьмем выражения Л^4 ,(ы) и iV,., (ы) из уравнения (И.5) и подставим их в уравнение (И.6):
tj+b-i h Теперь перепишем второе слагаемое, прибавив и вычтя член (И.7) tub-\ i+i и затем применив формулу (И.З): 1.1.4-2 ( ) Второе слагаемое u-t, , х £,-i/M -и Л+*-2 ,..-2 ( ) + N,-. -2 ( ) - и-2( )--+1..-2(Ю tub-\ £-2 ,(и)- £-2 Изменим порядок суммирования во втором и третьем слагаемом формулы (И.7): Второе слагаемое + Третье слагаемое = k-2 . . k-2 -Wjm( ) + A+t-1 tul 1 JW.fr)- AW,( ) .+ 2.t-2 . . 1f+* li+2 ti+l = (k-2) = (k-2) Хи-Ли) 1 tj tull tM /,t-i( ) Wl+U ,(a) /;+*-] tM tut tu2 AWj( ) A+t-l tj tuk tM Наконец, добавив этот результат к первому слагаемому в формуле (И.7), получим: (Первое слагаемое) + (Второе слагаемое + Третье слагаемое) = = (1) tj+k-t tj tj+k + (k-2) ti*b-\ tj t,+ b-\ tj tub tj+l Результат идентичен формуле (И.1). Теперь докажем формулу (6.43) с помощью формулы (И.1). Перепишем производную первого порядка от кривой В-сплайна при условии, что значение параметра и находится в интервале t{ и следующим образом: аи ,=о Из формулы (И.1) получаем: tub-i tj i р,<*-ц аи ,=/-*+i ы1-ь+2 4+4-1 - Ч tub ti+i ipi(k-i)Nu) (И.8) Обратите внимание, что мы сократили диапазон суммирования в формуле (И.8), зная, что Ni k+lMi(u) = 0 и A.-i>-i( ) = 0 ПРИ *i tl+l. Замена (i + 1) на у во втором слагаемом формулы (И.8) даст l=/-*+2 (=/-* +2 - I- i=/-*+2 Таким образом, мы имеем = 1Р/-,( ). аи ,=;-*+2 где Подход Пенга к вычислению пересечения NURBS-поверхностей В этом приложении дается пошаговое описание подхода Пенга. К.1. Разбиение Как объяснялось ранее, для каждой из пересекающихся поверхностей необходимо создать непрерывное разбиение, которое затем нужно сохранить в виде квадрантного дерева. Поскольку рациональные (нерациональные) поверхности Безье1 разбивать проще, чем рациональные (нерациональные) поверхности В-сплайнов, мы преобразуем каждую NURBS-поверхность в множество рациональных лоскутов Безье (рис. К.1). 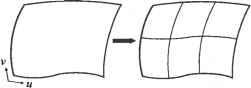 Рис. К.1. Преобразование NURBS-поверхности в рациональные лоскуты Безье После того как это будет проделано, пары рациональных лоскутов Безье, которые могут пересекаться, сохраняются в списке, называемом списком соперников (rival list). Например, на рис. К.2 показано преобразование NURBS-поверхностей S1 и S2 (рис. К.2, а) в четыре рациональных лоскута Безье PI, Р2, РЗ и Р4 и два рациональных лоскута Безье Q1 и Q2 соответственно. Эти рациональные лоскуты Безье сохраняются в квадрантных деревьях (рис. К.2, б). Обратите внимание, что на рис. К.2, а пересечения могут возникать между лоскутами РЗ и Q1 и лоскутами Р4 и Q1. Поэтому данные пары записываются в список соперников (рис. К.2, в). Возможность пересечения двух лоскутов может быть обнаружена путем сравнения минимального размера блоков, каждый из которых едва умещает в себе лоскут. После этого проверяется, являются ли лоскуты, хранящиеся в списке соперников, достаточно плоскими для того, чтобы их можно было аппроксимировать плоскими четырехугольниками. Если какой-либо из лоскутов в списке не явля- 1 Рациональная поверхность Безье получается из поверхности Безье путем введения одно-Родных координат для контрольных точек. ется достаточно плоским, он делится на четыре части. В этом случае квадрантное дерево соответствующей поверхности обновляется с учетом этих новых лоскутов. Также модифицируется список соперников, так что пары, включавшие до разбиения старый лоскут, удаляются,/ а вместо них добавляются пары с новыми лоскутами. 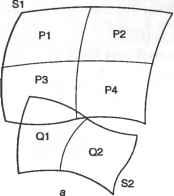  Р1 Р2 РЗ Р4  P3-Q1 P4-Q1 Рис. К.2. Представление рациональных лоскутов Безье в виде квадрантного дерева и его список соперников На рис. К.З показано, как изменяется квадрантное дерево и список соперников, когда лоскут делится на части, поскольку не прошел тест на плоскостность. В данном примере на плоскостность проверяются лоскуты из пары P3-Q1, и лоскут Q1 делится на четыре новых лоскута: Qll, Q12, Q13 и Q14. Здесь мы предполагаем, что лоскут РЗ прошел тест на плоскостность. Таким образом, квадрантное дерево, изображенное на рис. К.2, б, обновляется в соответствии с рис. К.З, б. После этого производится тест на пересечение между новыми лоскутами и РЗ для обновления пары P3-Q1 в исходном списке соперников. Если новые лоскуты располагаются, как показано на рис. К.З, а, то пара P3-Q1 будет заменена на две пары P3-Q11 и P3-Q12 (рис. КЗ, в). 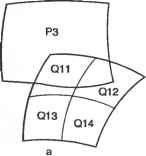 Q1 Q2 Р1 Р2 РЗ Р4 Q11 Q12 Q13 Q14 б РЗ- Q11 P3-Q12 Р4 - Q1~ Рис. К.З. Обновление квадрантного дерева и списка соперников после теста на плоскостность 1 филожение К. Подход Пенга к вычислению пересечения NURBS-поверхностей К.2. Нахождение пересекающихся сегментов Мы получили квадрантные деревья пересекающихся поверхностей и список соперников. Теперь можно приступить к поиску пересекающихся сегментов, начиная с одной из пар в списке соперников. Сначала мы можем взять любую из пар в списке соперников и вычислить сегмент их пересечения (или, точнее, две конечные точки). Для вычисления этих конечных точек мы используем пересечение двух плоскостей, поскольку все лоскуты в списке соперников уже прошли тест на плоскостность. Обозначим эти точки как А1 и А2. Вспомните, что мы всегда находим точные координаты соответствующих точек, когда получаем конечные точки по пересечению двух плоскостей. Конечная точка используется как первоначальное грубое приближение для точного нахождения соответствующей точки путем решения уравнения (7.50). Теперь необходимо найти следующую пару лоскутов, которые дадут сегмент пересечения, соединенный с одним из концов текущего сегмента пересечения. Допустим, что мы ищем точки пересечения от А1 к А2. Соответственно, нам нужно найти пару, которая даст сегмент пересечения с точкой А2. Процедура нахождения следующей пары показана на рис. К.4. Следующая пара, X1-Y2, находится после получения текущей точки пересечения А2 из текущей пары, X1-Y1, следующим образом. Лоскут Y1 Лоскут Y2 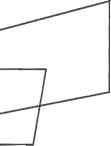 Лоскут Х1 Рис. К.4. Поиск следующей пары Определяется местоположение текущей точки пересечения, в данном случае А2, по отношению к лоскутам текущей пары. Таким образом, А2 находится на границе лоскута Y1 и внутри лоскута XI. Лоскут, полностью содержащий в себе текущую точку пересечения, то есть лоскут XI, используется снова для следующей пары. После этого мы выбираем один из лоскутов, соседствующих с Y1, в качестве второго лоскута для следующей пары. Выбор определяется местоположением текущей точки пересечения относительно Y1. В данном случае мы выбираем правый соседний лоскут, поскольку текущая точка пересечения А2 находится на правой границе лоскута Y1. Затем мы вычисляем точки пересечения для этой новой пары, и для поиска следующей пары роль текущей точки пересечения возьмет на себя другая точка, отличная от А2. гч.С гюлилздспие пересекающихся сегментов Эта процедура завершается, когда точка пересечения достигнет границы одной из пересекающихся поверхностей (рис. К.5). После этого точки пересечения проходятся в обратном порядке, начиная с исходного сегмента пересечения. Можно считать, что текущая кривая пересечения получена полностью, если она превращается в замкнутый контур или пересекается с одной из поверхностей по двум граничным кривым. Мы можем также найти остальные кривые пересечения, выполнив поиск точек пересечения от одной из пар в списке соперников, которая не участвовала в вычислении уже полученных кривых пересечения. Так, если мы не оставим в списке соперников ни одной пары, которая бы не участвовала в вычислении какой-либо кривой, то мы тем самым найдем все кривые пересечения. 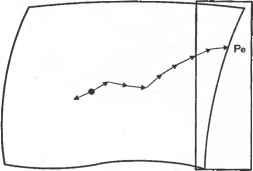 Рис. К.5. Обратный поиск Формулировка системных уравнений конечноэлементного анализа на базе основного дифференциального уравнения В разделе 8.2 мы рассматривали формулировку и решение системных уравнений конечноэлементного анализа непосредственно на основе интегрального уравнения, описывающего условие равновесия решаемой задачи. Однако большинство инженеров знакомы с уравнениями равновесия, выраженными в виде дифференциальных уравнений. Например, уравнения равновесия для задач, связанных с распространением тепла, вибрацией и потоком жидкости, обычно выражены в дифференциальной форме. В этом приложении мы опишем использование метода взвешенных остатков как одного из методов формулировки уравнений конечноэлементного анализа на базе основного дифференциального уравнения1. Метод взвешеюгых остатков (method of weighted residuals) - это численный метод получения приближенных решений дифференциальных уравнений. Он состоит из двух шагов. Сначала выбирается приближенное решение, удовлетворяющее дифференциальному уравнению и его геометрическим граничным условиям. Приближенное решение обычно дается в виде линейной комбинации известных функций с неизвестными коэффициентами. Эти известные функции эквивалентны функциям формы, а неизвестные коэффициенты эквивалентны смещениям узловых точек. Когда это приближенное решение подставляется в дифференциальное уравнение и граничные условия, получается ошибка, или остаток. Соответственно, решение исходного дифференциального уравнения эквивалентно устремлению этого остатка к нулю в некотором усредненном смысле во всей области решений. Отсюда возникают интегральные уравнения. На втором шаге интегральные уравнения решаются относительно неизвестных коэффициентов, и таким образом получается приближенное решение. Рассмотрим каждый шаг несколько более подробно. Прежде всего будем считать, что основное дифференциальное уравнение имеет вид Вариационный метод основан на минимизации соответствующего функционала, эквивалентного дифференциальному уравнению равновесия, и может быть использован для формулировки уравнений конечноэлементного анализа из основного дифференциального уравнения. Однако метод взвешенных остатков можно использовать даже в том случае, когда функционала, эквивалентного дифференциальному уравнению равновесия, не существует. Формулировка уравнении с помощью вариационного метода представлена в [166] и [145]. 1(ф)-/=0 (Л.1) в области континуума D. Допустим также, что граничные условия таковы: Ф = Ф на В. Здесь ф - это зависимая переменная, относительно которой ищется решение,/- известная функция независимых переменных, L - линейный или дифференциальный оператор, а В - граница области D. Начнем с того, что зададимся приближенным решением фа: Ф = Фв =\tcigi, (Л.2) где С, - это неизвестные коэффициенты, относительно которых ищется решение, agj - принятые нами известные функции независимых переменных. Подстановка (Л.2) в (Л.1) дает ненулевое значение 1(ф„ )-/, поскольку ф„ является приближенным решением. Обозначим это ненулевое значение как остаток R, выражаемый формулой R = L(<pa)-f. (Л.З) Чтобы минимизировать R во всей области решений, определим взвешенное среднее значение, которое должно стремиться к нулю во всей области: fRWidD = l[L(4>a)-f]WidD = 0, (Л.4) где W, - это весовые коэффициенты. Подставляя в уравнение (Л.4) п различных весовых коэффициентов, мы можем получить систему из п уравнений, из которой можно определить неизвестные С, (i= 1, 2.....п). Эти весовые коэффициенты могут быть выбраны по различным критериям. В методе Галеркина, например, в качестве W; используются известные функции gi из уравнения (Л.2). В этом случае система уравнений для метода Галеркина принимает вид JD = j [L(9a)-/]gD = 0 f = l,2.....п. (Л.5) В примере Л.1 мы покажем, как использовать метод Галеркина для формулировки уравнений конечноэлементного анализа в задаче распространения тепла. Применение метода Галеркина к решению других типов задач описывается в [145]. Пример Л.1 Рассмотрим одномерную задачу распространения тепла, представленную на рис. Л.1, я: температура стержня изменяется только в осевом направлении. Смоделировав стержень в виде совокупности линейных элементов с двумя узлами (рис. Л.1, б), вывести системные уравнения конечноэлементного анализа с использованием метода Галеркина. Теплопроводность материала равна k, коэффициент конвективного теплообмена равен h, окружающая температура равна Та, а интенсивность теплообразования в единице объема равна Q. Предположим, что излучательным теплообменом можно пренебречь. 1 ... 25 26 27 28 29 |
|
| |||