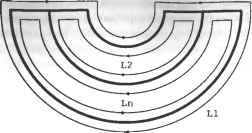Рис. В.22. Результат после шага 5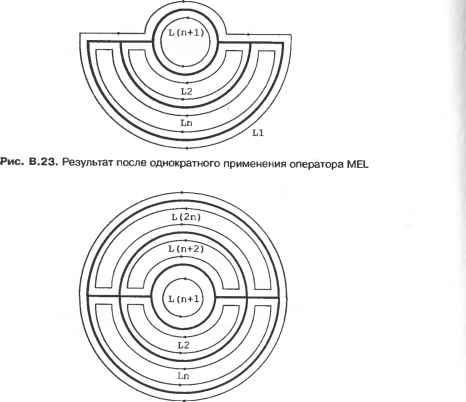

Рис. В.24. Результат после применения оператора MEL п раз

В.2.3. Создание примитивов

Как вы помните, большинство систем твердотельного моделирования позволяют пользователям получать объемы простых форм, на основе которых можно моделировать более сложные объемы. Этот метод работает, поскольку процедуры, используемые для создания этих примитивов, заранее заданы, и примитивы могут оыть сгенерированы в любом желаемом размере в соответствии с параметрами,

заданными пользователем. Эти процедуры обычно состоят из операторов Эйлера, производящих трансляционное или вращательное заметание, поскольку большинство примитивов можно создать с помощью этих функций моделирования. На самом деле операторы Эйлера просто незаменимы для хранения примитивов в системах твердотельного моделирования. Например, в листинге В.2 приведена процедура создания примитивного параллелепипеда с параметрами W, D и Н, показанного на рис. В.25.

г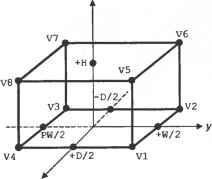

х

Рис. В.25. Параметры и система координат для параллелепипеда

Листинг В.2. Процедура создания параллелепипеда

Body *Create Block (W. D. H)

double W. D. H:

Body *B: Shell *S.

Loop *L1. *L2. *L3. *L4. *L5. *L6: Edge *E1. *E2. *E3. *E4. *E5. *E6: Vertex *V1. *V2. *V3. *V4. *V5. *V6. *V7. *V8:

В - malloc(sizeof(Body));

MEVVLSCB. &E1. &V1. &V2. &L1. &S. D/2. W/2. 0. -D/2. -W/2. 0):

MEV(B. LI. V2. &E2. &V3. -D/2. -W/2. 0):

MEV(B. LI. V3. &E3. &V4. D/2. -W/2. 0):

MEL(B. LI. V4. VI. &E4. &L2):

MEV(B. LI. VI. &E5. &V5. D/2. W/2. H):

MEV(B. LI. V2. &E6. &V6. -D/2. W/2. H):

MEV(B. LI. V3. &E7. &V7. -D/2. -W/2. H):

MEV(B. LI. V4. &E8. &VB. D/2. -W/2. H):

MEL(B. LI. V5. V6. &E9. &L3):

MEL(B. LI. V6. V7. &E10. &L4):

MEL(B. LI. V7. V8. &E11. &L5):

MEL(B. LI. V8. V5. &E12. &L6):

return(B):

Для реализации этих трех основных функций моделирования мы применили операторы Эйлера в надлежащей последовательности. Приведенный ниже пример являет собой дальнейшую демонстрацию того, что любую функцию моделирования можно реализовать с помощью операторов Эйлера.

Пример В.1

Покажите, как применить последовательность операторов Эйлера для реализации операции моделирования, которая разделит шестигранник (рис. В.26, а) на два шестигранника (рис. В.26, е).

TL, 4 г mve -о-

MZEV

8 f MEL

КЕМН МРКН

Рис. В.26. Реализация функции моделирования с помощью операторов Эйлера Решение

Необходимо последовательно вызвать следующие операторы Эйлера (рис. В.26).

□ Ребра разбиваются надвое операторами MVE (рис. В.26, б). Этот оператор применяется четыре раза.

U К каждой вершине, созданной на предыдущем шаге, применяется оператор MZEV, что приводит к результату, изображенному на рис. В.26, в. Оператор MZEV также применяется четыре раза.

□ При помощи оператора MEL соединяются новые вершины, созданные на предыдущих шагах, и создаются грани. Оператор MEL применяется восемь раз, в результате чего создается восемь ребер и восемь вершин (рис. В.26, г). Обратите внимание, что четыре грани в середине не содержат в себе областей.

□ Ребра нулевой длины уничтожаются оператором KEL (рис. В.26, д). Когда ребро уничтожается оператором KEL, две грани, для которых это ребро было общим, объединяются. Оператор KEL применяется восемь раз, в результате чего остается одно связующее ребро нулевой длины (рис. В.26, д).

□ Связующее ребро удаляется оператором КЕМН. Так как КЕМН превращает одно из двух колец, связанных с удаляемым ребром, в кольцо отверстия, необходимо преобразовать его во внешнее кольцо с помощью оператора МРКН. Как было сказано выше, МРКН обнаружит наличие двух несвязанных оболочек и сохранит разделенные шестигранники в двух отдельных оболочках (рис. В.27, е).

Объем А

Объем В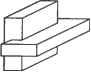

✓ х \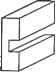

Объединение Пересечение Разность

Рис. Г.1. Пример булевской операции

Грань объема Ксегмент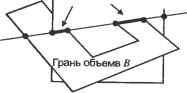

Кривая пересечения

Рис. Г.2. Определение ксегмента

В зависимости от типов уравнений, используемых для представления каждой поверхности, можно использовать различные методы вычисления кривых пересечения, как описано в главе 7. Кроме того, конечные точки ксегмента находятся по точкам пересечения кривой пересечения с ребрами граней, как описано в главе 6.

2. Ксегменты, полученные на шаге 1, наносятся на соответствующие грани объемов А и В (рис. Г.З). Каждый ксегмент добавляется как новое ребро соответствующей грани каждого объема с помощью операторов Эйлера, так что разделение граней учитывается автоматически. Операторы Эйлера выбираются в зависимости от расположения ксегмента относительно грани, на которую он должен быть нанесен. Есть пять возможных вариантов расположения (рис. Г.4). На рис. Г.4, а изображена ситуация, в которой новое ребро совпадает с существующим; здесь никаких действий не требуется. На рис. Г.4, б два конца нового ребра совпадают с существующими вершинами, но само ребро не совпадает с существующими ребрами; в этом случае необходимо применить оператор MEL На рис. Г.4, в один конец нового ребра совпадает с существующей вершиной, а другой расположен внутри грани; в этом случае применяется оператор MEV. На рис. Г.4, г оба конца нового ребра находятся внутри грани; в этой ситуации мы действуем операторами MEWLS и КРМН. Здесь оператор КРМН преобразует кольцо, созданное оператором MEWLS, в кольцо отверстия, принадлежащее внешнему кольцу грани. Одновременно он устраняет избыточную оболочку, если кольцо, которое преобразовывается в кольцо отверстия, было связано с отдельной оболочкой. На рис. Г.4, д два конца нового ребра связаны с разными кольцами на грани; в этом случае применяется оператор МЕКН. Из этих объяснений мы можем заключить, что каждый ксегмент можно нанести на соответствующую грань каждого из объемов автоматически, если можно автоматически определить его положение по отношению к этой грани. Для этого необходимо проверить, где лежат конечные точки нового ребра: внутри, снаружи или на границе грани. Такая проверка называется тестом на вхождение (in/out test).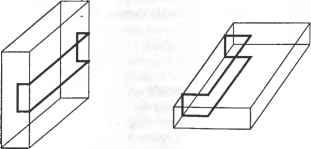

Объем А после модификации Объем В после модификации

Рис. Г.З. Добавление новых граней к объемам Л и Б

Пошаговый алгоритм реализации булевской операции

Алгоритм выполнения булевских операций, используемый в SNUMOD, можно описать следующим образом для случая операции, изображенной на рис. ГЛ. 1. Вычисляются кривые пересечения всех граней объема А и всех граней объема В; объемы А и В показаны на рис. Г.1. Затем находятся фрагменты каждой из кривых пересечения, лежащие внутри двух граней, которые пересекаются по данной кривой (рис. Г.2). Далее такие фрагменты будут называться ксег-ментами (xegments). Вычисление кривой пересечения между двумя гранями - сложная задача. Однако оно является важным аспектом определения эффективности и устойчивости булевской операции.

Приложение Г. Пошаговый алгоритм реализации булевской операции

а б в г а

Рис. Г.4. Возможное расположение ксегментв по отношению к соответствующей грани

3. Грани объема А классифицируются по их расположению относительно объема В. Иными словами, для каждой грани определяется, расположена ли она внутри, снаружи или на граничной поверхности объема В. Грани объема В классифицируются таким же образом по отношению к объему А.

Классификация требует большого объема вычислений, поэтому мы будем избегать ее, если результат можно вывести из результата для соседних граней. К счастью, группы граней одного объема могут иметь одинаковое положение по отношению к другому объему. На рис. Г.5 грани, принадлежащие к каждой из групп, имеют одно и то- же положение относительно другого объема (то есть грани в группе А, находятся вне объема В, грани в группе Вх находятся внутри объема А). Эти группы также разделены новыми ребрами, полученными из ксегментов.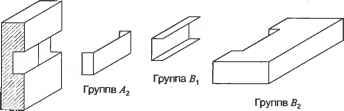

Группа А:

Рис. Г.5. Группы граней

Таким образом, грани; принадлежащие группе, можно определить путем обхода соседних граней, начиная с любой грани в группе, без пересечения ксре-бер (xedges) - новых ребер, полученных из ксегментов. Будем искать грани, принадлежащие одной группе, начав обход с грани, которая заштрихована на рис. Г.5. Сначала из всей совокупности соседних граней отбираются только те, которые не имеют общих ксребер с заштрихованной гранью. Затем процедура повторяется: каждая из отобранных ранее граней используется в качестве вторичной начальной грани, и обнаруженные на данной итерации грани Добавляются к отобранному множеству. Процесс останавливается, когда каждая грань из отобранного множества побывает в роли вторичной исходной грани. В данном примере будут отобраны грани из группы А,. После этого в качестве вторичной исходной грани будет выбрана любая из граней, не принадлежащих к группе А{, тот же самый процесс будет повторен для нахождения граней, принадлежащих к группе А2. Если какая-либо грань не принадлежит ни к А ни к Л2, то далее находятся грани группы Л3 (которые не

Пошаговый алгоритм реализации булевской операции

существуют в данном примере). Такой же процесс применяется к объему В, в результате чего получаются группы граней Вх и В2 (рис. Г.5).

После того как грани объемов Аи В будут разделены на группы, необходимо определить положение каждой группы граней по отношению к противоположному объему. В качестве примера рассмотрим метод для группы At. Остальные группы можно обрабатывать так же. Сначала произвольно выбирается одно из ксребер, образующих внешнюю границу группы Аь и обозначается как Хс (рис. Г.6). Любая из граней группы Л имеющая Хе одним из своих ребер, обозначается Fa, а грань объема В, делящая ребро X,. с Fa, обозначается Fb. Затем находятся векторы Na и Nb внешних нормалей к граням Fa и Fb, а такж<$ тангенциальный вектор Т в любой точке X,. (рис. Г.6). Тангенциальный вектор Т имеет направление против часовой стрелки, чтобы он был согласован с направлением внешнего кольца La грани Fa при взгляде снаружи. Наконец, классификация группы Л, по отношению к объему В находится из значения (Na Т) Nb следующим образом. Группа Л, находится вне объема В, если это значение положительно, внутри - если значение отрицательно, и на поверхности объема, если это значение равно нулю. Если выясняется, что группа Л находится на поверхности объема В, она далее классифицируется как ON SAME (если Na и Nb имеют одно и то же направление) или ON OPPOSITE (если Na и Nb направлены противоположно).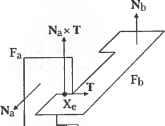

Рис. Г.6. Классификация групп граней

4. Группы граней отбираются в соответствии с конкретной булевской операцией. Правила отбора групп определяет табл. Г.1. Мы объясним, как использовать эти правила для операции объединения, а для прочих операций они используются точно так же. Для операции объединения табл. Г.1 показывает, что нам необходимо отобрать элементы О и О(Х) в столбце Объединение . Это означает, что мы должны отобрать группы объема Л, находящиеся вне' объема В, группы объема В, находящиеся вне объема Л, и группы объема Л, классифицированные как ON SAME (или группы ON SAME объема В). Символы О(Х) и Х(О) в табл. Г.1 подразумевают, что элемент объема Л соответствует элементу объема В, и что данный элемент должен быть отобран лишь единожды. Если мы применим это правило к группам граней на рис. Г.5, мы выясним, что для операции объединения будут отобраны группь

Приложение Г. Пошаговый алгоритм реализации булевской операции

А\ иВ2. Правила для операций разности и пересечения вы можете проверить, применяя их к группам граней на рис. Г.5.

Таблица Г.1. Группы граней, отбираемые для булевских операций

5. По результатам, полученным на шаге 4, ненужные группы граней удаляются из каждого объема. Для примера с операцией объединения из объемов А и В удаляются соответственно группы А2 и В\. Форму объемов Аи В после удаления ненужных групп граней илюстрирует рис. Г.7. Сложной топологической операции, необходимой для создания объема, можно избежать, удалив ненужные группы граней из исходного объема, вместо того чтобы создавать новый объем из отобранных групп граней. Как упоминалось ранее, подходы, изложенные в работах [132, 115], требуют этой топологической операции.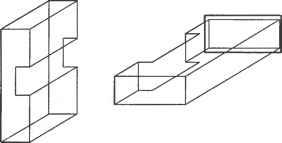

Рис. Г.7. Объемы после удаления ненужных групп граней

В качестве примера рассмотрим удаление группы граней А2 из объема А. Грани группы А2 можно удалить путем уничтожения ребер Ei и Е2 (рис. Г.8). В общем случае грани, принадлежащие группе, удаляются путем уничтожения всех их ребер, кроме ксребер. Ксребра уничтожать не следует, поскольку они также являются граничными ребрами других групп граней, которые сохраняются. Ребро Е, удаляется оператором Эйлера KEL, который также объединяет грани F) и F2 (рис. Г.9, а). Аналогичным образом с помощью оператора KEL удаляется ребро Е2 (рис. Г.9, б). Теперь геометрическая информация,

- wwit wpnin uiirijULirin WfJ№OU\Uri ииОЦПП

хранимая для грани F не имеет смысла, и на следующем шаге используется только информация о ее внешнем кольце.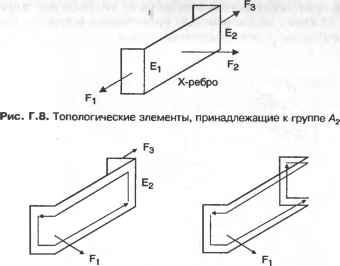

в б

Рис. Г.9. Процедура удаления Е, и Е2

6. Два объема, полученные на шаге 5, склеиваются по общей границе (рис. Г. 10). Ту же процедуру склеивания необходимо применить к другим группам граней при использовании операторов пересечения и разности.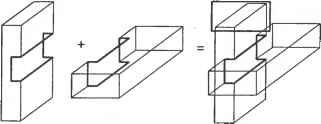

Рис. Г. 10. Создание объема путем склеивания

Для примера, изображенного на рис. Г. 10, процедура склеивания выполняется следующим образом. Во-первых, определяются восемь пар совпадающих вершин и восемь пар совпадающих ребер, и пара вершин соединяется операторами КРМН и МЕКН. Как объяснялось ранее, два объема будут объединены оператором КРМН и сохранены в одной оболочке. Более того, одно из двух общих граничных колец станет кольцом отверстия для другого в результате применения оператора КРМН. Оператор МЕКН соединяет пару совпадающих вершин путем присоединения кольца отверстия к внешнему кольцу. Оставшиеся семь пар вершин соединяются путем семикратного применения оператора MEL (рис. Г. 11). Во-вторых, каждая пара вершин, соединенных ребром

нулевой длины, удаляется оператором KZEV. Этот оператор применяется восемь раз, поскольку имеется восемь вершин, соединенных ребрами нулевой длины. Обратите внимание, что множественные ребра и вырожденное кольцо до сих пор существуют для каждого ребра, на что указывает жирная линия на рис. 7.11. Наконец, восьмикратным применением оператора KEL удаляются множественные ребра и вырожденные кольца.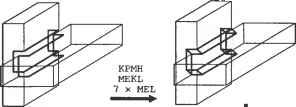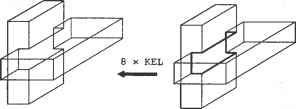

Рис. Г.11. Пошаговая иллюстрация процедуры склеивания

7. Далее определяется, имеет ли полученный объем множественные несвязанные оболочки. Этот шаг необходим, поскольку булевская операция может привести к появлению нескольких объемов, что демонстрирует рис. Г. 12.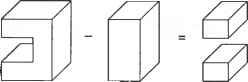

Рис. Г. 12. Булевская операция, приводящая к появлению нескольких объемов

Структура данных и топологические операторы для немногообразных систем моделирования

Д.1. Структура данных

В разделе 5.3.2 мы представляли объем в виде трех таблиц - грани, ребра и вершины. Можно представить себе хранение списков топологических элементов немногообразной модели аналогичным способом. Такой подход, предложенный в [109], иллюстрирует рис. Д.1. Объект, в данном случае пирамида со слоистой гранью и свободным ребром, состоит из объема, соответствующего пирамиде,! грани, соответствующей слоистой грани, и ребра, соответствующего свободному! ребру. Объем определяется оболочкой, окружающей объект, а оболочка снова определяется списком поверхностей (см. таблицу граней в разделе 5.3.2). Далее, с каждой гранью связаны кольца, и каждое кольцо имеет список ребер (см. таблицу ребер в разделе 5.3.2). Аналогичным образом, каждое ребро имеет список вершин (см. таблицу вершин в разделе 5.3.2). Структура данных, представленная на рис. Д.1, а, представляется весьма компактной и четкой, поскольку она является простым расширением структуры данных на случай немногообразных моделей. Однако эта структура не дает достаточно информации для получения сведений о смежности топологических элементов. Например, при добавлении к модели новой грани (рис. Д.1, а) мы должны выяснить отношения смежности между гранями. Если добавленная грань создает новую оболочку с существующими гранями, необходимо определить эту оболочку и добавить ее, изменив оболочку 5[ в структуре данных, показанной на рис. Д.1, б. Чтобы можно было определить оболочку, образуемую гранями, необходимо иметь информацию о смежности граней.

Разработано несколько подходов к описанию немногообразной топологии, в особенности информации о смежности. Наиболее значительная работа была проделана Вейлером, который ввел структуру радиальных ребер для представления немногообразных топологий [156]. В случае многообразных твердотельных моделей информация о смежности хранится в виде двух типов циклического упорядочивания (то есть цикл грань - ребро и цикл вершина - ребро ). Цикл грань - ребро - это список ребер для каждой грани или кольца, а цикл вершина - ребро - список связанных ребер, сходящихся в заданной вершине. Посмотрев на структуру полуребер и структуру крыльевых ребер в разделе 5.3.2, можно убедиться, что эти сведения о циклах хранятся прямо или косвенно. Между тем, для представления немногобразной модели общего вида необходимо

задать три типа циклов: кольцевой, радиальный и дисковый. Кольцевой цикл (рис. Д.2, а) соответствует циклу грань - вершина в многообразных твердотельных моделях. Радиальный цикл, показанный на рис. Д.2, б представляет собой цикл граней, соединенных с определенным ребром. Эта информация не является необходимой в многообразной модели, поскольку ребро всегда принадлежит двум граням. Однако в немногообразных моделях ребро может одновременно принадлежать более чем двум граням, и они должны быть заданы явно. Дисковый цикл, изображенный на рис. Д.2, в, напоминает цикл вершина-ребро в многообразных твердотельных моделях. Однако в немногообразных моделях вершина может иметь несколько дисковых циклов. Например, вершина V на рис. Д.З, а к б имеет три дисковых цикла, каждый из которых принадлежит своей оболочке.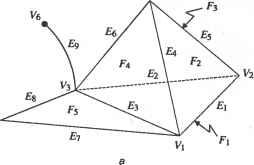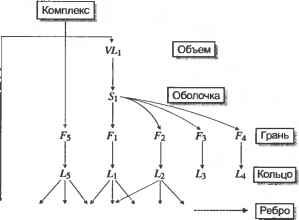

£9 £g £7 £3 Е] £2 £4 Es

/\/\

v6 v3 v5 -----------------------

Вершина

Рис. Д.1. Представление немногообразной модели с помощью списков топологических элементов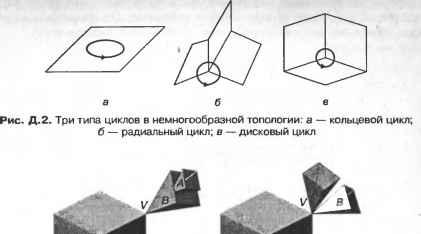

а б

Рис. Д.З. Топологически различные модели

Представление радиальных ребер, предложенное Вейлером [156], является первым полным немногообразным представлением для моделирования границ, в котором топологическая смежность представлена в явном виде. С ее помощью можно представить радиальный цикл и кольцевой цикл, но она не хранит в явном виде дисковый цикл вокруг вершины. Хотя информация о смежности у вершины в ограниченном числе случаев может быть получена из другой топологической информации, структура радиальных ребер не всегда позволяет получить правильную информацию такого рода из топологических данных. Более того, топологически различные модели, изображенные на рис. Д.З, представляются в структуре радиальных ребер одной и той же топологией. Чтобы обойти эту трудность, в [60] было предложено вершинное представление, с помощью которого можно выразить и дисковые, и радиальные, и кольцевые циклы. Здесь мы опишем только представление радиальных ребер, поскольку прочие представления можно рассматривать как его расширения. Описания других представлений можно найти в [161].

Базовыми топологическими элементами, с помощью которых представляется немногообразная модель в структуре данных радиальных ребер, являются модель, регион, оболочка, грань, кольцо, ребро и вершина (рис. Д.4). Модель эквивалентна комплексу, показанному на рис. Д.1, б, и означает просто множество всех задействованных регионов. Регион эквивалентен объему, показанному на рис. Д.1, б, и, таким образом, окружен одной или несколькими оболочками. Регион окружен несколькими оболочками, когда внутри него имеются пустоты. В представлении радиальных ребер одиночный твердотельный объект имеет две оболочки - одна внутренняя, а другая внешняя, имеющая бесконечные размеры Оболочка - это

Приложение Д. Структура данных и топологические операторы

ориентированная граничная поверхность региона, и она имеет то же значение, что и на рис. Д.1, б. Такие топологические сущности, как грань, кольцо, ребро и вершина, имеют тот же смысл, что и в многообразном представлении.

Модель

Оболочка [

Вхождение грвни

Вхождение кольца

Грань J

Вхождение ребра U-► Ребро

Вхождение вершины -► Вершина \

Рис. Д.4. Топологические элементы в представлении радиальных ребер

Рисунок Д.4 показывает, что связи между базовыми топологическими сущностями задаются косвенно через четыре дополнительных топологических элемента: вхождение грани, вхождение кольца, вхождение ребра и вхождение вершины. Это аналогично введению полуребер для косвенного задания связей между кольцами, ребрами и вершинами (см. раздел 5.3.2). Вхождение грани (face-use) - это один из двух вариантов использования грани, или одна из двух ее сторон. Таким образом, оболочка, окружающая внешнюю или внутренню область объема, определяется набором связанных вхождений граней. Вхождение грани, или использование грани оболочкой, имеет определенную ориентацию по отношению к геометрии грани, и эта ориентация противоположна ориентации сопряженного ему вхождения данной грани. Каждое из двух вхождений грани становится элементом каждой из двух оболочек, обращенных к данной грани. В случае сотовой структуры без замкнутого объема, как на рис. Д.5, эти сопряженные вхождения грани принадлежат одной и той же оболочке. В данном примере список вхождений граней fiii- fu2- fu5- fu6- fu4- fu3 образует оболочку. Вхождение грани ограничено одним или несколькими вхождениями кольца, так как грань окружена кольцами. Вхождение кольца (loop-use) - это один из вариантов использования кольца, связанный с одним из двух вариантов использования грани, и оно имеет ориентацию по отношению к соответствующему вхождению грани, что определяет ее внутреннюю или внешнюю границу (см. рис. Д.5). Вхождение кольца определяется списком вхождений ребер. Вхождение ребра (edge-use) - это граничный сегмент кривой на вхождении кольца, принадлежащего вхождению грани, и оно представляет использование ребра данным вхождением кольца или, в случае

Д.1. Структура данных

каркасного ребра, вершинами его конечных точек. Ориентация вхождения ребра определяется вхождением начальной вершины, как и для полуребер. Вхождение вершины (vertex use) - это структура, представляющая смежное использование вершины ребром в качестве конечной точки, кольцом в случае одновершинного кольца или оболочкой в случае одновершинной оболочки.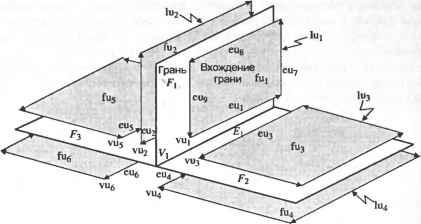

Рис. Д.5. Использование дополнительных топологических элементов для указания

смежности

Некоторые вырожденные ситуации указаны пунктирными связями на рис. Д.4. Во-первых, прямое соединение оболочки и списка вхождений ребра допускает существование оболочки, представляющей собой каркас. Аналогичным образом, соединение оболочки и вхождения вершины допускает существование оболочки, состоящей из одной вершины. Изолированная точка в немногообразном представлении хранится как независимая оболочка. Кроме того, прямое соединение вхождения кольца и вхождения вершины позволяет хранить изолированную точку, находящуюся на грани, в виде кольца отверстия этой грани, что дает возможность представить свободное ребро, исходящее из некоторой точки на грани. Немногообразные модели смешанной размерности можно обрабатывать, интерпретируя элементы меньшей размерности как вырожденные вхождения граней и храня эти вхождения в списке вместе с другими вхождениями граней, принадлежащими той же оболочке.

Теперь поясним, как в структуре радиальных ребер представляются кольцевой и радиальный циклы. Прежде всего, кольцевой цикл задается просто списком вхождений ребер для каждого вхождения кольца. Например, вхождение кольца luj на рис. Д.5 несет в себе список вхождений ребер eut - eu7 - eu8 - eu9. Для задания радиального цикла каждое вхождение ребра имеет два указателя, указатель сопряженности и радиальный указатель (рис. Д.6). На рис. Д.6 изображен вид сотовой структуры, представленной на рис. Д.5, в поперечном сечении. По рис. Д.6 видно, что указатель сопряженности вхождения ребра - это указатель на вхождение ребра на обратной стороне грани, а радиальный указатель указывает на вхождение ребра, которое принадлежит вхождению грани, смежному в радиаль-

Приложение Д. Структура данных и топологические операторы

ном направлении с вхождением грани заданного вхождения ребра. Благодаря этим указателям можно полностью радиально упорядочить грани вокруг ребра, отслеживая указатели от любого вхождения ребра. Как упоминалось ранее, в представлении радиальных ребер дисковый цикл не хранится в явном виде. Однако цикл вершина-ребро хранится, как и в многообразном представлении, в виде списка вхождений вершин для каждой вершины. Хранение списка вхождений вершин эквивалентно хранению вхождений ребер, поскольку каждое вхождение вершины связано с вхождением ребра, и поэтому эквивалентно хранению цикла вершина - ребро . Например, вершина VI на рис. Д.5 хранит список вхождений вершин vui - vu2 - vu3 - vu4 - vu5 - vu6. Обратите внимание, что вхождения вершин перечислены без значительного упорядочивания. Именно поэтому две различные модели, показанные на рис. Д.З, имеют одну и ту же структуру в представлении радиальных ребер.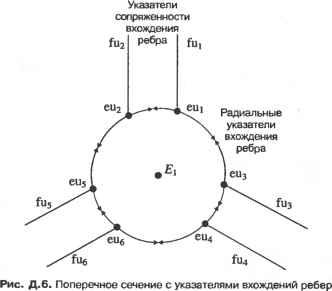

По рис. Д.4 можно заметить, что такие базовые топологические элементы, как грань, кольцо, ребро и вершина, являются избыточными, поскольку вся необходимая информация о них хранится в элементах их вхождений. На самом деле не обязательно иметь прямое представление граней, колец, ребер и вершин как таковых - представления их вхождений достаточно, чтобы указать их положение в модели. Однако с точки зрения системной архитектуры удобнее, когда программисты, использующие операторы для манипуляции структурами данных, имеют дело с более интуитивными понятиями базовых топологических элементов, а не с топологическими вхождениями этих элементов. Это одно из нескольких оправданий для того, чтобы включать в представление такие избыточные элементы, как грани, кольца, ребра и вершины. Это рассмотрение структуры Данных радиальных ребер станет яснее, если вы познакомитесь с детальной реализацией этой структуры в [156].

д./. операторы для манипулирования топологией

Д.2. Операторы для манипулирования топологией

По аналогии с операторами Эйлера, используемыми для манипулирования топологическими элементами в многообразных моделях, были предложены операторы, позволяющие манипулировать топологическими данными в немногообразных моделях [157]. Однако эти операторы не унаследовали полезных свойств операторов Эйлера, поскольку в их основе не лежало уравнение, подобное формуле Эйлера-Пуанкаре. Как вы помните, формула Эйлера-Пуанкаре устанавливает связь между количествами различных топологических элементов многообразной модели. Возможно, вы скептически относитесь к вопросу существования аналогичной формулы для немногообразной модели, принимая во внимание гибкость ее топологии. Однако Масуда с коллегами [109] обобщили формулу Эйлера-Пуанкаре на случай немногообразной модели следующим образом:

u e + (/ r) (V yA +Vc) = C-C +СС, (Д.1)

v - количество вершин; е - количество ребер; / - количество граней;

г - количество колец, или отверстий, в гранях;

V - количество замкнутых объемов во всех комплексах, или просто несвязных объектах1;

Vh - количество отверстий, или проходов через объемы;

Vc - количество полостей, или пустот, в объемах;

С - количество комплексов, или несвязных объектов;

С/, - количество отверстий, или проходов через объекты;

Сс - количество полостей, или пустот, в объектах. Выражение (Д.1) можно проверить на модели, изображенной на рис. Д.1, а. В этой модели v = 6, е = 9,/= 5, г= 0, V= 1, Vh = 0, Ve = 0, С = 1, Ch = 0 и Сс = 0. Подстановка этих значений в выражение (Д.1) дает 6-9 +(5-0)- (1-0 + 0) = = 1-0 + 0, что удовлетворяет уравнению.

Мы можем также показать, что формула Эйлера-Пуанкаре, приведенная в уравнении (5.1), является просто частным случаем уравнения (Д.1). Поскольку любой несвязный объект имеет один объем в многообразной интерпретации, мы знаем, что V = С, Vh = Ch и Vc = Сс. Подставляя это в уравнение (Д.1), получаем

v-e + if-r) = 2(V-V +VC). (Д.2)

Число оболочек s равняется сумме количества объемов Уи количества пустот Vc, поэтому (Д.2) можно переписать следующим образом:

v-e + (f-r) = 2(s-Vh). (Д.З)

Любой несвязный объект считается одним комплексом, и каждый комплекс может состоять из нескольких объемов и свободных ребер. Комплекс эквивалентен модели в представлении радиальных ребер.

Следовательно, уравнение (Д.З) - это то же самое, что и уравнение (5.1), поскольку г и V/, имеют такой же смысл, что hup в уравнении (5.1).

Когда связь между топологическими элементами в немногообразной модели установлена, как в уравнении (Д.1), мы можем определить минимальный набор операторов, необходимых для манипулирования ими. Поскольку формула (Д.1) определяет плоскость в 10-мерном пространстве с координатами (гл е, /, г, V, Vh, Vc, С, Ch, Сс), имеется 9 независимых базисных векторов. Таким образом, для описания любого объекта в немногообразной топологии достаточно иметь 9 операторов и соответствующих им обратных операторов. Один из возможных минимальных наборов, определенный в [109], иллюстрирует рис. Д.7. Хотя девяти операторов достаточно для создания любого объекта, на практике можно достичь большей эффективности, если добавить еще несколько операторов. Как вы помните, в разделе 5.3.3 мы ввели семь операторов Эйлера, хотя для создания многообразной модели достаточно пяти.

Рис. Д.7. Минимальный набор операторов

Точно так же, как команды моделирования высокого уровня реализованы в системах твердотельного моделирования с помощью операторов Эйлера, команды немногообразных систем моделирования реализуются путем последовательного выполнения соответствующих операторов. На рис. Д.8 показано, как с помощью предложенных операторов, перечисленных на рис. Д.7, создается примитивный параллелепипед. Все прочие команды моделирования реализованы аналогично. На самом деле команды, доступные в немногообразных системах моделирования, выглядят точно так же, как команды обычных системах твердотельного мо-

делирования, так что пользователь может и не заметить разницы в их использовании. Единственным различием будет область значений представимого объекта и, соответственно, хранимые в нем данные.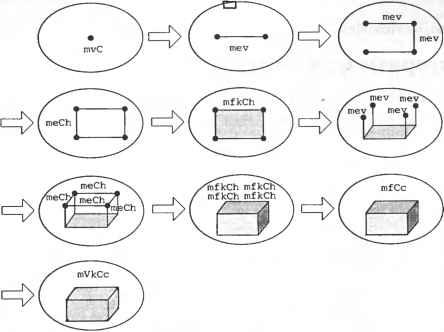

Рис. Д.8. Создание примитивного параллелепипеда с помощью операторов, предложенных Масудой и др.