мы1 (в р-версии), тем точнее оказывается решение, но тем дороже оно стоит с вычислительной точки зрения. Различные виды конечных элементов рассматриваются в разделе 8.3. Другая проблема - построение сетки, особенно для объекта сложной геометрии. Создание трехмерных сеток конечных элементов обычно представляет собой трудоемкий и кропотливый процесс. Сейчас ведутся активные разработки систем автоматизированного построения сеток, которые могли бы подключаться к системам геометрического моделирования. Такие системы позволили бы полностью интегрировать средства САМ и CAE. Краткий обзор на данную тему дается в разделе 8.4.

После аппроксимации исходного объекта конечными элементами с должным количеством узлов каждому узлу сопоставляется неизвестная величина, которая ищется в процессе решения задачи. Например, для рис. 8.3, а неизвестными были бы смещения узлов по координатам х и у. Отсюда следует, что у каждого узла будет две степени свободы, а у задачи в целом будет 2п степеней свободы, если число узлов равно п. В разделе 8.2 мы покажем, что смещение в любой точке конечного элемента выводится из смещений его узлов при помощи функций формы, поэтому неизвестными могут быть только смещения узлов. Функции формы служат лишь для того, чтобы вычислять значения неизвестных внутри элемента по заданным значениям на его узлах2. После вычисления смещений программа может перейти к расчету деформаций как частных производных от функции смещения, а по деформациям рассчитываются напряжения.

Аппроксимировав область задачи набором дискретных конечных элементов, мы должны задать характеристики материала и граничные условия для каждого элемента. Указав различные характеристики для разных элементов, мы можем анализировать поведение объекта, состоящего из разных материалов. Граничные условия (смещение, внешняя сила или температура) обычно задаются на внешней границе объекта. Эти условия должны быть выражены в виде значений смещения, силы или температуры в граничных узлах некоторых конечных элементов. После задания граничных условий для всех внешних узлов программа конечноэлементного анализа формирует систему уравнений, связывающую граничные условия с неизвестными (смещениями или температурой в узлах или коэффициентами функции формы в /т-версии), после чего решает эту систему относительно неизвестных. Процесс формирования и решения системы уравнений рассматривается в разделе 8.2.

После нахождения значений неизвестных пользователь получает возможность рассчитать значение любого параметра в любой точке любого конечного элемента по той же функции формы, которая использовалась при построении системы уравнений. Выходные данные программы анализа методом конечных элементов обычно представляются в числовой форме. В задачах механики твердых тел выходными данными являются смещения и напряжения. В задачах на тепло-

1 Функции формы - независимые полиномы, определяющие аппроксимацию переменной, относительно которой решается задача.

В р-версии функция формы представляет собой полином высокого порядка, а коэффициенты этого полинома также считаются неизвестными, которые ищутся в процессе решения задачи.

перенос выходными данными являются температуры и тепловые потоки через конкретные.элементы. Однако по числовым данным пользователю бывает затруднительно получить общее представление о поведении соответствующих параметров. Графические изображения обычно более информативны, поскольку дают возможность изучить поведение параметров на всей области задачи. Анализ поведения параметров может производиться при помощи постпроцессора, который строит кривые и контурные графики переменных по данным программы конечноэлементного анализа. Для задач строительной механики возможно отображение деформированных тел вместе с недеформированными. В этой области для систем автоматизированного конструирования очень важными становятся функции компьютерной графики.

Мы завершим вводный раздел обсуждением ограничений метода конечных элементов. Многие конструкторы страдают чрезмерной верой в мощь этого метода, не имея представления о его ограничениях; они принимают неправильные результаты без тени сомнения. К преимуществам метода конечных элементов относится возможность работы с телами произвольной геометрии и неоднородными материалами. Однако суть метода состоит в делении области задачи на набор конечных элементов и поиске наилучшего решения, непрерывного внутри элементов, но имеющего возможность претерпевать скачки на их границах. Например, деформация на границе конечных элементов кронштейна (рис. 8.3, а), может испытывать скачок, невозможный с точки зрения физики. Величина такого скачка часто служит мерой точности решения, полученного методом конечных элементов. Неточности такого рода зависят от количества элементов, их размера и степени функции формы, используемой внутри каждого из элементов.

8.2. Формулировка метода конечных элементов

Как уже отмечалось, программы анализа методом конечных элементов формируют системы уравнений с неизвестными, учитывая заданные граничные условия. Затем система уравнений решается относительное неизвестных, а по найденным решениям рассчитываются значения характеристик внутри элементов. В этом разделе мы рассмотрим процедуру построения системы уравнений в классическом варианте метода конечных элементов (/г-версия). Чтобы вывести уравнения для задач строительной механики, мы воспользуемся принципом виртуальных перемещений. Мы будем следовать схеме именования переменных, принятой в работе [10], чтобы заинтересовавшийся читатель мог с легкостью найти в ней ответы на свои вопросы. Для вывода системы уравнений из основных дифференциальных уравнений используется иная процедура, описанная в приложении Л.

Рассмотрим трехмерный объект произвольной формы, находящийся в равновесном состоянии под воздействием некоторой нагрузки (рис. 8.4). Силы трения, действующие на поверхность, обозначим fs, массовые силы - fв, а сосредоточенные внешние силы - F. В общем случае эти силы раскладываются на компоненты, параллельные осям координат:

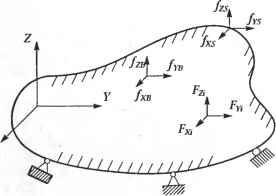Рис. 8.4. Трехмерный объект с внешними силами

Обозначим смещения произвольной точки объекта (X, Y, Z) по сравнению с конфигурацией в отсутствие нагрузки символом U. Тогда

UT = [U(X,Y,Z) V(X,Y,Z) W(X,Y,Z)], (8.2)

где индекс 1 означает транспонирование. Смещения U приведут к возникновению деформаций

ЕТ = [Ела- Еп- E/z У at Ууг Угх 1 (83)

и соответствующих напряжений

*T=Kva tit Tzz -Cat Trz Tzx ] С8-4)

Наша задача состоит в том, чтобы рассчитать U, е, т в точке (X, F, Z) по заданным внешним силам. Возможно, вы знакомы со следующим подходом к этой задаче: основные дифференциальные уравнения равновесия записываются путем наложения условия равновесия на элементы объекта, после чего эти уравнения решаются с учетом граничных условий и условий совместности.

Существует равноправный подход к описанию равновесия объекта - принцип виртуальных перемещений. Согласно этому принципу, равновесие объекта требует, чтобы для любых совместных малых виртуальных смещений, удовлетворяющих существенным граничным условиям, полная внутренняя виртуальная работа была равна полной внешней виртуальной работе. Отсюда уравнение равновесия может быть записано следующим образом:

JveTxdV =lJUT{BdV + \ps f5</S + £UV. (8.5)

Левая часть уравнения (8.5) описывает виртуальную внутреннюю работу, выполняемую реальными напряжениями на виртуальных деформациях, вызванных виртуальными смещениями U. В этом выражении

ёТ = 1ёХА- ё1т уХу yrz yzx ]. (8.6)

Слагаемые в правой части выражения (8.5) описывают внешнюю работу, выполняемую реальными силами fв, fs и F1 на виртуальных перемещениях U, где

UT = [U(X,Y,Z) V(X,Y,Z) Z(X,Y,Z)]. (8.7)

Верхний индекс 5 у вектора U означает виртуальное смещение на поверхности, а верхний индекс i - смещение в точке приложения сосредоточенных сил Р. Уравнение (8.5) включает также требования на совместимость и констнтутив-ность непрерывных функции смещений, которые удовлетворяют граничным условиям. Напряжения вычисляются через деформации по соответствующим материальным уравнениям. Поэтому принцип виртуальных перемещений включает все требования, которым должно удовлетворять решение задачи строительной механики.

Посмотрим теперь, как из уравнения (8.5) получаются уравнения метода конечных элементов. Начнем с аппроксимации объекта, изображенного на рис. 8.4, сеткой конечных элементов. Элементы соединяются друг с другом в узловых точках, которые находятся на их границах. Смещение в любой точке с координатами (х, у, z) в локальной системе координат элемента считается функцией смещений в узловых точках1. То есть для элемента т высказывается предположение, что

и < > (л-, у, z) = Н<га> (л-, у, 2)U, (8.8)

где Н(т) - интерполяционная матрица смещений, a U - вектор смещений на всех узлах. Если общее количество узлов равно N, вектор U запишется следующим образом:

ит=[и, , w, u2 v2 w2 ... Ыд. vN wN\. (8.9)

Это выражение можно переписать так:

ит=[£Д иг и3 - Л (81°)

где Ut может задавать смещение в любом направлении, а п соответствует общему количеству степеней свободы. Далее мы будем использовать это выражение для U.

Хотя в уравнении (8.10) перечисляются смещения всех узлов, а следовательно, эти смещения входят и в выражение (8.8), для каждого конкретного элемента смещения внутри него определяются только смещениями в его собственных узлах. В уравнение же (8.8) все узлы вошли потому, что это облегчает процесс объединения матриц отдельных элементов в матрицу структуры в целом, как будет показано ниже.

Уравнение (8.8) позволяет вычислить деформации:

E\x,y,z)=Blm\x,y,z)XJ. (8.11)

Строки матрицы деформаций-смещений В(и) из уравнения (8.11) получаются дифференцированием и объединением строк матрицы Н(т). Производные матриц Н( ° и В' 0 рассматриваются в примере 8.1.

1 В р-версии смещение включает две составляющие. Первая определяется смещениями узлов, как и в (8.8), зато вторая описывает иерархическое смещение, выражаемое полиномом произвольной степени. Подробнее ор-версин конечпоэлементного анализа можно прочитать в работах [103, 148].

Теперь мы можем записать и выражения для напряжении внутри каждого элемента:

т

( ) =С( )е( ) +х'(га>, (8.12)

гдеС(т> - матрица упругости элемента тп, а т/<га) - начальное напряжение внутри элемента. Матрица упругости, которая связывает напряжения с деформациями, подробно изучается в учебниках по основам сопротивления материалов [26]. В структуре, состоящей из разных материалов, для каждого элемента можно задать свою собственную матрицу упругости. Кроме того, матрица упругости позволяет учесть изотропию или анизотропию свойств материала.

Перед тем как подставить выражения (8.8), (8.11) и (8.12) в формулу принципа виртуальных смещений, мы перепишем уравнение (8.5) в виде суммы интегралов по объемам и поверхностям отдельных элементов:

ZL*e(m)V -W(ra> =£rwu< >TfB< >dv< > +

(8.13)

+ ZLwu5(m)Tf5< M5<ra>+XUTF,

т . i

где т изменяется от 1 до полного количества элементов в системе.

Подставляя выражения (8.8), (8.11) и (8.12) в (8.13), будем предполагать, что виртуальные смещения в элементе U<m> связаны с виртуальными узловыми смещениями U той же матрицей Н(га) из (8.8). Эта подстановка даст следующее выражение:

I + {zi н5(га)Т f5( w->} - jz в< >т x<: w>} + f

(8.14)

где поверхностные интерполяционные матрицы смещений Н5(га) получаются из объемных интерполяционных матриц смещений Н(га> подстановкой координат поверхности элемента. F - вектор внешних сосредоточенных сил, действующих на узловые точки. Компоненты вектора F соответствуют компонентам смещений вектора U. Обратите внимание, что в уравнении (8.14) вектор U вынесен за знак суммирования, потому что он не зависит от рассматриваемого элемента.

Чтобы выражение (8.14) было верным для произвольного виртуального смещения (а это и есть условие равновесия), должно выполняться следующее равенство:

ZJywBC 8 U = XtwH( )rfB( )( ) +

- m J га (8.15)

+ZJ5H5(m)Tf5(raW > -UrtBxW +F.

tn m

Будем отныне обозначать смещения в узлах просто буквой U. Перепишем уравнение (8.15) в виде

KU=R, (8.16)

где

Обратите внимание, что суммирование интегралов по объемам отдельных элементов в формуле (8.17) выражает тот факт, что матрица жесткости набора элементов как целого получается сложением матриц жесткости элементов К<га). Аналогичным образом, вектор RB объемной силы, действующей на все тело, получается суммированием векторов объемных сил, действующих на отдельные Элементы. Тем же путем вычисляются и векторы прочих сил.

Выражение (8.16) описывает статическое равновесие. Если приложенные силы изменяются во времени, это выражение применимо к любому конкретному моменту. Однако при быстром приложении нагрузки необходимо учитывать силы инерции. По принципу Даламбера силы инерции отдельных элементов могут быть добавлены к массовым силам. Если предположить, что ускорение в любой точке элемента связано с ускорениями в узловых точках матрицей Н(га) подобно смещениям, вклад массовых сил в вектор нагрузки R будет выражаться так:

rb = ZtwH< ,T [fB( } -p<ra)H< )U]( >, (8.23)

где U - ускорения узловых точек, а р(га) - массовая плотность элемента тп. Слагаемое fВ(га) в выражении (8.23) больше не включает никаких сил инерции.

Подстановка (8.23) вместо (8.19) в (8.15) дает новое уравнение равновесия:

MU + KU=R, (8.24)

Жде М - матрица масс, определяемая следующим образом:

м = Z 1 Р< >Н<га)ТН(и)( ). (8.25)

Обратите внимание, что U и R в уравнении (8.24) являются функциями времени.

Демпфирующие силы могут быть учтены как дополнительный вклад в массовые силы, что позволяет описать эффект демпфирования (затухания). Уравнение (8.23) при этом принимает новый вид

rb =Zfv H( )T[fB< ) -p( )H( )0-K< )H( )tT]dV( ,), (8.26)

где U - вектор скоростей узловых точек, а к' 0 - демпфирующий коэффициент для элемента тп.

Уравнение равновесия приобретает вид

MU + CU + KU = R, (8.27)

где С - матрица демпфирования, структура которой описывается выражением

с = Е[,<- > к^Н* 1 H(m)dT<т) (8.28)

На практике матрицу С обычно конструируют из массовой матрицы и матрицы жесткости на основании экспериментальных данных по демпфированию в материале, потому что определить параметры демпфирования отдельных элементов достаточно сложно.

Приведенный ниже пример иллюстрирует изложенную процедуру вывода системных уравнений.

Пример 8.1

Вывести и решить системные уравнения для пластины, нагруженной так, как показано на рис. 8.5, с, используя двухэлементную модель (рис. 8.5, б). Модуль Юнга и коэффициент Пуассона материала, из которого изготовлена пластина, равны Е и v соответственно. Толщина пластины постоянна и равна 1 см. Считайте, что нагрузка Ру прикладывается постепенно, благодаря чему силами инерции можно пренебречь.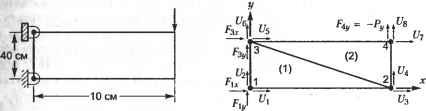

а б

Рис. 8.5. Анализируемая структура

Решение

На первом этапе необходимо построить векторы Н(га) и В(га) для т = 1, 2, соответствующие смещениям U1 = [U, U2 U3 UA U5 U6 U1 U8 ]. Чтобы вывести матрицу H(,) произвольного элемента, следует рассмотреть треугольный элемент (рис. 8.6). Смещения внутри треугольного элемента с тремя узлами могут считаться линейными. Следовательно, выражения для смещений внутри каждого элемента в направлениях х иу будут иметь следующий вид1:

и = а, + а2х + а3у; (8.29)

=Р, + р2* + р3у. (8.30)

Мы можем по той же формуле выразить смещение каждого из узлов:

и, =сц +а2х, + а3у а, =р, + В2-Г, + Р3# и2 =а, +a.2x2 + а3у2, v2 =р, + p2x2 + $3у2; и3 =а, +а2х3 + а3у3, v3 = Р, + $2х3 + Р3#3.

1 Функции а, + а2х + а3у и + Р2х + $3у играют роль интерполяционных функций.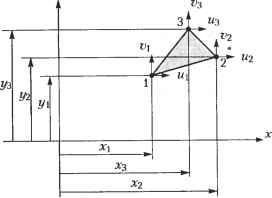

Рис. 8.6. Треугольный элемент с тремя узлами

Одновременное решение этих уравнений позволяет определить константы а, р через щ, Xj, у,. Таким образом получаются следующие выражения для а р, :

2 =

Р, Р2 Рз

где

а, =х2у3 ~х3у2, Ь, =у2 -у3,с, =х3 -х2\ а2 = x3yi -х{у3, Ъ2 =у3 -у с2 =х, -.г.,;

°3 =Х1У2 ~Х2У\ Ь3 =у, ~У2,сз = Х2 ~хг

2а = а1 + а2+ а3.

Подстановка значений х х2, хл, уь у2, у3 для элемента 1 в эти уравнения дает

После того, как выражения для а, и Р, будут подставлены обратно в уравнения (8.29) и (8.30). смещения и и v можно будет записать в форме и = В,[х,у)щ + В2(х,у)и2 + +В3(х,у)и3, v = Д(х,y)v, + B2(x,y)v2 + B3(x,y)v3. Функции В,(х, у), В2(х, у) и В3(х, у) называются функциями формы.

и = и. +--и. + -Un \х + \ -и. + -и, у;

1 I 10 1 10 2) { 4 1 4 л)у

( 1 \ \ ( \ \ \

V = v, +\--V. +-v7 \х + \--V. + -V у.

1 Л 10 1 10 2) { 4 1 4 3)

(8.31)

Уравнение (8.31) можно переписать в матричной форме:

1--х--у

10 4

-х 0 -у 0 О О 10 4

О -х О 10

У о О

и* и? и

(8.32)

Аналогичным образом получается выражение для смещений в элементе с номером 2:

0 И) 0 N) hH

(8.33)

На следующем шаге определяются деформации, то есть матрица В(га). Для этого мы воспользуемся соотношениями между смещениями и деформациями для двумерного случая:

ди dv 3 5ы

дх ду

Таким способом из выражений (8.32) и (8.33) получаются функции Е°\х,у,г), £l2)(x<y,zy.

Е<> =

0 0 0 0 0

-- О -

10 10

0 - 0 00-00 4 4

11 11

-± L о - - 0 0 0

4 10 10 4

и, и, и,

= B( U; (8.34)

Е(2) =

о -- 10

-- о

0 -

о о

о

A J 4 10

= B(2)U. (8.35)

Соотношение между деформациями и напряжениями для однородной изотропной пластины выглядит так:

т(и) =

1 V V 1

-(l-v)

(8.36)

Предполагается, что изначально структура не была напряжена.

Матрица жесткости для каждого элемента получается подстановкой результатов (8.34)-(8.36) в уравнение (8.17). Рассматриваемые элементы сделаны из одинакового материала, поэтому выражение дляС<т) из (8.36) может использоваться для них обоих. (В приведенном ниже выводе интеграл по объему преобразуется к интегралу по поверхности благодаря тому, что пластина имеет единичную толщину.)

К() =И1)В(,)ГС(1>В(,)(1) =£(1,В(,)ГС(,)В(1><£4() =

= £°В()ГС()В(4-

-х

dx =

l-v2

-- 0 - 0 0 0 0 0

10 10

О -1 о 00-00

Л J о --ооо

4 10 10 4

о

-- о

i -J- 0 - -

4 10 10 4

0 0 0 0 0

0 0 0

0 0

[ 4--х I dx

20Е 1-v2

Г 1 , 1-v

100 + 32 1 + p

80 1

1-е

80 1-p

~40 0

1 + v

80 1 н 1-p

16 + 200

~~40 1-v

200 1-p

40 1

100 0

40 0

1-v 1-v

80 1-v

200 1-v

32 1-p

80 l-v

40 J

40 0

J 16

о 0 о 0

к<2> = /ияв<2>гс<2>в<2>ат<2> =

1-v2

0 1-v

80 1-v

32 1-v

l(2)B(2fC<2W2>dA<2> =

0 0 0

40 0

40 Jl

40 1

v

0 1-v

200 1-p

l-.v

32 v

40 1

100 1-p

80 1 1-

100 + 32 1 + p

i 16

40 1-p

200 1 + p

~W -1 lz

16 200

(8.38)

wI(S)T(838T СТРУКТУРЫ KaK целого случается объединением уравне-

20Е

1

~40 1 1-р

100+ 32

о

1+р

80 1-е

32 1-р

80 1-р

200

J. iz£

16 + 200 1+г

О

40 1(1

1-р

1-й 80 О 1+р

1 1-р

100+ 32 О

1

р

40 1

К> 1 +р

О

1-в 200

80 1-р

р

40 1

1 1-й

100 32 1+г

80 1

г

200 1+р

1-р ] 200

(8.39)

Вектор нагрузки R совпадает с вектором R потому что на узлы действуют только сосредоточенные силы. Отсюда

о

(8.40)

где Ру - известная внешняя сила, a Flv, г7 F3v и F3l/ - неизвестные силы реакции опоры.

Теперь нужно найти неизвестные смещения узловых точек из приведенного ниже уравнения:

k-,a

(8.41)

где элементы матрицы жесткости из уравнения (8.39) обозначены k,r

Вы можете самостоятельно убедиться и том, что матрица жесткости в уравне нии (8.39) вырожденна, а потому уравнение (8.41) решить невозможно. Аналогичная ситуация возникает при решении дифференциальных уравнений, которые не дают единственного решения без граничных условий. Так, решение (8.41) можно получить, если учесть в этом уравнении граничные условия:

kn kn kt3

k2i k22 k23

k7l k12 kJ3 ksl kg2 ks3

k21 klg kg7 88

(8.42)

Уравнение (8.42) может быть разделено на два независимых матричных уравнения:

(8.43)

(8.44)

Мы можем решить уравнение (8.43) относительно неизвестных узловых смещений U3, Щ, U- U8 и подставить найденные значения в уравнение (8.44), после чего определить неизвестные силы реакции опоры Fly, F3x и F3y. Большая часть программ, реализующих метод конечных элементов, действует именно в этой последовательности.

Определив смещения узлов, мы можем рассчитать деформации и напряжения в элементах по приведенным выше уравнениям. Отсюда мы можем сделать вывод, что смещения играют достаточно важную роль в анализе структуры. Это одна из причин, по которым формулировка метода конечных элементов, предложенная в этом разделе, считается основанной на смещениях (displacement-based formulation).

8.3. Моделирование конечных элементов

Анализ методом конечных элементов является мощнейшей технологией, позволяющей моделировать распределение напряжений, температур, потоки жидкостей и распространение электромагнитных полей, однако до сих пор нерешенной остается проблема подготовки данных для проведения анализа: выбор геометрии, построение сетки конечных элементов, добавление граничных условий и нагрузок, задание свойств материалов и выбор типа анализа (статический или динамический, линейный или нелинейный, анализ деформаций, напряже-

ний и т. д.). Действия, относящиеся к подготовке данных, обобщенно называют моделированием конечных элементов (finite-element modeling). Выполняются эти действия чаще всего препроцессором, рассчитанным на работу с какой-либо конкретной программой анализа методом конечных элементов (finite-element analysis - FEA).

Работа с препроцессором начинается с выбора геометрии объекта или области задачи. Традиционные системы FEA обладают лишь зачатками функций моделирования конечных элементов, тогда как большинство современных систем либо снабжаются расширенными средствами моделирования, либо позволяют обмениваться данными с системами геометрического моделирования (а иногда предлагают пользователю и то, и другое вместе) [117]. Системы, рассчитанные на подготовку геометрической модели в системах автоматизированной подготовки чертежей, либо работают непосредственно с данными CAD, либо преобразуют и импортируют их. Вариант поверх CAD (direct on CAD) становится в последнее время все более популярным, поскольку он устраняет преобразования (которые могут повлечь потерю данных) и сокращает длительность цикла проектирование - анализ - изменение . Более того, использование CAD упрощает моделирование и дает возможность работать с более сложными функциями создания и изменения геометрических форм. Современные гибридные системы моделирования (интегрирующие объемное, поверхностное и каркасное моделирование1 с параметрическим и объектно-ориентированным подходами) позволяют создать практически любую нужную для анализа геометрию. Большинство систем FEA могут также импортировать геометрические данные либо через промежуточные файлы стандартных форматов (типа IGES2), либо непосредственно из конкретных CAD. Однако использование геометрических моделей, подготовленных в CAD, не всегда оказывается простым делом. Модель, которую конструктор сочтет идеальной, может на самом деле содержать недопустимые в FEA элементы. Особенно это касается построения сеток. Некоторые системы уже предлагают функции проверки импортированных моделей. Более того, даже если построенная в CAD модель свободна от недостатков, она может быть чересчур подробной. Например, такие характерные детали, как фаски, в некоторых случаях вполне могут быть исключены из модели для анализа методом конечных элементов. Подобные решения принимаются конструктором исходя из ожидаемого размера ячеек сетки, а также из интуитивных предположений о важности отдельных участков объекта. Некоторые программы обладают функциями удаления элементов (defeaturing), то есть временного скрытия деталей, не влияющих на точность анализа. Абстрагирование является основной причиной различий между моделями одного и того же объекта, используемыми проектировщиками и аналитиками. Изменения, предлагаемые одними из них, не могут непосредственно воплощаться в модели других. В настоящее время ведутся исследования возможности автоматического абстрагирования объемных моделей [3].

1 Немногообразиые системы моделирования поддерживают интеграцию объемных, поверхностных и каркасных моделей в наиболее общем виде.

2 Описан в главе 14.

Следующий шаг - создание ячеек сетки и распределение узлов. Когда каждой ячейке сопоставляются узлы, она становится конечным элементом. Построение сетки является важнейшим и сложнейшим этапом моделирования. Для упрощения этой задачи практически все системы на сегодняшний день предлагают те или иные функции автоматизации. Наиболее типично использование тетраэдри-ческих элементов для объемных тел и четырехугольных или треугольных элементов для трехмерных поверхностей, оболочек и двухмерных объектов. Многие системы предоставляют пользователям возможность изменять параметры автоматически формируемых сеток, в частности плотность ячеек. Кроме того, в таких системах обычно имеются функции ручного локального редактирования, позволяющие уточнить сетку в критических областях. Многие системы связывают сетку с геометрической моделью, так что изменение последней автоматически влечет за собой изменение первой.

От сложности сетки зависит размер глобальной матрицы жесткости, численная сложность задачи и объем требуемых вычислительных ресурсов. Точность решения можно повысить увеличением количества ячеек или использованием функций формы более высоких порядков. Конечные элементы должны удовлетворять определенным требованиям. Во-первых, размерность элементов должна совпадать с размерностью области задачи. Для одномерных задач используются одномерные элементы, для двумерных - двумерные, и т. д. Во-вторых, конечные элементы должны поддерживаться выбранной программой FEA. Другими словами, программа должна уметь рассчитывать вклад конкретного элемента в матрицу жесткости. Все элементы, поддерживаемые пакетом анализа, составляют его библиотеку (element library). Чем больше элементов в библиотеке, тем большее число задач может решать программа. Наиболее типичные конечные элементы, поддерживаемые большинством программ анализа, демонстрирует рис. 8.7. Обратите внимание, что одна и та же ячейка может становиться элементами разных типов в зависимости от количества узлов на ее границах. Наконец, в зонах, где ожидаются резкие изменения неизвестных (напряжения, например, сосредоточиваются в окрестностях отверстий), плотность узлов и ячеек должна быть выше, чем в областях с плавным изменением параметров.

Другой подход к решению проблем формирования сетки предлагает р-версия конечноэлементного анализа. Р-версия использует простые сетки, формируемые автоматическими методами, но зато в этой версии может изменяться степень функции формы (также автоматически). Существует достаточно много программ FEA, поддерживающих р-версию анализа, но только две программы были разработаны специально для этой версии: Pro/MECHANICA фирмы РТС и PolyFEM фирмы CADSI. Преимущества этого подхода не ограничиваются простотой сеток. Р-версия позволяет задавать конкретные ограничения на точность, а также лучше аппроксимировать геометрические модели из программ CAD. Низкий уровень точности позволяет конструктору быстро получить результаты анализа на предварительном этапе разработки.

За выбором элементов следует задание типа анализа (статический или динамический, линейный или нелинейный, анализ деформаций, напряжений и т. д., как уже отмечалось). С каждым узлом связываются неизвестные или степени свободы. К неизвестным относятся смещения, повороты, температура, тепловые пото-

ки и т. п. Затем задаются граничные условия. Для непрерывных границ объекта известными могут быть смещения, внешние силы и температура. Эти сведения должны быть выражены в виде значений соответствующих параметров в кон кретных граничных узлах. Иногда требуется формирование конечных элементов без граничных условий. Если необходимо учесть точечные воздействия, в соответствующих точках должны располагаться узлы. Большинство систем анализа, интегрированных с CAD, дают пользователю возможность задавать граничные условия непосредственно на геометрической, модели, после чего эти граничные условия преобразуются к эквивалентным условиям на узлах системы. Нагрузки и граничные условия задаются множеством способов, что позволяет решать задачи самого широкого круга и моделировать реальные условия достаточно точно.

Элементы типа балки и фермы

2 узла (линейный) 3 узла (квадратичный) 4 узла

(кубический)

Треугольные элементы

Квадратные элементы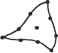

3 узла 6 узлов (квадратичный) 10 узлов (кубический) (линейный) .

су а а

4 узла (линейный) 8 узлов 12 узлов (кубический)

(квадратичный)

Тетраэдальные элементы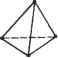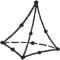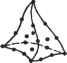

4 узла (линейный) 10 узлов 20 узлов (кубический) (квадратичный)

Призматические элементы

7 узлов (линейный) 16 узлов 29 узлов (кубический) (квадратичный)

Гексаэдрапьные элементы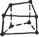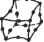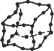

8 узлов (линейный) 20 узлов 32 узла (кубический) (квадратичный)

Рис. 8.7. Типы конечных элементов разных размерностей

Для каждого элемента обязательно задание свойств материала. Обычно эти параметры включают модуль Юнга и коэффициент Пуассона (для задач строительной механики). Толщина оболочек и пластин рассматривается скорее как свойство материала, чем как геометрический параметр, что позволяет избежать перехода к трем измерениям. Для задач других типов могут быть заданы теплоемкость или вязкость. Разные элементы могут иметь разные свойства, благодаря чему пользователь может анализировать составной объект, о чем уже говорилось выше. Основные сложности в описании составных объектов возникают при задании интерфейсов.

Полностью определенная конечноэлементная модель со всеми параметрами передается программе анализа. Решенная задача подготавливается к исследованию постпроцессором. Большинство пакетов позволяют вычислять различные параметры, выводить их в виде таблиц или графиков. Чаще всего требуется вывод данных о деформациях, напряжениях и изменении формы. Для этой цели традиционно используются контурные графики, на которых распределение параметров кодируется различными цветами непосредственно на изображении объекта. Большинство пакетов уже ушли довольно далеко от столь примитивной графики. Пользователь современной системы может выводить на экран изоповерхно-сти (поверхности с постоянными значениями какого-либо параметра) или поперечные сечения. Для динамического анализа удобно наличие средств анимации, позволяющих проводить нелинейный анализ временной эволюции систем. Все более возрастает потребность в выводе графиков и роликов в форматах, пригодных для использования в других программах, документах, презентациях и Сети.

8.4. Автоматическое построение сетки

Построение сетки подразумевает определение положения узлов и элементов, а также автоматическую нумерацию узлов и элементов с минимальным объемом вводимых пользователем данных. Предполагается, что методы полностью автоматического формирования сетки (fully automatic mesh generation) требуют только задания геометрической модели (геометрии и топологии) объекта, подлежащего разбиению на элементы, свойств сетки, таких как плотность ячеек и типы элементов, а также граничных условий, включающих внешние нагрузки. Методы, не входящие в эту категорию, могут требовать ввода дополнительных данных, в частности разбиения объекта на несколько частей. Такие методы считаются полуавтоматическими. В этом разделе мы кратко расскажем о методах формирования сеток, используя схему их классификации, предложенную Хо-Ли [70]. В отдельных местах мы будем воспроизводить его дословно и приводить иллюстрации без изменений.

8.4.1. Соединение узлов

Чрезвычайно популярный подход к проблеме построения сетки состоит в соединении узлов. Популярность этого подхода объясняется простотой его концепции. Метод делится на две основные фазы: создание узлов (рис. 8.8, а) и построение элементов (рис. 8.8, 6).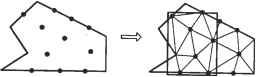

Рис. 8.8. Соединение узлов

Создание узлов

В опубликованных работах, посвященных задаче создания узлов, можно найти следующие методы.

□ Метод Кавендиша [29]. По этому методу работа начинается с задания граничных узлов вручную. Затем программа осуществляет автоматическое создание внутренних узлов с учетом требований к плотности ячеек. Объект делится на участки, размер которых соответствует размеру элементов. В участке i создается квадратная сетка масштаба r(i). Одиночная сетка, построенная в предположении, что плотность конечной сетки должна быть постоянной, изображена на рис. 8.9. В каждом квадрате сетки случайным образом создается один внутренний узел. Это может быть реализовано выбором двух случайных чисел от 0 до 1 и расчетом координат точки по соответствующим осям квадратной ячейки. Если узел попадает внутрь объекта, а расстояние от него до граничных и автоматически созданных на предыдущих шагах алгоритма узлов оказывается большим r(i), этот узел считается принятым. В противном случае случайным образом выбирается следующий узел, который проходит ту же проверку. Если за фиксированное количество попыток (например, пять) принять узел не удается, квадратная ячейка сетки просто пропускается, и программа переходит к следующей ячейке. Этот метод может быть расширен до трех измерений простым переходом от плоской квадратной сетки к пространственной кубической.

Рис. 8.9. Создание узлов по методу Кавендиша

□ Метод Шимады [141]. Этот метод требует представления внутренней области объекта заполненной пузырьками (рис. 8.10). Центральные точки пузырьков становятся узлами. Размер пузырька определяется температурным распределением, соответствующим заданной плотности сетки. Положения пузырьков определяются условиями равновесия с учетом всех сил реакции, действующих между ними.

Рис. 8.10. Создание узлов методом Шимады

Построение элементов

На этом этапе осуществляется соединение узлов, в результате чего получаются элементы, которые не должны перекрываться, но должны покрывать всю площадь объекта. Мы рассмотрим метод Ли, который может давать четырехугольные элементы. Однако наиболее популярным методом соединения узлов является метод триангуляции Делоне. В нижеследующем рассмотрении мы будем учитывать только те элементы, у которых узлы находятся в вершинах. Если задача требует использования элементов с промежуточными узлами, их легко можно построить по элементам с узлами в вершинах. Поэтому мы не будем исследовать промежуточные узлы во всех описываемых ниже методах.

□ Метод Ли [98]. Согласно этому методу, на объект накладывается квадратная сетка, размер ячеек которой соответствует ожидаемому размеру элементов. Затем узлы, полученные на предыдущем этапе, связываются с ячейками этой сетки. Ячейки и соответствующие им узлы перебираются по столбцам слева направо и сверху вниз. Внутри ячейки узлы упорядочиваются по возрастанию абсцисс. Узлы с одинаковыми абсциссами сортируются по возрастанию ординат. Узлы перебираются последовательно, причем из соседних узлов выбираются такие, с которыми данный узел образует хороший четырехугольник. Если же четырехугольник оказывается плохим , вместо него формируется треугольник.

□ Триангуляция Делоне [155]. Это, пожалуй, наиболее популярный метод формирования треугольников путем соединения узлов, поскольку он максимизирует сумму наименьших углов во всех формируемых треугольниках. Иначе говоря, данный метод триангуляции ориентирован на то, чтобы по возможности избегать формирования узких треугольников.

Триангуляция Делоне обычно начинается с диаграммы Вороного или полигонов Дирихле [57]. Диаграмма Вороного (Voronoi diagram) множества N точек P,(i=l,

2.....N) состоит из N многоугольников (многогранников, если задача решается в

трех измерениях) Vit центры которых находятся в точках Р„ причем многоугольники эти представляют собой геометрическое место точек, для которых данный узел i является ближайшим. Математическая запись этого утверждения относительно многоугольника Vt выглядит следующим образом:

V, ={ж|х-р\ <х-р, V/*i}. (8.45)

Многоугольник (многогранник) Vt является выпуклым. Он ограничивается прямыми (плоскостями), проходящими через середины отрезков, соединяющих

узел Pt с его соседями, и перпендикулярными этим отрезкам. Такое разбиение двумерного или трехмерного -пространства называется полигонами Дирихле (Dirichlet tesselatiori). Каждый многоугольник (многогранник) Вороного связан с одним определенным узлом. Построив диаграмму Вороного, мы можем перейти к созданию треугольных (тетраэдрических) элементов, соединяя точки соседних многоугольников (многогранников) Вороного. Диаграмму Вороного и результат триангуляции для десяти узлов на плоскости демонстрирует рис. 8.11.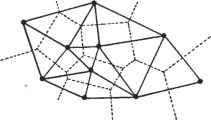

Рис. 8.11. Диаграмма Вороного и триангуляция Делоне

Триангуляция Делоне может производиться непосредственно на наборе точек (узлов) с использованием алгоритма двухмерной триангуляции Ватсона [155] без предварительного построения диаграммы Вороного. Согласно этому алгоритму, три точки, не лежащие на одной прямой, объединяются в треугольник, если окружность, проведенная через эти точки (описанная окружность для будущего треугольника), не захватывает никаких других точек. Алгоритм реализуется следующим образом. Сначала строится треугольник Т0, внутри которого находятся все узлы. Вершинами этого треугольника могут быть и точки, не являющиеся узлами. Затем осуществляется перебор узлов из полного их множества, и для каждого узла ищутся треугольники, такие, что описанная вокруг них окружность захватывает данный узел. Эти треугольники (называемые пересеченными) в дальнейшем не рассматриваются. На рис. 8.12, б они обозначены знаком X. Затем вместо них строятся новые треугольники, образуемые соединением добавленного узла с вершинами пересеченных треугольников (рис. 8.12, в).

Рис. 8.12. Алгоритм триангуляции Ватсона

На заключительном этапе удаляются треугольники, полученные соединением узлов с дополнительными точками, введенными на первом этапе для построения треугольника Т0. Эта процедура легко обобщается на трехмерное пространство путем перехода к использованию описанных сфер для четырех узлов вместо