делают поверхность более плоской, F-лоскут не может использоваться для моделирования поверхностей с большой кривизной. Однако он хорошо описывает поверхности с нулевой кривизной по крайней мере в одном направлении во всех точках.

Покажем теперь, как векторы кручения влияют на форму внутренней области поверхности. Если мы сможем показать, что векторы кручения определяют форму изопараметрической кривой v = v0 на рис. 7.3, мы сможем утверждать, что эти векторы влияют на любую внутреннюю изопараметрическую кривую, а значит, и на всю внутреннюю область лоскута. Точки А и В определяются граничными кривыми - эрмитовыми кривыми, которые не зависят от векторов кручения. Следовательно, мы должны показать, что векторы касательных в точках А и В определяются векторами кручения. Сделаем это, продифференцировав уравнение (7.18) по параметру и: dP(u,v)

du I

dFx(u) dF2(u) dF3(u) dF4(u) du du du du

p(o,o) P(o,i) рц(о,о) рдодЛГад

P(1,0) P(l,l) P.(1,0) PK(U) F2(v)

P (0.0) P (1,0) Pw(0,0) P (0,1) F3(v)

p.(i,o) pB<i,i) p№(i,o) pBB(U)Iw

= [-6ы + 6ы2 6ы-6ы2 l-4u + 3w2 -2m + 3w2]

G,(p) C2(v) G3(v) Gt{v)

(7.20)

Обратите внимание, что произведение второй и третьей матриц мы записали в виде вектора-столбца с элементами G[(o), G2(a), G3(v), GA(v). Чтобы вычислить производную по и в точке А, мы должны подставить в уравнение (7.20) значения ы = 0, v = % Подстановка и = 0 в вектор-строку делает ее равной [0 01 0], благодаря чему получается, что Р„(Л) = G3(v0 ). Поскольку G3(v0) определяется векторами Pu(0,0), Ри(0,1), Р„Д0,0) и Рир(0,1), мы заключаем, что векторы кручения Р„,(0,0) и Рар(0,1) определяют Ри(А).

Подставим и = 1, v = v0 в уравнение (7.20), чтобы выяснить, от чего зависит Ри(В):

Рц(В) = [0 0 0 1]

G2(v0) G3(v0) G4(v0)

= G4(o0) = [P (l,0) Рц(1,1) РНГ1(1,0) P (l,l)]

F2(v0) F3(z>0) \FA4,).

(7.21)

Мы показали, что вектор касательной в точке В зависит от векторов кручения Рив(1,0) и Рн[,(1,1). Отсюда мы делаем вывод, что векторы кручения влияют на любую внутреннюю изопараметрическую кривую, а следовательно, определяют форму бикубического лоскута.

7.5. Поверхность Безье

Можно расширить концепцию кривой Безье, определяемой задающим многоугольником, на одно измерение, в результате чего получится поверхность Безье. определяемая задающим многогранником. Уравнение поверхности Безье выглядит следующим образом:

п т

Р( .*>) = £ £Р„ Д, (u)Bjjn (v) (0 < и < 1.0 < v < 1), (7.22)

i-О у=о

где Р,v - радиус-векторы задающих точек, находящихся в вершинах задающего многогранника (рис. 7.4), а Bin и BJm - функции сопряжения, обычные для кривых Безье. Таким образом, степень уравнения поверхности nouuv определяется количеством задающих точек в соответствующих направлениях.

Уравнение (7.22) можно раскрыть, записав сумму по/ в явном виде:

P(u,v) = £[PiSJB0m(v) + PiABim(v)+... +Pi Ba (v)]Bij,(u). (7.23)

Уравнение (7.23) иллюстрирует, что поверхность Безье получается сопряжением п + 1 кривых Безье, каждая из которых определяется задающими точками Р, 0, Р ,1 > Р/.2 > > сопрягаемыми функциями Д, (ы). Можно показать, что та же поверхность Безье получается при сопряжении т + 1 кривых Безье, определяемых задающими точками P0j, Р1;, Р2......PnJ и функциями B)jn(v). Итак, поверхность Безье получается, если задающие точки кривой Безье заменить кривыми Безье.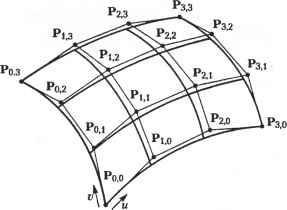

Рис. 7.4. Поверхность Безье с задающим многогранником

Займемся исследованием свойств поверхности Безье. Сначала нужно показать, что четыре угловые задающие точки задающего многогранника лежат на по-

верхности Безье. Для этого мы подставим граничные значения параметров ии v в уравнение (7.22). Подстановка м = Оии*0 дает:

р(о,о) = £ £р,Ал(0)я и(0) = £

1=0 j=0

1РуД>л(0)

л

= Х

Р,.оД. (0):

ХР..о

,.я(0) =

Jb=0

ы'О-ы)

Д. (0) =

(7.24)

Равенство (7.24) показывает, что задающая точка Р00 лежит на поверхности и юответствует значениям параметра и = 0, v = 0. Та же процедура позволяет проверить, лежат ли остальные угловые задающие точки (Ри0, Ро,га> Ри.т) на поверх-гости.

В дополнение к этому мы можем показать, что граничные кривые поверхности Безье также являются кривыми Безье, определяемыми соответствующим коли-1еством задающих точек. Подставим и = 0 в уравнение (7.22), чтобы получить равнение одной из граничных кривых.

Р(0,е) = X £РУ В, (0)В,. (v) = X

1=0 ;=0 j-0

£р„ . (1-й)

(7.25)

= Хро.А> -

у=о

Сравнение (7.25) говорит нам о том, что граничная кривая, соответствующая начению параметра и = 0, является кривой Безье с задающими точками Р00, *о 1, -, Ро,и- Аналогичным образом можно показать, что оставшиеся три граничив кривые также являются кривыми Безье, а их задающие точки являются райними вершинами задающего многогранника. Поскольку вектор касательной ia конце кривой Безье определяется соседней с концом задающей точкой, векто-ы касательных в направлении v в точках Р0,о и Р0т определяют точки Р01

Pon-i соответственно. Следовательно, P0,i и P0,ra-i играют ту же роль, что и (0,0) и Р„(0,1) для бикубического лоскута. Если с этой точки зрения подойти

поверхности Безье степени 3 по и и v (см. рис. 7.4), можно сделать следующее тверждение. Задающая точка Pi,0 играет ту же роль, что и Ри (0,0) для бикубиче-кого лоскута, Р2>0 - ту же, что Р„(1,0), Р, 3 - ту же, что Ри(0,1), Р23 - ту же, что (1,1), Р01 - ту же, что Р„(0,0), Р0,2 - ту же, что Рв(0,1), Р3>1 - ту же, что Р„(1,0), з,2 - ту же, что Рр(1,1). Следовательно, эти восемь задающих точек вместе с че-ырьмя угловыми задающими точками определяют граничные кривые поверхно-ги. Оставшиеся четыре задающие точки Р, Р21, Р, 2, Р2,2 определяют форму нутренней области поверхности подобно векторам кручения бикубического эскута.

1ы уже отмечали, что степень поверхности Безье определяется количеством за-дащих точек. Уравнения поверхностей высоких степеней страдают теми же не-

достатками, что и уравнения кривых высоких степеней, поэтому при моделировании поверхностей обычно используются поверхности Безье степени 3 по и и р, точно так же как при моделировании кривых использовались кривые Безье степени 3. При необходимости смоделировать сложную поверхность приходится создавать несколько поверхностей Безье третьей степени и соединять их друг с другом. Поверхности должны соединяться таким образом, чтобы обеспечивалась непрерывность на границе, по которой осуществляется соединение. Это достигается наложением ограничений на задающие точки, расположенные слева и справа от границы. Ограничение состоит в том, что эти точки должны лежать на прямой линии, проходящей через задающею точку, лежащую на общей границе (рис. 7.5). Если это требование выполняется, первая производная оказывается непрерывной во всех точках границы [72, 138, 46].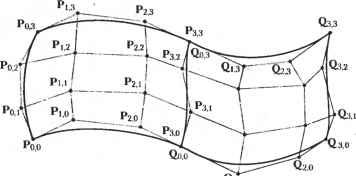

Рис. 7.5. Объединение лоскутов Безье

7.5.1. Вычисление поверхности Безье

Координаты х, у и z точки поверхности Безье, соответствующей значениям параметров и = щ и v = v0, вычисляются по формуле:

Р( о.О = 1ХР Ая( о)В/,>о)-

;=о j=0

Перепишем уравнение (7.26), раскрыв сумму по i:

(7.26)

рк-о) = X Хр,.А>о Щ.Л 0) =

1=0 >=0

Хро.А.,>о)

;=о

В0.>о) +

Хр,д.,>о)

В,>0) + ...+ (7.27)

Хр-,А.->о)

в„. Ю-

В уравнении (7.27) сумма X7=oPoj.m(o0 ) вычисляется при помощи алгоритма де Кастильо по задающим точкам Р0 j. Алгоритм де Кастильо описан в приложе-

нии Е. Тем же методом вычисляются и все остальные суммы. Если обозначить их символами С0, Ci,..., С„, то уравнение (7.27) можно будет переписать так: Р(ы0 , б ) = С0В0>Я (ы0 ) + С, Ви (и0 >f.. .+С„Впп (и0 ) =

(7.28)

= £СД,>0).

Выражение (7.28) также может быть вычислено по алгоритму де Кастильо для задающих точек С,-.

7.5.2. Дифференцирование поверхности Безье

В системах геометрического моделирования часто возникает потребность в вычислении вектора нормали в произвольной точке поверхности. Например, для отображения затушеванного изображения поверхности необходимо определять угол между падающим светом и нормалью к поверхности в каждой ее точке. Векторы нормали также используются для вычисления положения фрезы при обработке поверхности станком с ЧПУ.

Итак, нам нужно уметь вычислять производные

8P(u,v) 8P(u,v) ди dv

в любой точке поверхности, поскольку вектор нормали определяется произведением этих частных производных. Вычислить производную по и для поверхности Безье в точках и = щ и v = v0 можно так, как показано ниже. Производная по v вычисляется аналогичным образом.

Дифференцируя выражение (7.23) по и, получим

dP(u,v) d

l о

£зд>)1в0,т(о)+

i=0 J

(7.29)

Перепишем коэффициент перед BQAV) в уравнении (7.29), используя результат из раздела 6.4.1 в следующем виде:

- du

-Т

(!- ) а

i,0 >

(7.30)

гдеа 0 =Р.+Ц) -р. .

Правую часть выражения (7.30) можно вычислить для произвольного значения щ по алгоритму де Кастильо (см. раздел 6.4.1). Тем же путем осуществляется вычисление коэффициентов Blm(o), B2m(v)> < BmAv) ДЛЯ щ. Если обозначить полученные значения коэффициентов символами С0, С С„, выражение (7.29) можно будет переписать в виде

дР(и v I m

- = C0B0m(v) + CtBlv)+...+CnBmM(p) = j:CjBj,m(v). (7.31)

Выражение (7.31) вычисляется также по алгоритму де Кастильо по задающим точкам С,-.

7.6. В-сплайновая поверхность

Подобно тому как от уравнения кривой Безье мы перешли к уравнению поверхности Безье, мы можем перейти и от уравнения В-сплайна к уравнению В-сплай-новой поверхности:

Р(и.я) = ХХР,.,АЛ )>) (**-. *н <tm+1), (7.32)

i=a >=о

где Pjj - задающие точки, расположенные в вершинах задающего многогранника, как и для поверхности Безье, a NiJt(u) и Njj(v) - функции сопряжения, используемые для построения В-сплайнов. Эти функции сопряжения определяются узловыми значениями s0, s sn+i и £0, th .... thm соответственно. Диапазоны параметров используются в определении В-сплайна, поскольку функции сопряжения NiJt(u) и Nji(v) определены только на этих интервалах, что уже демонстрировалось в главе 6. Это верно как для периодических узлов, так и для непериодических. Мы будем рассматривать только непериодические узлы по тем же причинам, что и раньше. В этом случае функции сопряжения В-сплайна будут совпадать с функциями сопряжения поверхности Безье, если k = n + i, I = m+l. Поэтому можно утверждать, что поверхность Безье является лишь частным случаем В-сплайновой поверхности, а уравнение (7.32) описывает как поверхности Безье, так и В-сплайновые. Чаще всего порядки k и / принимаются равными 4, поскольку степени уравнений, описывающих поверхности, не должны превышать 3.

В-сплайновая поверхность с непериодическими узлами обладает свойствами, напоминающими поверхность Безье (например, четыре угла задающего многогранника лежат на поверхности, а граничные кривые представляют собой В-сплайны, определяемые соответствующими подмножествами задающих точек). Покажем, что значению параметра и = 0 соответствует граничная кривая, являющаяся В-сплайном. Подстановка и = 0 в уравнение (7.32) дает1

Р(0,о) = 1

.1=0

9 JO

В соответствии с формулой (7.33), граничная кривая при и = 0 является В-сплай-ном с задающими точками Р00, Р0 .... Р0т. Аналогичным образом можно показать, что и остальные граничные кривые являются В-сплайнами, а их задающие точки являются крайними вершинами задающего многогранника.

7.6.1. Вычисление В-сплайновой поверхности

Координаты х, у и z точки на В-сплайновой поверхности, определяемой значениями параметров и = и0, v = v0, вычисляются по формуле

п m

РК.о ) = I lP, -AU o Wj.,(Mo ) (7-34)

1=0 ;=0

Выражение (7.34) можно переписать, раскрыв суммирование по г:

1 При выводе (7.33) использовался тот факт, что [£ =0PjNj,i,(m)]h=o =Ро-

P( o. o) =

W ,*( o) +

u( o)+--- +

1Р,,.,(р0)

(7.35)

Сумма XJ=oPoj.;(I,o) может быть вычислена при помощи алгоритма Кокса-де Бура по задающим точкам P0j и узловым точкам параметра v (см. приложение Ж). Обозначим эту сумму символом С0. Все прочие суммы вычисляются аналогичным образом и обозначаются С),С„. После этого становится возможным записать уравнение в форме

P(u0,v0) = C0NOJ,(u0) + ClNlJl(u0) +... +C N Jl(u0). (7.36)

Выражение (7.36) также вычисляется при помощи алгоритма Кокса-де Бура по задающим точкам С,- и узловым значениям и.

7.6.2. Дифференцирование В-сплайновой поверхности

По причинам, изложенным в разделе 7.5.2, достаточно часто возникает необходимость вычисления производных вида

8P(u,v) 8Р(и,у) ди do

в произвольной точке поверхности. Вычислить производную по и для В-сплайновой поверхности в точках и = щ и v = v0 можно так, как показано ниже. Производная по v вычисляется аналогичным образом.

Раскроем выражение (7.32), записав в явном виде сумму по j:

P(u,v) =

IPAUii)

(7.37)

NmJ(v).

Дифференцируя выражение (7.37) по и, получим 8P(u,v) d du

-1=0

IP,.oW,

-i=0

Nu(v)+...+ 1

N0J(P) +

£р|Л( )

(7.38)

Коэффициент перед N0l(v) в формуле (7.38) представляет собой производную В-сплайна с задающими точками р1>0 и может быть вычислен для произвольного значения и0 на основе соображений, изложенных в разделе 6.5.3. Обозначим значение этого коэффициента символом С0. Аналогичным образом вычисляются коэффициенты перед Nu(v), N2J(v), NmJ(v). Их мы обозначим С С2, С„. После этого выражение (7.38) можно будет записать так:

~ =CoNOJ(v) + ClNu(v) + ...+CmNmJ(v) = ZCjNjJ(v)- (7-39)

Выражение (7.39) мы вычислим также при помощи алгоритма Кокса-де Бура по задающим точкам Cj и узловым значениям v.

7.7. Поверхность NURBS

Перейдя к однородным координатам задающих точек, из уравнения В-сплайна мы получили уравнение NURBS-кривой. Точно так же уравнение поверхности NURBS получается из В-сплайновой поверхности:

Л 171

11р; лии)лг,>)

р( .е) = - (sk t <и<s +1, t, , <v<tm+i), (7.40)

i=0 y=0

где Pjj - векторы задающих точек с компонентами х, у и z, а - однородные координаты задающих точек. Обратите внимание, что узловые значения и диапазоны значений параметров совпадают с указанными в формуле (7.32).

Уравнение (7.40) становится уравнением В-сплайновой поверхности при кц = 1. Покажите самостоятельно, что при Лу = 1 знаменатель (7.40) тождественно равен единице. Следовательно, уравнение В-сплайновой поверхности является частным случаем уравнения NURBS-поверхности. Поверхность NURBS к тому же позволяет точно описать квадратичные поверхности, такие как цилиндр, конус, сфера, параболоид и гиперболоид. Эти поверхности называются квадратичными, потому что их уравнения имеют степень 2 по и и v. Уравнение NURBS-поверхности часто используется для внутреннего представления квадратичных поверхностей в системах геометрического моделирования.

Проиллюстрируем использование уравнений NURBS-поверхности в системах объемного моделирования на нескольких примерах. Первый пример: поверхность, полученная трансляцией кривой (рис. 7.6). Предположим, что транслируемая кривая задана NURBS-уравнением. Это предположение не накладывает никаких ограничений, поскольку уравнение любой кривой из рассмотренных нами может быть преобразовано к форме NURBS. Пусть порядок этой кривой /, узловые значения tp (р = 0, 1,...j m + /), задающие точки Pj (m + 1 штук).

ZhjPjNv)

р(е) = - (tH <v < С+1 ) (7.41)

Граничная кривая поверхности NURBS представляет собой NURBS-кривую с соответствующими задающими точками, которые являются крайними вершинами задающего многогранника поверхности. Порядок и узловые значения граничной кривой совпадают с теми же характеристиками поверхности в соответствующем направлении. Мы уже показали, что этим свойством обладают В-сплайновые поверхности. Следовательно, задающие точки, порядок и узловые значения поверхности в одном из направлений, совпадающем с направлением изменения параметра кривой, получаются из характеристик транслируемой кривой, поскольку она является одной из граничных кривых. В частности, задающими точками на

одном из краев поверхности будут точки Ру (рис. 7.6). Далее, порядок поверхности в направлении v будет равен /, а узловые значения будут равны tp (если направления параметров выбрать так, как показано на рис. 7.6).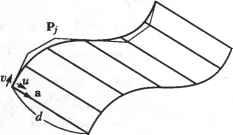

Рис. 7.6. Поверхность трансляции

Однако нам нужна информация о характеристиках поверхности в направлении и. Предполагается, что направление и совпадает с направлением трансляции (рис. 7.6), а значит, в этом направлении достаточно линейного уравнения. Следовательно, порядок NURBS-кривой в этом направлении будет равен 2 и задающих точек тоже будет две. Узловые значения в направлении и будут равны О, О, 1,1, а наборов узловых точек будет два. Один набор, как уже отмечалось, получается из Рр а второй набор получается трансляцией Pj на расстояние d в направлении трансляции. Однородные координаты для обоих наборов будут совпадать с hj транслируемой кривой. Итак, координаты х, у и z задающих точек Ptj и однородные координаты hij описываются следующими выражениями:

Pu=Pi+rfa; (7.42)

где d - расстояние трансляции, а а - единичный вектор в направлении трансляции.

Уравнение NURBS-поверхности может быть записано так, как показано ниже. Вычисление осуществляется подстановкой нужных значений параметров:

1 т

P(u,v) = -(0 < и < 1, r, , < v < tra+, ). (7.43)

IM) j=0

Обратите внимание, что Njj(v) в уравнении (7.43) определяется узловыми значениями tp.

NURBS-уравнение (7.43) может использоваться для представления любой поверхности, полученной трансляцией кривой. Например, это NURBS-уравнение может быть применено для описания цилиндрической поверхности, полученной трансляцией полуокружности, лежащей в плоскости ху, вдоль оси z (рис. 7.7). Сначала нам нужно задать NURBS-представление полуокружности. Воспользу-

емся результатами примера 6.6. Задающие точки будут иметь следующие координаты:

Р0 =(1.0,0), А0 =1; Р, =(1,1,0), А, =-Ь Р2 =(0,1.0), А2 =1; Р3 =(-1,1,0), Л, = -j=;

Р4 =(-1,0,0), А4 =1.

порядок кривой должен быть равен 3, а ее узловые значения равны 0, 0, 0, 1,1, 2, 2, 2. Координаты задающих точек цилиндрической поверхности будут такими:

где Р0,о, Po,i> Ро,2. Ро,з и Ро,4 обозначают задающие точки нижней дуги, а Р, 0, Р , Р,2, P13 и Р,4 - задающие точки верхней дуги; k - единичный вектор в направлении оси z. NURBS-уравнение цилиндрической поверхности получается подстановкой Pjj и hij в уравнение (7.43) с учетом того, что / = 3 и т = 4. Узловые значения в направлении v равны 0, 0, 0, 1, 1, 2, 2, 2, а в направлении и они равны 0, 0, 1, 1.

Рассмотрим другой пример - поверхность вращения. Пусть вращаемая кривая лежит в плоскости xz, ось вращения совпадает с осью z, а направление кривой совпадает с направлением параметра v создаваемой поверхности (рис 7.8). Предположим, что мы имеем дело с NURBS-кривой порядка / с узловыми значе-

ниями tp (р - О, 1,.... т + Г) и задающими точками Р,(га + 1 штук) и /г, (однородные координаты задающих точек). Можно предположить, что каждая задающая точка Pj разделится на девять задающих точек, определяющих круговое поперечное сечение (рис. 7.8).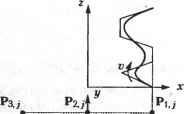

P5,j Рб,> Р7,У

Рйс. 7.8. Поверхность вращения

Подробное описание этого метода приводится в работе [126]. Девять задающих точек поверхности имеют следующие координаты:

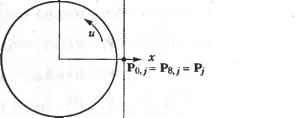8 m

Х1Р,ЛГ,3(Ы)Л ;(р)

P( ) = i=r->- (0 < и < 4, r, , < v < tm+l ). (7.44)

11А;ЛГ,з( )Л0.,(гО

i=0 y=0

Обратите внимание, что порядок поверхности в направлении и равен 3, потому что степени 2 достаточно для представления окружности. Узловые значения Njt получаются из NURBS-представления вращаемой кривой, а узловые значения Ni3 следуют из узловых значений представления полуокружности: 0, 0, 0, 1, 1, 2, 2,3, 3, 4, 4, 4.

Чтобы вычислить координаты х, у и z точки на NURBS-поверхности, мы должны подставить соответствующие ей значения параметров и = щ и v = v0 в уравнение (7.44). Тогда мы сможем заметить, что числитель и знаменатель в этом выражении имеют тот же вид, что и в уравнении В-сплайновой поверхности. Поэтому мы можем воспользоваться методом для вычисления В-сплайновых поверхностей, правда, с небольшим изменением для учета однородных координат: при вычислении числителя Kji.j подставляется вместо P,j, а при вычислении знаменателя hjj подставляется вместо P(J-.

Кроме того, можно вычислить производные NURBS-поверхности, применив методы, использованные для вычисления В-сплайновой поверхности и ее производных. Проверку этого утверждения предоставляем читателю в качестве упражнения.

7.8. Интерполяционная поверхность

Мы уже рассматривали проблему создания кривой, проходящей через заданные точки, - интерполяционной кривой. Часто возникает необходимость построения поверхности, проходящей через заданные точки. Особенно часто это требуется при создании геометрической модели по существующей физической. Существует множество методов интерполяции точек данных; эти методы основаны на различных уравнениях интерполяционных поверхностей. В этом разделе мы выведем уравнение В-сплайновой поверхности, проходящей через заданные точки.

Обозначим точки 0рЯ (р = 0, 1,.... и; q = 0, 1,.... га) в соответствии с рис. 7.9. Поскольку эти точки накладывают (и + 1)х (га+ 1) ограничений, можно выбрать любую В-сплайновую поверхность с числом задающих точек не менее (n + 1) х (т + 1). Для простоты мы рассмотрим В-сплайновую поверхность, число задающих точек которой в точности равно указанному произведению.

17 177

Р(и. ) = I iPyB)., (7.45)

1=0 j=0

где Р j - задающие точки. Пусть каждой заданной точке Qpq соответствуют значения параметров ир и vgi, тогда

п т i=0 7=0

Значение ир может быть получено методом, описанным в разделе 6.7.2 из узловых значений, определенных в процессе интерполяции точек Qo4, Qi. Q ., В-сплайном. Точно так же и vq получается из узловых значений после интерполяции Qtj.o, Q/>,i> -. Qp.m-

Можно переписать выражение (7.46), обозначив ЦоРу.;)символом С,<о,):

Q0,m О**,

Qo.i

Орд

Рис. 7.9. Интерполяция заданных точек Подстановка значений q = 0...т в выражение (7.47) дает

%.о =£c,(v0)NtJt(iip);

=ZCj(p1),t(M,));

(7.47)

(7.48)

Подставив значения p = 0...П в первую строку выражения (7.48), мы получим задающие точки Cj(v0) (i = 0, 1,п) В-сплайна, интерполирующего точки Qo,0, Qi,o,

Qo..... Qo, - первой горизонтальной кривой на рис. 7.10. Аналогично, С,(с,)

(i = 0, 1, и) - задающие точки В-сплайна, интерполирующего точки Qo.i, Q , Q, 1,.... Qj,!, - второй горизонтальной кривой на том же рисунке, и т. д. Эти задающие точки интерполяционного В-сплайна получаются методом, описанным в разделе 6.7.2.

Теперь вычислим задающие точки Pv- по С,(а9) (q = 0, 1, га). Для этого запишем определение Ct(vq) еще раз:

С,К) = 1Р,.,Л^,). (7.49)

Если теперь подставить значения q = 0...га в формулу (7.49), мы обнаружим, что Ру - задающие точки В-сплайиа, интерполирующего точки С,(а0), C;(#i), -, Ci(vm). В частности, точки P0j - это задающие точки В-сплайна, интерполирующего C0(v0), С0(с,).....C0(vm), крайние слева точки на рис. 7.10.

Приведем краткое описание процедуры вывода значений Pw-:

□ заданные точки интерполируются В-сплайном в одном направлении (рис. 7.10); *

□ задающие точки В-сплайнов, полученных на первом этапе, интерполируются в поперечном направлении: берутся i-e задающие точки всех В-сплайнов из

первого этапа и интерполируются В-сплайном. Задающие точки нового В-

сплайна будут Р,-,о, P i, Р 2..... Р.\т- Повторив эту процедуру для всех i от 0

до и, мы получим все задающие точки Pw.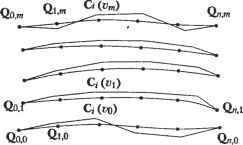

Рис. 7.10. Точки C,{vq), получаемые интерполяцией в направлении и

Получив все задающие точки интерполяционной поверхности, мы должны определить порядки k и / и узловые значения в направлениях и и v соответственно. Чаще всего используются поверхности степени 3 по и и v, поэтому обычно берутся значения k = l=A. Мы знаем, что узловые значения получаются в процессе вывода интерполяционной кривой (см. раздел 6.7.2). Таким образом мы получаем га + 1 наборов узловых значений в направлении и от всех интерполяционных кривых с рис. 7.10. Из этих наборов можно получить один путем усреднения. Другими словами, i-e узловое значение получается усреднением i-x узловых значений из каждого из га + 1 наборов. Узловые значения в направлении v получаются аналогичным образом.

7.9. Пересечение поверхностей

В этом разделе мы займемся вычислением кривых пересечения поверхностей. Из-за внутренних ограничений численных методов мы будем искать точки на кривых пересечения. Мы уже говорили, что кривые пересечения поверхностей нужны нам для реализации булевских операций. Кривые пересечения требуются также для реализации отсечения поверхностей другими поверхностями в системах поверхностного моделирования. Мы кратко изложим основные идеи, лежащие в основе алгоритмов для расчета кривых пересечения поверхностей, заданных параметрическими уравнениями. Мы рассматриваем только параметрические уравнения, поскольку именно они чаще всего используются для представления поверхностей.

Методы расчета кривых пересечения поверхностей могут быть разделены на два класса. Методы первого класса состоят в численном решении приведенного ниже нелинейного уравнения:

P(H,a)-Q(s,O = 0, (750)

где Р(м,с) и Q(s,£) - параметрические уравнения пересекающихся поверхностей. Уравнение (7.50) распадается на три скалярных уравнения с четырьмя неизвестными: и, v, s и t. Решение этой системы требует присвоения произвольного значения одному из параметров. При этом получаются значения параметров, соответ-

вующие точке на кривой пересечения. Изменение выбранного произвольного гачения дает все остальные точки кривой пересечения. Недостаток этого мето-i в том, что его сходимость зависит от начальных приближений неизвестных в >авнении (7.50) [49]. Более того, он не всегда позволяет найти все кривые пере- чения. Другими словами, при больших интервалах изменения произвольно за-изаемого параметра некоторые кривые могут быть потеряны полностью, а неко->рые - частично.

[етоды из второй категории основаны на теории последовательного деления [37]. аждая поверхность последовательно делится на множество частей до тех пор, эка каждая из них не будет представлять собой нечто близкое к плоскому четы-;хугольнику. Затем четырехугольники одной поверхности проверяются на пе-гсечение с четырехугольниками другой поверхности. В результате получаются ары пересекающихся четырехугольников, а точки прямых, по которым они пе-гсекаются, дают хорошее начальное приближение для уравнения (7.50). Одна-э может оказаться непросто проверять пары четырехугольников в правильной □следовательности так, чтобы точки пересечения образовывали кривые. Для реодоления этой проблемы был предложен альтернативный подход [124, 90]. методе Пенга из всех четырехугольников пересекающихся поверхностей выби-ается лишь одна пересекающаяся пара, которая дает первый сегмент кривой пе-есечения. Один из концов этого сегмента берется в качестве начальной точки, г которой производится поиск следующей точки пересечения. Другими сло-ами, ищется новая пара четырехугольников, которая даст соседний сегмент ривой пересечения, одним из концов которого будет начальная точка поиска, [ересечение новой пары четырехугольников даст две точки, одна из которых бе-ется в качестве нового конца кривой, от которого начинается поиск следующей ары четырехугольников. Пенг хранил четырехугольники в квадрантном дереве1 quadtree), предложенном Саметом [135] для повышения эффективности поиска оседней пары. Процедура поиска продолжается до тех пор, пока не будет до-гигнута одна из границ поверхности, после чего поиск начинается с другого кон-а первого сегмента. Точные координаты точек пересечения получаются реше-ием уравнения (7.50) с использованием концов сегментов в качестве начально-о приближения. Эта процедура повторяется со всеми начальными сегментами о тех пор, пока не будут найдены все кривые. В приложении К мы расскажем, аким образом следует искать все сегменты кривых пересечения.

Методы, основанные на теории последовательного деления, требуют большего бъема вычислений по сравнению с методами первого класса, но зато они реже ропускают кривые пересечения. В приложении К мы рассмотрим расчет пере-ечения NURBS-поверхностей по методу Пенга.

вопросы и задачи

- Коническая поверхность получается вращением отрезка, соединяющего точки (2, 0, 0) и (1, 2, 0) вокруг оси у на 180°.

Квадрантное дерево представляет собой двумерный аналог октантного дерева. Прямоугольник, описывающий исходный объект, последовательно делится на четыре части до тех пор, пока не будет достигнуто нужное разрешение.

1) Получите параметрическое уравнение конической поверхности. Предпо-, ложите, что изменение параметра и перемещает точку по окружности на

плоскости, перпендикулярной оси у, а параметр с изменяет положение окружности относительно этой оси.

2) Аппроксимируйте коническую поверхность бикубическим лоскутом. Другими словами, вы должны вывести матрицу геометрических коэффицен-тов для формулы (7.18).

3) Вычислите координаты точки бикубического лоскута, соответствующей значениям параметров и = 0,5 и v = 0,5, и сравните ее с результатом вычисления по точному параметрическому уравнению.

2. Представьте поверхность, изображенную на приведенном ниже рисунке, билинейной поверхностью.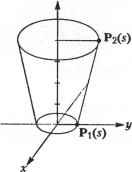

1) Определите Pi(s) и РгСя), описывающие окружность при изменении s от 0 до 1.

2) Представьте коническую поверхность функцией r(s,t), осуществляющей линейное сопряжение P,(s) и P2(s). Пусть параметр с также меняется от 0 до 1.

3) Подставьте значение г = 0,5 в функцию r(s,t) и объясните, что при этом получается.

3. Аппроксимируйте поверхность, ограниченную тремя дугами (см. рисунок), при помощи лоскута Куна.

Центры всех дуг расположены в начале координат. Вы можете разделить окружность, лежащую в плоскости ху, в точке (0, 1, 0), чтобы получить четыре граничные кривые. Уравнения граничных кривых следует записывать аккуратно, чтобы их направление соответствовало принятому при выводе уравнения лоскута Куна.

4. Цилиндрическая поверхность получается сдвигом дуги, лежащей в плоскости ху, вдоль оси г на 4 единицы (см. рисунок). Радиус дуги в четверть окружности равен 1, а ее центр находится в точке с координатами (0, 0, 0). Выполните следующие действия.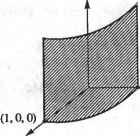

(0,1,0)

У

х

1) Выведите точное параметрическое уравнение цилиндрической поверхности. Определите параметры и и v так, чтобы они давали всю поверхность при изменении от 0 до 1.

2) Аппроксимируйте цилиндрическую поверхность лоскутом Куна.

3) Аппроксимируйте цилиндрическую поверхность бикубическим лоскутом.

4) Аппроксимируйте цилиндрическую поверхность лоскутом Ферпосона.

5) Сравните поверхности из предыдущих пунктов с точной поверхностью в средней точке параметров иис.

5. Представьте цилиндрическую поверхность из пункта 4 в форме NURBS. Вы должны определить узловые значения и порядки в направлениях иис,а также координаты задающих точек (в том числе однородные).

6. Представьте цилиндрическую поверхность из пункта 4 уравнением Безье.

1) Аппроксимируйте четверть окружности кривой Безье, определяемой тремя задающими точками.

2) Определите задающие точки поверхности Безье.

3) Сравните координаты точки, соответствующей средним значениям параметров, с результатами из пункта 4.

Глава 8

Метод конечных элементов

В современном проектировании широко используются различные программные пакеты автоматизированного конструирования (computer-aided engineering - CAE), позволяющие оценивать проекты на каждом этапе процесса разработки. Средства CAE позволяют анализировать кинематику или динамику поведения проектируемого агрегата. К этой категории относятся такие пакеты, как ADAMS и DADS (см. главу 2). С точки зрения этих пакетов каждый компонент агрегата рассматривается как тело с сосредоточенной массой. В некоторых случаях средства CAE позволяют определить распределение напряжений или температур в механических компонентах, рассчитанных на физическую или тепловую нагрузку. Возможно также проведение вибрационного анализа компонента, на который будет воздействовать динамическая нагрузка. Перечисленные задачи решаются при помощи средств анализа методом конечных элементов. Примерами коммерческих программ конечноэлементного анализа являются NASTRAN и ANSYS (см. главу 2).

На заре своего существования метод конечных элементов применялся главным образом в строительной механике. Словосочетание конечный элемент (finite element) появилось в статье Клофа [36], где предлагалось применять новый метод для анализа напряжений в плоскостях. Многие коммерческие пакеты, основанные на методе конечных элементов, изначально предназначались для решения строительных задач. Однако вскоре стало ясно, что методы конечных элементов имеют более широкую область применения: задачи теплопереноса, распределения электростатического потенциала, механики жидкостей, вибрационного анализа и многие другие. С ростом вычислительных возможностей компьютеров расширился диапазон и возросла сложность задач, доступных решению методом конечных элементов. Применение метода конечных элементов к дверной ручке холодильника для расчета распределения температуры при заполнении формы для литья под давлением жидкой пластмассой демонстрирует рис. 8.1. В качестве примеров программ для решения задач механики жидкостей методом конечных элементов можно привести пакеты C-MOLD и MOLDFLOW, предназначенные для моделирования течения жидкого пластика в форме для литья под давлением.

Главное отличие метода конечных элементов от динамического или кинематического анализа заключается в том, что в первом область задачи рассматривается как непрерывное пространство (континуум), а во втором - как набор дискретных (сосредоточенных) элементов. В этой главе мы изучим основные концепции средств анализа методом конечных элементов. Мы не станем уделять внимание

средствам кинематического или динамического анализа, поскольку программы этого типа просты для понимания и для работы с ними вполне достаточно руководства пользователя.

Рис. 8.1. Распределение температуры, полученное методом конечных элементов

8.1. Введение в метод конечных элементов

В реальных конструкциях почти всегда присутствуют сложные формы, состоящие к тому же из различных материалов. В качестве примера рассмотрим задачи, представленные на рис. 8.2. Рассчитать распределение напряжений в кронштейне (рис. 8.2, а) при помощи аналитических методов крайне сложно. Если же кронштейн изготовлен из композитного материала со сложными свойствами, задача становится практически неразрешимой. Непреодолимые затруднения возникают и при попытке вывести аналитическое выражение для распределения температур в объекте, изображенном на рис. 8.2, б.

Метод конечных элементов, по всей видимости, является наиболее популярным численным методом решения таких задач. Универсальность этого метода удовлетворяет требованиям современных сложных систем конструирования, для которых обычно отсутствуют замкнутые решения уравнений равновесия. Анализ методом конечных элементов начинается с аппроксимации исследуемой области

(области задачи) и делении ее на ячейки сетки. На рис. 8.3, а по углам каждой ячейки находятся узлы (черные точки). Такие ячейки и называются конечными элементами. На рис. 8.3, а, б представлены аппроксимации объектов с рис. 8.2, а, б наборами конечных элементов (треугольных и четырехугольных).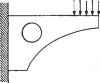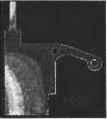

а б

Рис. 8.2. Задачи, не имеющие аналитического решения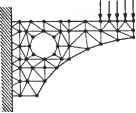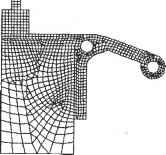

Рис. 8.3. Аппроксимация объектов конечными элементами

В этом примере мы аппроксимировали исходный объект треугольниками и четырехугольниками, однако возможны и конечные элементы других типов. Вы бор элементов определяется областью задачи, ее типом, а также конкретным пакетом анализа. Выбор подходящих элементов с нужным количеством узлов из библиотеки доступных элементов является одним из наиболее важных решений, которые приходится принимать пользователю пакета конечноэлементного анализа. Конструктору также приходится задавать полное количество элементов (другими словами, их размер). Общее правило состоит в том, что чем больше количество узлов и элементов (в /г-версии1) или чем выше степень функции фор-

1 Классическая форма метода конечных элементов называется h-версией. В качестве функции формы в этой версии используются кусочные полиномы фиксированных степеней, а повышение точности достигается уменьшением размеров ячеек. В р-версии используется фиксированная сетка, а точность повышается благодаря увеличению степени функции формы. Подробнее см. в работах [103. 148].