ружности - это квадратичная кривая степени 2, поэтому можно предполагать, что ее NURBS-представление будет иметь степень 3. Пигл показал, что если центральный угол дуги окружности меньше 180°, для представления этой дуги достаточно всего лишь трех задающих точек (рис. 6.8). Из рассмотренных ранее свойств NURBS-кривых следует, что задающие точки Р0 и Р2 должны располагаться на концах дуги окружности, а точка Р| находится в точке пересечения касательных к дуге в ее конечных точках.

Рис. 6.8. Задающие точки NURBS-представления дуги окружности

Остается определить однородные координаты hG, h\ и h2. Если бы все они были равны 1, это был бы обычный В-сплайн, который не мог бы совпадать с дугой окружности. Однако Пигл обнаружил, что значения h0 = h2 = 1, hx = cos G позволяют описать дугу точно. Здесь буквой G обозначен угол между любой касательной и отрезком РоРг (см. рис. 6.8). Отсюда следует, что для центрального угла дуги, превышающего 180°, точка Р1( а значит, и угол G оказываются не определены. В этом случае дугу нужно разделить на части таким образом, чтобы у каждой из этих частей центральный угол был бы меньше 180°. Затем для каждой части определяется NURBS-представление, после чего эти представления объединяются. Объединение NURBS-кривых получается точно таким же способом, что и объединение В-сплайнов (см. приложение 3). Множество задающих точек объединенной кривой представляет собой объединение множеств задающих точек исходных кривых. Узловые значения объединенной кривой получаются слиянием наборов узловых значений с предварительным их сдвигом, обеспечивающим отсутствие скачков в точках соединений. Затем лишние узловые значения отбрасываются так, чтобы для каждого соединения значения повторялись не более чем k - 1 раз.

Пример 6.6

Вывести NURBS-представление полуокружности с единичным радиусом, расположенной в плоскости ху. Необходимо определить степень кривой, координаты задающих точек, а также узловые значения.

Решение

Изучите приведенный ниже рисунок. Порядок NURBS-кривой должен быть равен 3, поскольку окружность - квадратичная кривая. Мы разделим полуокружность на две дуги с номерами 1 и 2, поскольку центральный угол полуокружности равен 180°. Разделить ее, разумеется, можно множеством способов.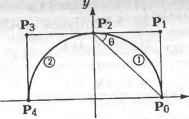

Начнем с дуги 1. Координаты х, у, z задающих точек этой дуги таковы:

Р0 =(1,0), Р, =(1,1), Р2 =(0,1). Соответствующие однородные координаты имеют значения h0 = 1, hx = cos 45° = = 1/2 и h2 = 1. Узловые значения параметра образуют последовательность 0, 0, 0, 1,1,1 (и = 2. * = 3). Та же процедура для дуги 2 дает

и

р„=(од> р3 =<u> p =a°)

h2 =1, h3 =-j=, к =i-

Узловые значения те же самые: 0, 0, 0, 1, 1, 1, но для последующего объединения кривых они сдвигаются до 1, 1, 1, 2, 2, 2.

NURBS-кривые объединяются вместе, в результате чего получается NURBS-кривая со следующими задающими точками и параметрами:

и

р0=(1,о), р,=(1Д), p2=(o,i> p3=(-U), p4=(-i.o) л0 =1, К = ±, h2=i, h3=± ft,-!.

V *

Узловые значения для объединенной кривой: 0, 0, 0, 1, 1, 2, 2, 2. Пример 6.7

Раскрыть уравнение NURBS-представления дуги 1 из примера 6.6 и показать, что оно действительно .точно соответствует дуге окружности.

Решение

Уравнение NURBS-представления дуги 1 имеет вид:

= h0P0N03(u)+ hlPtNl3(u) + h2P2N2 (u) h0N03(u)+hlNt3(u)+ h2Nri(u)

Функции сопряжения N03(u), N13(u) и N23(u) получаем по рекуррентным соотношениям:

Nu(u) = NZ2(u) =

1 0<м<1ж

О в противном случае;

= (1-и);

и;

= d- )2;

(u-tl)Nl2(u) (t4 -u)N22(u)

-Tt- -~T~t-=2 (1- );

L3 ll rt -t2

(u-t2)N22(u) 2 =-t~t-= U

Теперь мы можем записать уравнение NURBS-представления следующим образом:

Р(и) =

1.(1-и)* +.2М(1-Ы)+1.Ы2

Обозначим члены, соответствующие х и г/ в этом уравнении, за л(к) и г/(ы) соответственно. Выражения для х(ы) и у(и) будут такими:

(2-л/2)ы2 +(л/2-2)ы + 1

У(и) =

(1-л/2)ы2 +л/2ы

(2-л/2)ы2 +(л/2-2)ы + 1 Можно показать, что х(ы) и гу(ы) удовлетворяют равенству

{х(и)}2 +{у(и)}2 {Q-2+(l-) + l}2+{(l-,/2)+M}2

{(2-л/2)ы2 +(л/2-2)ы + 1}2

Отсюда следует, что представление NURBS-кривой в точности совпадает с дугой окружности.

6.1. Вычисление NURBS-кривой

Координаты х, у, z точки на NURBS-кривой, определяемой значением параметра Щ, получаются по формуле:

Р(Ыо) = Р -.

(6.52)

И числитель, и знаменатель в выражении (6.52) имеют форму уравнения В-сплайна, поэтому они могут вычисляться по алгоритму, предназначенному для вычисления В-сплайна. Алгоритм Кокса-де Бура приводится в приложении 3. При вычислении числителя в качестве задающих точек следует брать точки с координатами h,Pj, а при вычислении знаменателя - точки hr

6.6.2. Дифференцирование NURBS-кривой

Производная первого порядка от кривой в NURBS-представлении может быть получена дифференцированием уравнения (6.51) по и:

dP(u) du du

JhNu)

.1=0

IAU-IMW.*(K)--f

,=o i=0 йи

.1=0

[£ X*( )12

(6.53)

Выражения XLAi.t(M) и X =oP.*(M) в формуле (6.53) могут быть вычислены с использованием алгоритма для В-сплайнов, например алгоритма Кокса-де Бура, который излагается в приложении 3. Производные в числителе могут быть получены по методу, который был изложен в разделе 6.5.3. А именно, вместо задающих точек Р,- в уравнение (6.44) следует подставить й,-Р,- при вычислении

или hj при вычислении

d du

d du

Пример 6.8

Раскрыв выражение (6.51), показать, что NURBS-кривая с непериодическими узлами проходит через первую и последнюю задающие точки. Используя уравнение (6.53), показать, что касательные к NURBS-кривой в конечных точках совпадают по направлению с векторами Р| - Р0 и Р„ - Р„ ,.

Решение

Начальной точке кривой NURBS соответствует значение параметра to = =... = 4-i-Первому сегменту соответствует диапазон значений параметра tk-\Utk, а к-\л ~~ единственная ненулевая функция сопряжения первого порядка на этом интервале, то есть единственная функция данного порядка, которую имеет смысл рассматривать в вычислениях, связанных с данным сегментом. Отсюда все функции сопряжения Л^ (4 ) нулевые, за исключением N0,k(tk.,), значение которой равно единице. Проверить последнее утверждение можно по рекуррентной формуле. Итак, из уравнения (6.52) мы можем найти начальную точку кривой:

Конечной точке кривой будут соответствовать значения параметра 4+, = 4+2 = ... = t +k. Поскольку N , - единственная ненулевая функция сопряжения первого порядка на отрезке 4 и 4+ она одна должна учитываться при выводе уравнения последнего сегмента кривой. И она же будет ненулевой при и = t +l. Отсюда все функции сопряжения вида (4+,) равны нулю, за исключением iV -t(4+i) = 1- Следовательно, координаты конечной точки могут быть получены из уравнения (6.52) в следующем виде:

у

ZMW.*(4+i) hPN (t ч i.p 1

Получить первую производную в начальной точке можно с помощью уравнения (6.53). Левая производная в числителе (6.53) вычисляется подстановкой /г,Р, вместо Р{ и h0P0 вместо Р0 в конечное выражение примера 6.5. Точно так же правая производная вычисляется подстановкой ht вместо Р| и h0 вместо Р0. Далее, Х =оА \*(**-1) = о- Из всего вышеизложенного следует, что первая производная в начальной точке кривой равна

dP(u)

(б-1)Лр< A4iPo(M).H.

t -t[ 1 0 (*-!)*,

(P.-Po)-

Аналогичным образом вычисляется первая производная и в конечной точке.

6.7. Интерполяционные кривые

Представьте, что вы работаете в системе геометрического моделирования и хотите визуализировать кривую. Кажется естественным передать системе координаты нескольких точек на этой кривой. На самом деле чертежники рисуют кривые таким интуитивным методом уже многие годы. Они ставят на бумаге несколько точек в соответствии со своим представлением о форме кривой, а затем соединяют их плавной линией при помощи средства, называемого сплайном (spline). Так же и в САПР: конструктор указывает точки, а система строит по ним интерполяционную кривую, которую и отображает. Уравнение интерполяционной кривой сохраняется для последующей работы с ней. Можно создать кривую, непосредственно указав задающие точки кривой Безье или В-сплайна. Однако большин-

ство конструкторов предпочитают указывать точки, лежащие на самой кривой, и изменять кривую, перемещая ее характеристические точки. Характеристическими точками могут быть задающие точки кривой Безье или В-сплайна, если интерполяционная кривая относится к одному из этих классов. Возможность строить интерполяционные кривые по точкам очень полезна, если геометрическая модель создается по существующей физической модели. Представьте, что нам нужно получить математическое описание кривых и поверхностей пластилиновой модели автомобиля. Математическое описание поверхностей может применяться для автоматической выработки траекторий движения фрезы с ЧПУ. Вот в такой ситуации нам и пригодится функция построения поверхностей и кривых по точкам. Перейдем же теперь к выводу уравнений интерполяционных кривых - эрмитовой кривой и В-сплайна.

6.7.1. Интерполяция эрмитовой кривой

Основная идея данного метода заключается в том, что каждый сегмент между соседними точками представляется в виде эрмитовой кривой. Поскольку степень такой кривой равна 3, этот подход аналогичен использованию сплайна (рис. 6.9) для проведения кривой по заданным точкам.

Рис. 6.9. Сплайн - инструмент, применяемый в черчении

Сплайн, проведенный через заданные точки, имеет физический аналог - балку с подпорками в тех же заданных точках (рис. 6.10). Форма любого сегмента между ближайшими опорами определяется уравнением балки:

d2y Q0x+M0 5J

dx2 EI

Рис. 6.10. Статическая модель сплайна

Уравнение (6.54) является дифференциальным, ему должна удовлетворять нейтральная линия балки, находящейся под влиянием силы реакции Од и момента М0, приложенных к левой опоре. Здесь под Е понимается модуль Юнга материала, из которого изготовлена балка, а / - момент инерции ее поперечного сечения. Двойное интегрирование уравнения (6.54) дает функцию у(х), степень которой равна 3. Поэтому для описания сегментов кривой между точками может использоваться эрмитова кривая.

1 Вывод уравнения (6.54) можно найти в любом учебнике по сопротивлению материалов

Выведем уравнение эрмитовой кривой для всех сегментов при условии, что мы знаем координаты точек Р0, Р|, ... , р„. Эти п + 1 точек дадут нам п эрмитовых кривых, которые мы обозначим буквами Р\(и), Рг( ).....рп( ) (рис. 6.11).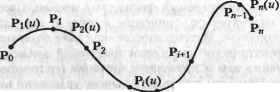

Pi+i( ) Р.--1 р. -

Рис. 6.11. Интерполируемые точки и эрмитовы кривые

Эрмитова кривая под номером i может быть записана с использованием уравнений (6.10) и (6.12):

й(*0-Рм +р> + [3(р, -рм)-2р; , -р>2 + +[2(рм -р,) + рм+р>3.

(6.55)

Здесь р? , и Р\ - векторы касательных в точках р, , и р, соответственно. Уравнение для конкретного сегмента получается подстановкой конкретного значения i в общее уравнение. Для каждого сегмента параметр изменяется от 0 до 1.

При попытке воспользоваться уравнением (6.55) мы столкнулись бы с одним затруднением: коэффициенты р- , и р, обычно не указываются. Поэтому нам нужно изменить уравнение (6.55) так, чтобы они в нем и не появлялись. Чтобы иметь возможность вычислить производные р, , и р/ по самим данным, нам нужно наложить граничное условие, гарантирующее непрерывность производной второго порядка в точках соединения сегментов кривой:

d%(u)

d2Pul(u)

0 = 1,2.....n-l).

Подстановка (6.55) в (6.56) дает

2(-зрм + зр, -2р; , -р;)+б(2рм -2р,. +р; , +р;) = = 2(-зр1+зр1+1 -2р;-р;+1).

(6.56)

(6.57)

Первая строка в уравнении (6.57) получается двойным дифференцированием уравнения (6.55) и подстановкой значения и = 1. Вторая строка получается тем же путем после получения выражения для р1+,(и) после подстановки i + 1 вместо г в уравнение (6.55). Упрощение (6.57) дает следующее выражение:

р;, +4р;+р;+1 =зр1+1 -зр . (6.58)

Подставляя в уравнение (6.58) все значения i от 1 до п - 1, мы получим приведенное ниже матричное уравнение:

4 10.. 14 10 0 14 10

0 0 0 0

о

о

.n-l

зр2 зр0 р0 зр3 -зр, зр4 -зр2

зр -2 -К j

(6.59)

Если нам известны значения р^ и Р'п из правой части уравнения (6.59), мы можем найти значения п - 1 неизвестных переменных р р2.....р', ,. Получив значения всех производных, мы можем подставить их в уравнение (6.55) и получить, таким образом, полностью определенную эрмитову кривую.

Осталось определить Р'0 и Р'п, то есть векторы касательных на концах кривой. Для этого обычно выбирают один из двух методов, однако от этого выбора зависит форма интерполяционной кривой. В первом случае конструктор задает направления касательных вручную. Говорят, что на кривую накладывается условие жестко закрепленных концов. Второй метод состоит в предположении об отсутствии крутящих моментов на концах балки. Это эквивалентно присваиванию р' 0 и р' нулевых значений, поскольку вторая производная пропорциональна крутящему моменту. Отсюда получаются приведенные ниже дополнительные уравнения, выражающие заданное ограничение:

</2р,(и)

du2 </2р

= -зр0 +зр, -2р; -р; =о.

= 2[3(рп-р„ 1)-2ри.,-рп] +

(6.60)

(6.61)

+ б[2(р„ , -рп)+р^, +р;].

Упрощение выражений (6.60) и (6.61) дает:

2р0+р; =зр, -зр0;

2р;и +р; , =зр -зр .,.

Перепишем матричное уравнение (6.59), переставив Р'0 и Р'п в левую часть и добавив уравнения (6.62) и (6.63) в начало и конец матрицы соответственно. В результате получится новое матричное уравнение:

(6.62) (6.63)

1 4 1

о

о о

р' Pi

зр, -зр0 зр2 -зр0 зр3 - зр,

(6.64)

Уравнение (6.64) позволяет найти п + 1 неизвестных: Р'0,Р[,...,Р'п.

Различия между двумя интерполяционными кривыми, построенными по одним и тем же точкам, иллюстрирует рис. 6.12: у одной кривой конец жестко закреп-

лен, а у другой - свободен. Обратите внимание, что интерполяционная кривая со свободными концами как бы распрямляется вблизи них.

Закрепленный конец

Рис. 6.12. Зависимость интерполяционных кривых от граничных условии

6.7.2. Интерполяция В-сплайном

В этом разделе мы рассмотрим вывод уравнения В-сплайна, проходящего через точки Qo, Qi,.... Q . Нам придется определить степень, количество задающих точек, их координаты, а также узловые значения параметра интерполяционного В-сплайна. Любой В-сплайн, определяемый п + 1 и более задающими точками, можно провести через и + 1 точек, потому что у такой кривой будет п + 1 и более степеней свободы. В-сплайн с большим числом степеней дает конструктору большую свободу в управлении формой кривой, например направлением касательных на ее концах. В этом разделе для простоты мы рассмотрим только В-сплайн с п + 1 задающими точками.

Сначала нужно выбрать порядок В-сплайна. Чаще всего выбирается порядок 4, поскольку степень 3 является минимальной, удовлетворяющей требованию непрерывности второй производной в точках соединения. Затем определяются узловые значения. Поскольку мы решили работать с п + 1 задающими точками, нам придется вычислить п + k + 1 узлов. Узлы можно выбрать множеством спо-эв, так что мы воспользуемся результатами Хартли [63] и Ли [98]:

=0 (г=0,1,...,*-1);

=.-.+7,- = * + !,....*); (6-65)

I. И

m=kj-m-k

t. =1 (i = w + l,w + 2.....n + k),

где

dj = VQ,+1 -Qj\. (6-66)

Пусть нам нужно определить положение п + 1 задающих точек Р0, Рц Рп- Эти точки должны удовлетворять соотношению:

% = tftfiXMj ) U =0,1,.... п), (6.67)

где Uj - значения параметра, которые должны соответствовать точкам Q,. Любой набор uj между и t +i даст В-сплайн, проходящий через точки данных. Однако

гладкость этого В-сплайна будет очень сильно зависеть от выбора щ. Хартли [63] рекомендует для получения гладкой кривой выбирать следующие значения и/.

0=0,1.....n).

(6.68)

Значения ujt полученные из уравнения (6.68), подставляются в формулу (6.67), в результате чего получается следующий набор уравнений для Р,:

(6.69)

Решение (6.69) относительно Р, позволяет получить координаты задающих точек В-сплайна, проходящего через точки Q,.

6.8. Пересечение кривых

Мы уже показали, что для реализации булевских операций необходимо уметь рассчитывать точки пересечения кривых. Точку пересечения приходится также определять для отсечения части кривой другой кривой. В этом разделе мы кратко изложим основные сведения об алгоритмах поиска точек пересечения кривых, заданных параметрическими уравнениями. Описанный метод может использоваться для расчетов с произвольными кривыми следующих типов: эрмитовы кривые, кривые Безье, В-сплайн и NURBS. Методы расчета точек пересечения для кривых, заданных не параметрически, а также для кривых с уравнениями разных типов (параметрическими и непараметрическими) излагаются в работе Хоффманна [69].

Предположим, что пересекающиеся кривые заданы уравнениями Р(ы) и Q( ). Значение параметра, соответствующее точкам пересечения, задается уравнением

P( )-Q(*0 = 0. (6.70)

Обратите внимание, что уравнение (6.70) распадается на три скалярных уравнения с двумя неизвестными. Выберем какие-либо две компоненты векторов, например х и у:

Px( )-QAv) = 0; (6.71)

РУ(М)-0.У(Р) = Ъ. (6.72)

Решим уравнения (6.71) и (6.72) относительно и и v и воспользуемся оставшимся скалярным уравнением (компонентой г уравнения (6.70)), чтобы проверить полученные значения и к v. Системы нелинейных уравнений обычно решаются численными методами, такими как метод Ньютона-Рафсона [39]. Последний требует вычисления производных Рх, Q , Р„, Q, для чего нам потребуются выведенные в разделах 6.4.1, 6.5.3 и 6.6.2 формулы дифференцирования уравнений кривых.

Решая уравнения (6.71) и (6.72) любым численным методом, мы можем столкнуться со следующими проблемами.

□ Итерации могут разойтись, если начальные приближения и и v окажутся слишком далеки от настоящих решений.

□ При наличии нескольких точек пересечения может случиться, что не все они будут найдены. Обычно возвращается решение, находящееся ближе всего к начальному приближению.

□ Ситуация, в которой часть одной кривой точно совпадает с частью другой кривой, не может быть обработана алгоритмом в силу его внутренних особенностей. В этом случае будет возвращено неопределенное количество точек пересечения.

□ Если в некоторых местах расстояние между кривыми очень мало, координаты этих участков могут быть возвращены в качестве точек пересечения (в зависимости от внутренней погрешности алгоритма).

Первая и вторая проблемы решаются последовательным заданием начальных приближений, близких к реальным точкам пересечения. Для кривых Безье и В-сплайнов начальные приближения могут быть получены путем аппроксимации кривых отрезками. В приложении Ж мы показали, что аппроксимация кривой Безье или В-сплайна отрезками получается путем последовательного деления такой кривой. Третья проблема обычно возникает при расчете точек пересечения простых кривых, например отрезков или дуг окружностей. Например, мы можем попытаться найти численным методом точку пересечения двух дуг, лежащих на одной и той же окружности, преобразовав уравнение каждой из них к уравнению NURBS. Вспомните, что это преобразование часто выполняется для того, чтобы одна программа могла работать с кривыми любых типов. Численный метод не может обнаружить перекрытие, поэтому он возвратит неопределенное количество точек пересечения, зависящее от начального приближения. Следовательно, проверять возможность перекрытия следует до вызова численного метода. Эта проверка может осуществляться путем сравнения характерных параметров кривых, например центров и радиусов дуг, перед преобразованием их к форме NURBS. Четвертую проблему в большинстве случаев можно решить, правда не полностью, аккуратной настройкой точности численного метода.

Рассмотрим теперь более простой метод определения точки пересечения, который применим в том случае, если одна из кривых является прямой. Предположим, что Р(и) - уравнение прямой, a Q(a) - уравнение кривой. Если прямая проходит через точки, положение которых задается векторами Р0 и Р(, то ее уравнение может быть записано следующим образом:

P(w) = P, +и(Р, -Р0). (6.73)

Параметры и и v в точке пересечения должны, таким образом, удовлетворять уравнению

Р0+М(Р, -Р0) = О . (6.74)

Умножим левую и правую части уравнения (6.74) скалярно на Р0 х Р,:1

(PoxP,)-Q(D) = 0. (6.75)

Нелинейное уравнение (6.75) может быть решено относительно v численным методом. Однако здесь нас подстерегают те же проблемы, что и раньше.

1 Уравнение получается таким, потому что скалярное произведение Р0 или Pi на равно нулю.

Вопросы и задачи

1. Чтобы нарисовать эллипс, изображенный на приведенном ниже рисунке, вам придется получить выражения для координат х и у граничных точек параметрического уравнения.

У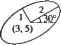

1) Получить уравнение эллипса, расположенного в начале координат и направленного таким образом, что его большая ось совпадает с осью х.

2) Применить необходимые преобразования к уравнению, полученному в предыдущем пункте, для вывода уравнения эллипса, показанного на рисунке.

Пусть эрмитова кривая, лежащая в плоскости ху, определяется следующими геометрическими коэффициентами:

Р(0)

Р(1) Р'(0)

Р'(1)

1) Найти кривую Безье третьего порядка, максимально точно соответствующую этой эрмитовой кривой. Иначе говоря, необходимо определить четыре задающие точки кривой Безье.

2) Раскрыть уравнения обеих кривых в полиномиальной форме и сравнить их.

Кривая Безье с задающими точками Ао, Ai и А2 преобразуется в кривую Безье с задающими точками В0, Bi и В2 (см. рисунок). Преобразование должно переместить точку Ао в В0 и А2 в В2. Таким образом, это преобразование должно включать в себя масштабирование.

У

В20, 2+V3)

Л](2, 3W / Кривая С2

Во(5, 2)

А>(1,1)

1) Выбрать нужные матрицы преобразования и определить порядок их применения.

2) Определить координаты задающей точки Bt.

3) Записать параметрическое уравнение кривой С2.

4. Найти кривую Безье третьего порядка, аппроксимирующую четверть окружности с центром в точке (0, 0). Концы аппроксимируемой дуги: (1, 0) и (0, 1). Найти координаты середины кривой Безье и сравнить их с координатами середины дуги.

5. Изучите кривые Безье, изображенные на рисунке. Кривую 2 необходимо присоединить к кривой 1, переместив точку D к точке С. Нужно также обеспечить непрерывность первой производной в точке соединения. Какими будут задающие точки объединенной кривой?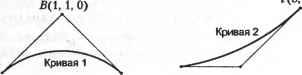

Аф, 0,0) С(2,0,0) £>(3,0,0) £(4,0,0)

6. Непериодический В-сплайн четвертого порядка определен четырьмя задающими точками:

Р„ =(0,0,0);Р, =(6,8,0); Р2 =(12,8,0>,Р3 =(18,0,0). Что получится, если повернуть эту кривую вокруг оси х на 180°? Если это будет В-сплайн, то каким будет его порядок и какие у него будут задающие точки?

7. Непериодический В-сплайн третьего порядка определен задающими точками Ро, Р Р2, Рз-

1) Какими будут узловые значения параметра?

2) Из скольки различных кривых состоит В-сплайн?

3) Раскройте уравнение В-сплайна и получите уравнения кривых из предыдущего пункта.

8. Представить окружность единичного радиуса с центром в начале координат кривой NURBS с семью задающими точками (см. рисунок). Вам нужно получить порядок кривой к, узловые значения параметра и однородные координаты задающих точек (х -w,y -w, z-w, w).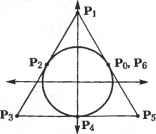

9. Интерполируйте точки Po(0, 0), Pi(l, 2), Рг(3, 2) двумя эрмитовыми кривыми Pi(w) и Рг(и). Считайте, что в точках Ро и Р2 концы кривой не закреплены.

10. С помощью любой доступной вам системы автоматизированного проектирования продемонстрируйте:

О глобальность изменений для кубических сплайнов и кривых Безье; О локальность изменений для В-сплайнов; О выпуклость оболочки кривых Безье;

О влияние дублирования задающих точек на кривые Безье и В-сплайны.

11. Напишите программу с перечисленными ниже меню и функциями.

О Меню ввода задающих точек: позволяет пользователям вводить координаты задающих точек непериодического В-сплайна третьего порядка на плоскости ху. Максимальное количество задающих точек - 10. Задание точек производится маркером, который устанавливается мышью в нужное место, после чего следует нажатие на кнопку мыши (то есть мышь используется в режиме опроса).

О Окончание ввода: выбирается пользователем после указания всех задающих точек. При выборе этого пункта программа должна вывести на экран В-сллайн и задающий многоугольник.

О Меню изменения задающих точек: позволяет пользователю изменять положение задающих точек (по одной). Пользователь должен иметь возможность выбрать любую задающую точку и перетащить ее в новое место. В процессе перетаскивания система должна динамически перестраивать новый В-сплайн вместе с задающим многоугольником. О Меню удаления: это меню позволяет пользователю удалять В-сплайн

щелчком на любом ребре соответствующего задающего многоугольника. О Выход: этот пункт меню завершает работу с программой.

Глава 7

Представление поверхностей и работа с ними

Системам геометрического моделирования приходится хранить уравнения кривых (или эквивалентные характеристические параметры) для всех ребер и уравнения поверхностей (или эквивалентные параметры) для всех граней. Полезно знать, какими бывают уравнения поверхностей и какими параметрами они характеризуются. Мы говорили, что для реализации булевских операций необходимо рассчитывать точки пересечения кривых. В системах поверхностного моделирования с той же целью приходится определять кривые, по которым пересекаются поверхности. Например, если поверхность в процессе моделирования отсекается другой поверхностью, это требует вычисления кривой, по которой они пересекаются. Эта задача требует вычисления координат точек на поверхностях, а также производных в этих точках. В настоящей главе мы коротко рассмотрим различные типы уравнений поверхностей и методы работы с ними: методы вычисления координат, дифференцирования и обработки пересечений. Все эти вопросы рассматриваются более подробно в книгах по вычислительной геометрии [9, 49, 48, 129, 72, 112].

7.1. Типы уравнений поверхностей

Уравнения поверхностей, как и уравнения кривых, делятся на два основных типа. К первому типу относятся параметрические уравнения, связывающие значения координат х, у и z со значениями параметра. Ко второму относятся непараметрические уравнения, связывающие координаты х, у и z непосредственно друг с другом какой-либо функцией. Поясним эти определения на простом примере. Рассмотрим сферу радиуса R с центром в начале координат. Параметрическое уравнение этой сферы будет иметь вид:

P(u,v) = Rcosu cosv i + Rsinu cosv j + Rsmv k;

(0 <u <2n,-n/2 <v <n/2), где параметр и может рассматриваться как долгота, a v - как широта. Ту же сферу можно описать и без параметров и и v:

или

х2 +у2 +z2 -R2 = 0

(7.2)

Уравнение (7.2) называется неявным пепараметрическим, а уравнение (7.3) - явным непараметрическим.

У каждого типа уравнений есть свои преимущества и недостатки, но мы будем рассматривать только параметрические уравнения. Как отмечалось в главе 6, параметрическое уравнение позволяет эффективно вычислять точки на поверхности или кривой, отстоящие друг от друга на небольшие расстояния, что облегчает интерактивное отображение объекта и работу с ним. Это одна из главных причин, по которым параметрические уравнения используются для представления поверхностей в большинстве систем автоматизированного проектирования1.

7.2. Билинейная поверхность

Билинейная поверхность (bilinear surface) строится по четырем заданным точкам и описывается линейными уравнениями с параметрами и и v. Эти точки оказываются в углах построенной поверхности. Мы обозначим их буквами Р0 0, Pi.o, P<u> рм (Рис- 7.1). Вывести уравнение билинейной поверхности - это значит найти выражение для координат произвольной точки по значениям параметров и и v. Предположим, что эта точка делит отрезок [Ро. ,?! , ] в отношении и:(\ - и) (рис. 7.1). Точки Р0г и Р|Л, делят отрезки Р00Р0, и Pli0Plfl соответственно в отношении v:(\ - v). Определенная таким образом точка P(u.v) будет перемещаться по всей поверхности при изменении параметров и и а от 0 до 1. С учетом сделанных предположений координаты точек Р0(, иР( запишутся следующим образом:

Р0, = (l-v)Pop+vPol; (7.4)

Ptv=(l-v)Pl0+vPu. (7.5)

Pi,i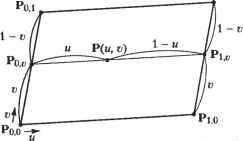

Рис. 7.1. Билинейная поверхность и ее опорные точки

Кривые, по которым пересекаются поверхности, в некоторых случаях бывает удобно рассчитывать, представляя одну из этих поверхностей параметрическим уравнением, а другую - непараметрическим. Поэтому в некоторых системах могут использоваться и непараметрическпе уравнения поверхностей, хотя и не как основной тин уравнений для хранения сведений о кривых. В этом случае возникает потребность в процедуре преобразования из параметрической формы в непараметрическую и обратно. Такое преобразование рассматривается в работе [69].

Аналогичным образом получаются координаты точки P(u,v):

P(u,v) = (i-u)P0v+uPu,. (7.6)

Подстановка уравнений (7.4) и (7.5) в (7.6) даст нам приведенное ниже уравнение билинейной поверхности:

P(u,v) = (\-u)[(\-v)Pw +vP0A] + u[(\-v)Plf) +vPu] =

= [(1-m)(1-i0 u(l-v) (i-u)v uv\

P.,o Po,

p...

(0<u < 1,0 < £!).

(7.7)

Мы можем убедиться, что заданные точки расположены по углам билинейной поверхности, подставив соответствующие комбинации нулей и единиц в уравнение (7.7). Это уравнение говорит нам также о том, что билинейная поверхность представляет собой сопряжение угловых точек при помощи функций сопряжения (1 - ы)(1 - v), и(1 - ), (1 - u)v, uv. Из-за того что эти функции сопряжения линейны по соответствующим параметрам, билинейная поверхность обычно оказывается плоской.

7.3. Лоскут Куна

Сопряжение углов дает билинейную поверхность. Сопряжение граничных кривых произвольной формы дает поверхность, называемую лоскутом Куна (Coons patch). Слово лоскут указывает на то, что описываемая поверхность представляет собой сегмент, соответствующий значениям параметров 0 < ы < 1, 0 < о < 1. Комбинирование лоскутов позволяет образовать поверхность произвольной формы и размера.

Уравнение лоскута Куна выводится следующим образом. Предположим, что нам известны уравнения четырех граничных кривых: P0(v), Р, (v), Q0(w) и Q,(w) (рис. 7.2). Предположим также, что направление кривых Q0(u) И Q, (и) совпадает (на рис. 7.2 эти кривые направлены вправо, что обозначено стрелкой). То же предположение мы выскажем и относительно P0(v) и Р, (v).

Qi( )

Pi(f)

и Qfl(K)

Рис. 7.2. Граничные кривые, определяющие лоскут Куна

Если граничные кривые не удовлетворяют этим требованиям, вам придется выполнить преобразование их к описанному выше виду. Направление и интервал изменения параметра легко изменить инверсией или масштабированием [120].

Удовлетворяющие описанным требованиям кривые интерполируются так, как показано ниже.

Выберем две кривые, расположенные друг напротив друга, например P0(v) и P,(rj). Интерполяция этих кривых в направлении и осуществляется линейным уравнением

Pl(u,v) = (i-u)P0(v) + uPl(v). (7.8)

Поверхность, определенная уравнением (7.8), будет ограничена кривой Р0 (v) при и = 0 и кривой Р, (v) при и = 1. Однако две другие границы будут отрезками прямых, соединяющих угловые точки. Убедиться в этом можно, подставив в уравнение (7.8) v = 0 или о=1. Таким образом, полученная поверхность не ограничивается кривыми QoQ., (и).

Определим вторую поверхность, интерполируя Q0(u) и Q0(a) в направлении v.

P2(u,v) = (l-v)Q0(u) + vQ,(u). (7-9)

Подставляя граничные значения и и v в уравнение (7.9), можно убедиться, что новая поверхность ограничивается кривыми Q0(u) и Q0(a), но не P0(v) или Р, (р). Попробуем определить еще одну поверхность Р3 (u, v), сложив Р, (и, v) и P2(u,v), и проверим, не будет ли она ограничиваться требуемыми кривыми.

Р3 (u,v) = (1 -и)Р0 (v) + и Р, (v) + (1 -v)Q0(u) + vQ, (и). (7.10) Подстановка граничных значений и и v в (7.10) дает:

Р3(0,о) = Р0(о) + (1 -o)Q0(0)+oQ, (0); (7.11)

P3(i,v) = Р, (v) + (1 - )Q (1) + vQ{ (1); (7.12)

Р3 ( .0) = Qo( ) + (1 - и)Р„(0) + и Р, (0); (7.13)

P3( ,l) = Q,( ) + (l- )Po(l) + Pi(l)- (7-14)

Если P3(u,v) удовлетворяет поставленным требованиям к граничным кривым, правые два слагаемых в уравнениях (7.11)-(7.14) должны быть равны нулю. Заметьте, что эти слагаемые представляют собой интерполяцию конечных точек соответствующих граничных кривых. Другими словами, слагаемые, которые должны быть равны нулю, описывают границы билинейной поверхности. Следовательно, правильное выражение для лоскута Куна получается вычитанием уравнения билинейной поверхности из P3(u,v):

P(u,v) = (1 -и)Р0(о) + uPt(v) + (1 -v)Q0(u) + vQt (u)-(l-u)(\-v)P - (7 l5) -u(\-v)Pl0-(\-u)vP0A-uvPu (0<u<i, 0uv<l).

Здесь P0.o=Po(0)=Qo(0),P,.o =Qo(l)=P.(0),Po., =P0(l)=Q.(0).p... =P,0)=Q.(1)-

Благодаря простоте концепции и уравнений лоскут Куна использовался достаточно широко. Однако он непригоден для точного моделирования поверхностей, поскольку форма поверхности не может задаваться одними лишь ее границами.

7.4. Бикубический лоскут

Бикубический лоскут (bicubic patch) - это поверхность, определяемая полиномиальным уравнением третьего порядка по параметрам и и V.

P(u,v) = X J a,vuV (0 < u < 1, 0 < v < 1). (7.16)

Уравнение (7.16) можно переписать в матричной форме:

P(u,v) = [l и и'

00 01

а,0 о.

02 03

12 13

20 21 22 23

(7.17)

В уравнениях (7.17) - алгебраические векторные коэффициенты с компонентами д:,уиг. Влияние этих коэффициентов на форму поверхности не является интуитивно понятным, точно так же, как по алгебраическим коэффициентам уравнения (6.10) нельзя было представить себе форму кривой. Возникает желание заменить алгебраические коэффициенты на геометрические, что было сделано ранее при выводе эрмитовой кривой. Поскольку алгебраических коэффициентов для поверхности насчитывается 16 штук, нам нужно ввести 16 граничных условий.

Первый набор граничных условий мы получим, потребовав, чтобы четыре граничные точки Р(0,0),Р(0,Г),Р(1,0),Р(1,Г) удовлетворяли уравнению (7.17). Чтобы получить второй набор граничных условий, мы зададим векторы касательных к граничным кривым поверхности в угловых точках по параметрам иикР, (0,0), Рн(0,1), Ри(1,0), Рв(1,1) и РД0.0), Рц(0,1), РД1.0), РД1.1). Перечисленные граничные условия определяют форму граничных кривых поверхности, поскольку они определяют конечные точки этих кривых и векторы касательных в этих точках. Через заданные граничные кривые можно провести бесконечно много поверхностей, поэтому нам придется добавить граничные условия, которые определяли бы форму внутренней области поверхности. Мы потребуем, чтобы вторая производная в угловых точках имела определенные значения Риг,(0,0), Рив(0,1), Рк!,(1,0), PO.l). Под второй производной мы понимаем следующее выражение, называемое вектором кручения (twist vector):

d2P(u,v)

ди dv

Ниже мы обсудим влияние векторов кручения в угловых точках на форму внутренней области поверхности.

Подстановка 16 граничных условий в уравнение (7.17) даст нам 16 линейных по а.- уравнений. Эти уравнения образуют систему, результат решения которой подставляется обратно в уравнение (7.17), что дает нам приведенное ниже уравнение бикубического лоскута:

Уравнение эрмитовой кривой получается при помощи аналогичной процедуры.

P(u,v)-

I I

= [F[(u) F2(u) Fa(u) Ft(u)]

F2(v)

(7.18)

(7.19)

P(0.0) P(0,1) P,.(0,0) P (0,1) P(1,0) P(l,l) РД1.0) РД1.1) P (0,0) P.(1,0) P (0,0) PM.(0,1) P (1,0) P (l,l) P (1,0) PM,(1,1)

(0<w <1,0<в<1), где функции сопряжения Ft, F2, F3 и F4 определяются следующим образом:

F,(u) = 1-3m2 +2ы3; F2(u) = 3u2 -2u3; F3(u) = u-2u2 +u3; РЛ(и) = -и2 +u3.

Это те же функции сопряжения, что и в уравнении эрмитовой кривой. Вообще говоря, уравнение (7.18) представляет собой попросту расширение уравнения эрмитовой кривой для описания поверхности. Уравнение (7.18) может быть редуцировано до уравнения кривой путем подстановки конкретного значения одного из параметров, например!) =г0. Произведение последних двух матриц в правой части уравнения (7.18) дает вектор-столбец. Это умножение может быть интерпретировано следующим образом. Первая строка дает уравнение левой граничной кривой между Р(0,0) и Р(0,1), а вторая строка дает уравнение правой граничной кривой между Р(1,0) и Р(1,1) (рис. 7.3). При подстановке конкретного значения v0 первые две строки дают нам конечные точки А и В. Последние две строки столбца для v = и0 задают векторы касательных в направлении и в точках А и В. Последнее утверждение мы проверим позже. Следовательно, уравнение (7.18) представляет собой объединение уравнений эрмитовых кривых, соответствующих разным значениям v. Граничные кривые, определяемые условиями v = 0 и v = 1, будут эрмитовыми кривыми. Аналогичным образом можно показать, что и граничные кривые для и = 0, и - 1 тоже будут эрмитовыми.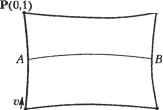

Р(о,оуг P(i,o)

Рис. 7.3. Изопараметрическая кривая v = v0

При попытке воспользоваться уравнением (7.18) мы столкнемся с проблемой задания векторов кручения, влияние которых на форму поверхности не является интуитивно понятным. Иногда для простоты им присваивают нулевые значения. Получаемая таким способом поверхность называется лоскутом Фергюсона или F-лоскутом (Fergusons patch или F-patch). Поскольку нулевые векторы кручения