Алгоритм 4.9. Программа на Pascal\решения задачи Счастливый билет Program Lucky ticket; {Счастливый билет uses CRT, DOS; Const

max n=20; Type

Vector=array [1. .max n] of Longlnt;

Procedure ( var ; var a , b : Vector ;

n, m:Integer ) ;

S : Longlnt;

i : Integer; begin

S:=a[l];

for i:=l to n-1 do S:-S + (2*b[i]-l) *a[i + l] ; if S=m then begin Write(f, a[1]) ; for i:=l to n-1 do begin

if b[i]=l then Write (f,+) else Write (f,-); Write (f,a[i + l]) ; end;

WriteLn(f, = \S:4, - число найдено!);

end; end;

Procedure var var

n,m: Integer ) ;

b: Vector; i : Integer;

begin

for i:=l to n do b[i]:=0; while b[n]ol do begin Summa(f,a,b,n,m); i: =1 ;

while b[i]=l do begin

b[i]:=0;

i:=1+1; end;

b[i]:=1; end; end;

Var {Main}

a :Vector;

n,m, i :Integer; f :Text; {Текстовый файл)

Hour,Minute,Second, SeclOO :Word; rHour,rMinute,rSecond, rSeclOO :Word; delta rLonglnt; begin(Main)

Assign(f,Number.in); Reset (f);{Файл открыт для чтения) Read(f.n); {Ввог количества цифр) Read(f,m); {Ввод счастливой суммы) for i:=l to n do Read(f,a[i]); Close(f);

Assign(f, Number.out)

Rewrite (f5; (Фай/ открыт для записи) GetTime(Hour,Minute,Second,SeclOO) ; SubSet(f,a,n,m);

GetTime(rHour,rMinute,rSecond,rSeclOO);

delta:-rHour-Hour; delta:-delta*6 0 + rMirmte-Minute;

delta:=delta*60+rSecond-Second;

delta:=delta*100+rSeclOO-Secl00;

WriteLn(f); WriteLn(f,Время счета=,

delta div 100, , ,delta mod 100, c ) ; Close (f); end{Main}.

4.5. Генерация размещений с повторениями

Порождение множества всех размещений с повторениями длины к из элементов {я0, ал,. , ап {) эквивалентно генерации множества /-разрядных чисел в системе счисления с основанием и: на г-м месте в размещении будет располагаться элемент а:. если цифра в разряде соответствующего числа равна Всего размещений с повторениями п . Например, для к= 2 и п = 3 все наборы длины два в системе счисления с основанием три можно записать: 00, 01, 02, 10, 11, 12. 20, 21, 22. Тогда эквивалентные размещения примут вид

(аоя0), (fl0fli), (а0а2), (а^), (а^), (а{а2), (а2а0), (а2ах), (а2а2).

Алгоритм 4.10 использует фиктивный элемент при порождении наборов длины к в системе счисления с основанием и, где

bpiQ, 1,..., п 1},/ = О, 1,..., к, т.е. - это цифры генерируемого числа в системе счисления с основанием п.

Алгоритм 4.10. Счет в системе счисления с основанием п для порождения всех к-разрядных наборов

for / = 0 to к do bj = 0;

Print{bk vbk 2, ..,b0), /=0;

С

whilebj =n-ldo .

l -* tI;

6; =6, +1.

while 1 do

4.6. Порождение сочетаний

Обычно требуются не все подмножества множества {alt а ...., ап}, а только те, которые удовлетворяют некоторым ограничениям. Особый интерес представляют подмножества фиксированной длины к, С* сочетаний из п предметов по А: штук. Как обычно,

предполагаем, что основным множеством является множество натуральных чисел {1, 2,..., и}; таким образом, будем порождать все сочетания длины киз целых чисел {1, 2,..., л}. Так, например, С\ =20 сочетаний из шести предметов по три (т.е. трехэлементные подмножества множества записываются в лексиког-

рафическом порядке следующим образом:

123 135 234 256

124 136 235 345

125 145 236 346

126 146 245 356 134 156 246 456

Сочетания в лексикографическом порядке можно порождать последовательно простым способом. Начиная с сочетания {1, следующее сочетание находится просмотром текущего сочетания справа налево с чтобы определить место самого правого элемента, который еще не достиг своего максимального значения. Этот элемент увеличивается на единицу, и всем элементам справа от него присваиваются новые возможные наименьшие значения, как показано в алгоритме 4.11. Алгоритм порождения всех сочетаний линеен, его сложность

Алгоритм 4.11. Порождение сочетаний

со = -1;

for i = 0 to k do = i;

Print{ci,c2,...,ch)\ j=k;

whilej * 0 doi while Cj = n-k +jdo j =j -1;

Cj =Cj +1;

for i = j + \to к do Cj =c, , +L

Задача. Выпуклый многоугольник. Дано множество пар целых чисел (хуУу), (х2,у2),..., (х„,у„) - координаты точек на плоскости. Написать программу выделения тех точек из заданного множества, которые являются вершинами выпуклого многоугольника, содержащего все остальные точки. Исходные данные представлены в текстовом файле, имеющем следующую структуру. Первым числом в файле является целое л - количество точек. Последующие числа определяют п пар целых (х, у.) - координаты точек. Результаты расчетов, признаки принадлежности исходных точек выпуклому многоугольнику: 0 - точка не принадлежит, 1 - точка принадлежит, сохранить в текстовом файле.

Пример файла исходных данных:

0099512327 11 5467 15673457788764 Выходной файл для данного примера:

1 1 1 0 1 0 0 0 1 0 0 0 0 1 0

Решение. Если не применять специальных методов, то в качестве решения можно использовать следующий алгоритм. Ясно, что точка является вершиной выпуклого многоугольника, если она не лежит ни в одном вершинами которых

являются исходные точки {х^уу), (х2,у2),..., (хп,уп), без рассматриваемой точки (X/У,). Всего треугольников из п точек можно составить С„3 + 0{пг). Тогда сложность задачи полного перебора

угольников для каждой точки (Х/У,) составит 0(п). Реализация данного подхода представлена программой на языке Pascal в алгоритме 4.12.

Алгоритм 4,12. Программа поиска точек выпуклой оболочки

Program 5tart Envelope; iВыпуклая оболочка} uses CRT,DOS; const n max=100;

type Vector-array[I..n max] of Integer; Combine=array[0..3] of Integer;

var f :Text; [Текстовый файл)

x,y :Vector; {Координаты точек}

z :Vector; {Характеристический вектор выпуклой оболочки }

Procedure Envelope( var с:Combine; n:Integer );

{Формирование оболочки}

Const k :Integer-3; Var

i, a :Integer;

kl,k2,k3 :Integer;

signl,sign2,sign3 :Integer;

begin

kl: -t/lVj ; Se.-C(2.j*, r?.y;=<T rfVj ; for i:=l to n do begin

if (i=kl) or (i = k2) or (i=k3) then continue; a:=(x[kl]-x[i])*(y[k2]-y[i] )-[x[k2]-x[i])*(y[kl]-y[i]); if a=0 then continue; signl =a div abs (a); a:=(x[k2]-x[i])*(y[k3]-y[i])-(x[k3]-x[i])*(y[k2]-y[i]); if a=0 then continue; sign2 : ==a div abs (a) ; a: = (x[k3]-x[i])My[kl]-y[i])-[x[kl]-x[i])*(y[k3]-y[i])t if a=0 then continue; sign3:=a div abs (a); if (signl=sign2) and (sign2 = sign3) then z[i]:=0; end; end;

Procedure var

Var i : Integer;

begin

WriteLn(f);

for i:=l to n do

end;

Procedure Combination( n:Integer );

{Генерация сочетаний из п по Const k :Integer=3; {Длина сочетания} Var с :Combine; {Сочетание} i,j . Integer;

begin

for i:=l to к do c[i]:=i;

j:=l;

while j<>0 do begin {Print(с,k);} Envelope(c,n) ; j:=k;

while c[j]=n-k+j do j:=j-l; c[j]:=c[j]+l;

for i:=j+l to k do c[i]:=c[i-l]+l; end; end;

Var {Main)

i,n :Integer; {Числе исходных точек) begin {Main}

Assign(f, Envelope.in);

Reset(f); {Файх открыт для чтения)

Read(f,n); {Ввод данных}

for i:=l to n do begin Read(f,x[i],у[il); zfi):=l;end; Close(f);

Assign(f,Envelope.out);

Rewrite(f); {Фай* открыт для записи}

Combination(n);

WriteLn(f); {Результаты: номера точек выпуклой оболочки} for i:=l to n do Write(f,z[i], v) ; Close(f); end. {Main}

4.7. Порождение композиций и разбиений

Рассмотрим задачу порождения разбиений положительного числа п в последовательность неотрицательных целых чисел fci, z2,..., Ьтакчтоггг ... +3f п.

Разбиение {ц, zb..., zk) называется композицией числа п, если учитывается порядок чисел zr Как правило, представляют интерес композиции, в которых либо все щ > 0, либо все Zj > 0.

Разбиение {ц, z2,-, Zk) назътштсяразбиением числа п, если все Zi>0 и порядок чисел Z, не важен. По сути разбиение {Z\, Z2,---, Z/J числа я является мультимножеством (см. п. 1.8).

Рассмотрим примеры разбиения числа п = 3. (1, 2), (2, 1) - все композиции числа три из двух частей, > 0. (1, 1, 1) - все композиции числа три из трех частей, > 0. (О, 3), (1, 2), (2, 1), (3, 0) - все композиции числа три из двух частей, z, > 0.

(3), (1, 2), (1, 1, 1) - все разбиения числа три.

Композиции О

Композицию {zi, z2,...,zk), гдег,> 0, числа^ +Z2 +-+zk = п можно интерпретировать следующим образом. Каждое значение г,- = 1, + 1,+ ... + 1/ представим как сумму единиц, количество которых Zj- Индекс у элемента 1, показывает его принадлежность разложению числа Zj. Таким образом, мы ввели к типов различных элементов {1[, 12, .., 1д}, значение каждого из них равно единице. Теперь любую композицию можно представить как сумму, составленную из п произвольных единиц множества {\ь \2,..., \к). Суммируя подобные единицы 1;с одинаковыми индексами, получим соответствующие значения z, композиции. Данное соответствие является взаимно однозначным, откуда и следует, что число композиций равно числу сочетаний с повторениями С\ = C*~J j = C+k t. Каждое из сочетаний С^, можно интерпретировать как расстановку 1 и О

длины п + к - в которой п единиц и к - 1 нуль, т.е. каждому сочетанию ставим в соответствие (п + к - 1)-разрядное число из единиц и нулей; верно и обратное. Суммируя в таком числе слева направо единицы между нулями (их к - 1), будем получать соответствующие значения членов Z\ (их к) композиции. Например, одному из Сп+к-1 =С117+7-1 сочетаний 11011100111101111111010 соответствует композиция (2,3,0,4,7,1,0) числа 17.

Ясно, что методы предыдущего раздела генерации подмножеств множества легко применить к последовательному порождению рассмотренных композиций 0.

Композиции > О

Удобное представление композиций получается из рассмотрения целого числа п как отрезка прямой, состоящего из отрезков единичной длины. Линия разделена п - 1 точками, и композиция

ч--2-- - 1 - --2---2-* +- I

--®- 0- -®-- --®-

получается пометкой некоторых из них. Элементами композиции являются просто расстояния между смежными точками. На рисунке показано графическое представление композиции (2,1,2,2,1) для числа п = 8. Очевидно, что каждая композиция числа соответствует способу выбора подмножества из п - 1 точек. Каждой точке можно сопоставить двоичную цифру, и, таким образом, композиции п будет соответствовать (п - 1)-разрядное число. В этой интерпретации композиция из к частей соответствует^ - 1)-разрядномучислу ровно с к - 1 единицами, и поэтому существует Скп~ { таких композиций.

Воспользуемся методами предыдущего раздела для генерации композиций щ> 0. Учитывая, что в композиции z\ + % +... + Щ = и каждый из > 0, тогда для новых переменных = - 1,(г, > 0) соответствующая композиция будет для числа = = г\ + г2 +--+ гь гт О-Генерация слагаемых /*; Ю композиции (г\, гъ..., гк) подробно разобрана в предыдущем разделе, добавляя к каждому из по единице, получим слагаемые 0 композиции {Z\,Z2, - , Zk}-

Разбиения

Разбиения п отличаются от композиций п тем, что порядок компонент не важен, так что, например, не делается различия между, скажем, 1+1+2, 1+2+1,2+1+1. Таким образом, разбиение п можно рассматривать как которое записы-

вается следующим способом:

{Wj zi,m2 z1,...,mk zk},

где имеется вхождений z\, вхождений z- >Щ вхождений

к

и т. д. ии = л,г|. Каждое разбиение удовлетворяет условию

> > ... > Рассмотрим пример генерации разбиений для п = 7. Последовательность генерации разбиений данного примера далее будет положена в основу алгоритма порождения полного

списка разбиений.

Идея приведенного списка разбиений состоит в том, чтобы переходить от одного разбиения к следующему, рассматривая самый правый элемент mк zk разбиения. Если достаточно ве-

лико (т.. > 1), можно исключить два для того, чтобы добавить еще одно zk + 1 (или включить одно zk 1, если в текущий момент его нет). Если тк= \, то mk izk-i + mkzk достаточно велико для того, чтобы добавить Zk-\ + 1. Все, что остается, превращается в соответствующее число единиц и формируется новое разбиение.

Алгоритм использует рассмотренный процесс для порождения всех разбиений числа п.

Алгоритм 4.13. Генерация разбиений числа п

к= 1;

г д = 0; т ! =0; Ц = п+ 1;

Z\ = 1;

Print{ml zvm1 z1,...,mk*zk); Summa = mhzk;

while k 0 do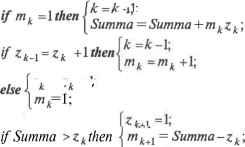

[k=k+l

Алгоритм 4.13 линеен, так как число операций, необходимых для перехода от одного разбиения к другому, ограничено константой, не зависящей от п и к.

Программа на языке Pascal реализации рассмотренного метода генерации разбиений чисел приводится в алгоритме Отметим, что в программе число для разбиения п читается из файла, а порождаемые разбиения сохраняются в файле. Попутно программа вычисляет полное время генерации всех разбиений с точностью до сотых долей секунды, которое сохраняется в конце

файла сгенерированных разбиений.

Алгоритм 4.14. Программа на Pascalе генерации разбиений

числа п

Program Start Divide; {Разбиение числа

uses CRT,DOS; Const

max n=100; { n<=max n }

Type

Vector=array[-l..max n] of Integer; Var

f :Text; z,m :Vector;

Procedure var k: Integer );

(Печать разбиения}

i :Integer; begin

Write (f, {) ; for i:=l to k do begin Write(f,m[i],*,z [i]) ; if iok then Write (f ) ; end;

Writel.n (i, } ); end; {Print}

Procedure числа

k, Sum :Integer; begin; k:=l; z[-l]:=0; m[-l]:=0;