части (3.5.1) одинаковый. Пусть j е 5 обладает точно /свойствами. Возможны следующие соотношения между / и т:

1) / < т, тогда не входит в Е(т) и не входит в -И) для /=0, 1,...,л - т. Равенство (3.5.1) приметвид 0 = 0.

2) / = т, тогда (s, входит один раз в и один раз в W(m).

3)/>т, тогда и (У не входит в Е(т) и левая часть равна 0. Покажем, что в этом случае и правая часть выражения (3.5.1) равна нулю.

Вес co(s) в Щт + i) входит С,ш+/ раз, т + К/. Правая часть для веса со (s) одного элемента s примет вид

(%фус? -с^1ф)сг1+..М-1)-тс?ф)С1 ь

= Ш(.)£(-1)С+,СГ.

Заметим, что

Ст m+i (/я+/)! t\ /! (t-m)!

да!/! (m+i)\(t-(m+i))\ m\(t-т)\ i\((t-m)-i)\

Следовательно, CC = €?€} , а исходная сумма составит

t-m t-m

=<Ф)сг5н>с;-т uijcrd-i)- =о.

/=о

И в третьем случае выражение справедливо. Теорема дока-

Следствие.

Е(0) = Щ0) - W(2) - ЩЩ + ... +(-1) Щп).

Задача. В группе 23 студента. Из них 18 знают английский язык, 9 - немецкий и 6 - оба языка. Сколько студентов в группе не знают ни одного языка? Сколько студентов знают один язык?

Решение. Пусть S-множество всех студентов, \S\ =23. Назначим вес со($) = 1 всем элементам s s S. Теперь под суммой весов будем понимать количество студентов.

Назначим свойства элементам s е S: Р\ - знание английского языка, - знание немецкого языка. ДО) - студенты, не знающие языков (не обладают свойствами).

£(0) = W(0} - W(\) + W(2). (0)=£>(5> = 23.

W{\) =W(P. + W(P2 = 18 + 9 = 27. WQ\ = W{P{P2 )= 6. Тогда E(0) = 23 - 27 + 6 = 2.

Е( 1) - студенты со знанием одного языка (обладают ровно одним свойством).

£a)=Ci1a)-Ci(2)=ia8+9)-2 6=15.

Задача. Найти число перестановок т шаров, в которых ровно г шаров остаются на месте.

Решение. Введем обозначения. Pt - свойство, состоящее в том, что при перестановке шаров шар остается на месте, = 1, т. Е(г\ - количество перестановок, обладающих ровно г свойствами, т.е. при перестановке шаров ровно из них остаются на своих местах. Тогда по формуле включений и исключений запишем:

Е(г) = (-1) Cr+IW(r + i). Рассмотрим W(r)= £ Щ^Р, г... P,f),

где суммирование выполняется по всем сочетаниям (i*2****r) длины г из т свойств, количество сочетаний равно Сгт. W (PjPj 2 .Pir)= (m-r)\ - количество перестановок из т - шаров, так как г шаров должны оставаться на месте. Тогда значение

т-г

W(r) = Сгт(т --Следовательно, и Е(г) = £(-])Crr+iCrm+i(т -г-/)!

, . т\е-1 или Е(г) = - Ут-- ~--

3.6. Ладейные многочлены и многочлены

попаданий

Основная цель данного подраздела - показать возможности применения методов подсчета и оценивания при решении конкретных задач. В то же время обсуждаемые здесь задачи сами по себе не лишены интереса, и в большей степени для тех, кто впервые знакомится ними.

.] .л

3.6.1. Ладейные многочлены

Определение. Доской запрещенных позиций называется произвольный набор выделенных клеток шахматной доски, сохраняющих свое расположение относительно других клеток доски. Пример доски запрещенных позицтлй показан на рис. 3.1. Рис. 3.1

Определение. Пусть С - доска запрещенных позиций. Введем обозначения: гк - количество способов расставить к ладей на доске запрещенных позиций так, чтобы они не били друг друга; /*о = 1 - количество способов расстановки О ладей на доске запрещенных позиций, т.е. способов не ставить ладьи на доску. Ладьи считаются неразличимыми. Производящую функцию последовательности {гк} будем называть ладейным многочленом доски С и обозначать

Дх,С) =Yjk-k- (3.6.1)

щ Задача. Найти ладейный многочлен для доски

: > на рис. 3.2. Рис. 3.2 Решение. Непосредственным подсчетом можно установить, что r = 1, п = 1 и г, = 0, / > 2. Тогда Щх, ф = 1 +х.

Задача. Найти ладейный многочлен доски на рис. 3.3.

Решение. Непосредственным подсчетом можно установить, что г0 = 1, Г\ = 2, r2 = 1 и ц = О, i > 3. Тогда R(x, С2) = 1 + 2х + х2.

Задача. Найти ладейный многочлен доски на

ЩЩ рис. 3.4.

Рис. 3.4 Решение. Непосредственным подсчетом можно установить, что r0 = 1, гх = 3, r2 = 1 и г,- = 0, / > 3. Тогда R(x, С3)= 1 + ЗХ + Х2.

Определение. Доски и называются независимыми, если их клетки располагаются на различных горизонталях и вертикалях. Пример независимых досок показан на рис. 3.5.

Рис. 3.5

Свойства ладейных многочленов

Свойство 1. Правило произведения. Пусть R(x, Су) и R(x, С2) -ладейные многочлены независимых досок С, и С2. Если доска С=С,и С2, то R(x, С) = R(x, Cy)R(x, С2).

Доказательство. Пусть щ - расстановка ладей на доске Сь п2 - расстановка ладей на доске CV Тогда тс = (Л[, я2) - перестановка ладей на доске С = С, и С2. Верно и обратное. Пусть S и

SKi - множество расстановок лад ей надоске, соответственно Cj и С2. Тогда прямое произведение - множество рас-

становок ладей на доске С.

Обозначим веса расстановок: со(.п1) =х', где - число ладей в

перестановкеку;о(к2) =xkl, гдек2 - число ладей в перестановке л2.

к +к к к

Тогда вес перестановки равент(я) = х1 1 =х 1-х 2 = ы(л, )gj(ti2 ).

В соответствии с тем, как введены веса перестановок, ладейные многочлены можно записать как сумму весов элементов множеств:

R(x,Cl)= ю(я1), Я(х,С2) = 2]со(л2) и R(x,C) = со(я).

Многочлены R(x, Су), Я(х, С2) и R{x, С) удовлетворяют всем условиям правила обобщенного произведения (см. п. 3.4), в соответствии с которым R(x, С) = R(x, Cy)R(x, С2).

Задача. Найти ладейный многочлен доски С на рис. 3.6.

Пусть Су - доска из одной клетки, 1

R(x, Cj) 1 х. Ясно, что доска С состоит из л L

независимых досок Су. Отсюда следует, что Г

R(x,Q=[R(x,Cl)}n = (\+xy. ~ ;

Свойство 2. Правило суммы. Пусть С - доска РИС. 3.6 запрещенных позиций. Введем обозначения:

- доска с ладьей в клетке а ! / - index); Cf - доска с удаленной клеткой а (е - rase). Тогда R(x,C) = xR(x,CL)+R(x,C)a или R(xia + ea) = xR(ia)+R(ea ).

Для доказательства данного свойства вновь рассмотрим ладейный многочлен как сумму весов перестановок. Все расстановки множества разобьем на два подмножества SXl и Sn . SK -перестановки с ладьей на клетке а; 5 - перестановки, которые не

занимают клетку ос.

Тогда

Множитель х перед скобкой - это вес ладьи в перестановке щ которая поставлена на выделенную клетку а. Задача. Найти R(x, С) для доски на рис. 3.7.

Решение. Воспользуемся правилом суммы, по которому

R{x, Q=x- ДГЭ + Ш ) = х(1 н 4 = 1 + [х+Тд+х3.

Рис. 3.7

Отметим, что по виду полученного ладейного многочлена (производящей функции) можно сказать, что число способов расставить две ладьи на доску С равно 4.

Свойство 3 для прямоугольных досок. Пусть С - прямоугольная доска запрещенных позиций размером т х п, т - число горизонталей; л - число вертикалей (рис. 3.8).

На квадратной доске размером kxk можно /И способами расставить владей. Различных досок kxk на доске тхп можно выбрать способами Рис. 3.8

С*С*. Отсюда rk =С*С„* Л!-число способов расставить владей на исходной прямоугольной доске. Тогда R(x, С) =

Задача. Найти R(x, С) для прямоугольной доски С размером 2x3.

Решение.

R(x,C) = %CkCkklxk =Сг0Сз00!х0+С,2СУьл1 + C27Ci22ix2-= 1 + 6х + бх2.

Коэффициент при х2 показывает, что число способов поставить две ладьи на такую доску равно 6.

ikf-<k

3.6.2. Многочлены попаданий

Определение. Пусть дана квадратная доска

размером л х л с запрещенными позициями

(рис. 3.9). Обозначим через Е„(к) количество

перестановок на квадратной доске л ладей, k

из которых занимают запрещенные позиции.

Многочленом попадания называется произ-

п

водящая функция E(t) =Еп(к)t последо- рис 39 вательности \Е„(к)}.

Установим связь между многочленом попаданий и ладейным многочленом. Введем обозначения:

Sn = {я, я2,..., п„\) - множество всех перестановок л ладей на доске л х п;

П = {©1, ©2,...} - множество весов;

со: Sn -И] - весовая функция, га (я) е - вес перестановки я е S ;

- запрещенных клеток на доске л х л;

РьРг,...,Рт - свойства перестановок; я е Sn обладает свойством Рр если ее ладья занимает запрещенную позицию j. Р( Л = J1, если я обладает свойством Pj,

\ О, в противном е. W(Pj = - сумма весов перестановок со свойством Pj,

W(pj,ph-p. ) = Р,Ы)Р^Ы)...Р^(кЫк) сумма весов

перестановок со свойствами Р} Pj2-Pjk \

lVk)= У^Щ\. Pj\--P ),)>> суммирование выполняется по всем

сочетаниям (jj2-.h) Длины k из т свойств, число сочетаний Принцип включения и исключения позволяет определить Еп(к)= Скк Щ)-С*+1 Wik +1)+..M-Dm-kСккЛм к)\¥(к + (т -к)).

Так как нас интересует лишь количество перестановок, то будем полагать ю(я) = 1. Нетрудно установить, что Щк)= гк(п - к)\, где гк - количество способов расставить владей на запрещенных позициях доски я х и. Тогда

Еп (к) = С\гк(п -к)\-СккЛгк+{п -к +1)1+.. .+(-1)т-кСкгт(п -т)\.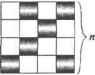

Заметим, что/* = 0 для всех к > п. С другой стороны, если т <п, то гк = О для всех к> т. Поэтому последнее выражение примет вид En(k)=CJkirk(n-k)\-Ck+lrk+l(ii -к+1)1+.. .+(-1) кСкгп (л -и)! или

п-к

Е„(к) = (-1) Ck+jrk+!(n-(i + Найденное выражение позво-/=0

ляет записать многочлен попаданий в виде

E(t) = ±Еп{к)*к = t Z(-D Cl,rk+I (n-(k+i))\tk.

fc=0 A=0i=0

Суммирование выполняется по координатам узлов сетки на рис. 3.10. Замена переменных суммирования А = к + i и в последнем выражении позволяет упростить многочлен попаданий и приво-

п к . .

дит его к виду E(t) = (-1) Ckrk(n-k)\t , где

к=ш=о

суммирование уже выполняется по узлам сетки на

рис. 3.11. Таким образом,

п ( к Л

£,(0 = ХГ£ Х/.-!) С'к-tk~ (п-к)\ или к=о \i=o )

E{t) = ±rk{t-\)k{n-k)\.

Jt=o

Для более компактной записи последнего выражения введем оператор Е~ , действие которого распространим на функции целочисленного аргумента: е 1(Д/г)) =Ап- 1) и г~к(/[п)) =Ди - к). Например, е~1(п\) = (л - 1)! и е~~*(л!) = (л - к)\.

Заметим, что [(/- \)z~x\kn ((- 1)*е~*я! = (t- 1)к(п - Ас)!.Тог-да многочлен попаданий перепишем в виде

т=Хгк(г-1)к( -кУ-=Тгк1(*--1>к^=

Рис. 3.11

А = 0

гАх* =R(x)nl ,

гдех = (г - 1)е . Таким образом, E(t)= R((t- l)z~x) п\.

Задача. Найти многочлен попаданий для доски 3 х 3 с запрещенными позициями на рис. 3.12. Запрещенные позиции отмечены темным цветом.

Решение. Найдем ладейный многочлен доски запрещенных позиций, которая состоит из двух неза- Рис. 3.12 висимых досок. Тогда

Щх) = Д® ДДВ) = (1 + Х)(1 + Зх + Х2) = 1 + 4х + 4.Г + х3.

Щ =R((t-\)z~l)n\=(\+A{t-\)z~l+4[(t-\)z~ l]2+[(t- 1)е 1]3)3! = = 1-3! + 4(t- 1)б 13! + 4[(f- 1)е-1]2 3! + [(t- l)s~lf 3! = = 3! +4(f- 1)2! i 4(f- l)2 1! + (t- 1)30! . Итак, E(t) = l + 3t+t2 + t3.

Анализ коэффициентов ДО при t показывает, что число перестановок, в которых ладьи не занимают запрещенных клеток, равно 1 (коэффициент при Г); перестановок с одной ладьей на запрещенных позициях - 3 (коэффициент при г1); перестановок с двумя ладьями на запрещенных позициях - 1 (коэффициент при t ); перестановок с тремя ладьями на запрещенных позициях -1 (коэффициент при t ).

3-2697

- Глава -

Генерация комбинаторных объектов

О комбинаторных алгоритмах часто необходимо порождать и исследовать все элементы некоторого класса комбинаторных объектов. Наиболее общие методы: решения таких задач основываются на поиске с возвращением, однако во многих случаях объекты настолько просты, что целесообразнее применять специализированные методы. Задачи, требующие генерации комбинаторных объектов; возникают при вычислении комбинаторных формул. Например, часто приходится вычислять суммы, имеющие вид

где суммирование выполняется по всем последовательностям удовлетворяющим некоторым ограничениям. В алгоритмах порождения комбинаторных объектов нас прежде всего будет интересовать сложность алгоритмов, т.е. общее количество времени, требующегося для порождения всего множества объектов.

4.1. Поиск с возвращением

Использование компьютера для ответа на такие вопросы, как сколько существует перечислите все возмож-

или есть ли обычно требует исчерпывающего

поиска множества решений. Метод поиска с возвращением постоянно пытается расширить частичное решение. Если расширение текущего частичного решения невозможно, то возвращаются к более короткому частичному решению и пытаются снова его продолжить.

Идею поиска с возвращением легче всего понять в связи с задачей прохода через лабиринт: цель - попасть из некоторого заданного квадрата Я в другой заданный квадрат Хпутем последо-

вательного перемещения по квадратам. Трудность состоит в том, что существующие преграды запрещают некоторые перемещения. Один из способов прохода через лабиринт - это двигаться из начального квадрата в соответствии с двумя правилами:

в каждом квадрате выбирать еще не исследованный путь;

если из исследуемого в данный момент квадрата не ведут неисследованные пути, то нужно вернуться на один квадрат назад по последнему пройденному пути, по которому пришли в данный квадрат.

Первое правило говорит о том, как расширить исследуемый путь, если это возможно, а второе правило - о том, как выходить из тупика. В этом и состоит сущность поиска с возвращением: продолжать расширение исследуемого решения до тех пор, пока это возможно, и когда решение нельзя расширить, возвращаться по нему и пытаться сделать другой выбор на самом близком шаге, где имеется такая возможность.

Общий алгоритм

В самом общем случае полагаем, что решение задачи состоит из вектора (аь а2, а3, .) конечной, но неопределенной длины, удовлетворяющего некоторым ограничениям. Каждое Д., где А, - конечное линейно упорядоченное множество. Таким образом, при исчерпывающем поиске должны рассматриваться элементымножества(яа а3 .., а,) е Л, хА2х...х.4(, для = О, 1, в качестве возможных решений. В качестве исходного частичного решения примем пустой вектор () и на основании имеющихся ограничений выясним, какие элементы изАу являются кандидатами в а у. Обозначим это подмножество кандидатов через SyczAy. В результате имеем частичное решение В общем случае для расширения частичного решения от до

ak y, ak) кандидаты на роль выбираются из сАк. Если частичное решение не представляет возможности для выбора элемента ак, то Sk 0: возвращаемся и выбираем новый элемент Если новый элемент выбрать нельзя, возвращаемся еще дальше и выбираем новый элемент ак 2 и т.д. Этот процесс удобно представлять в терминах прохождения дерева поиска в