При первом подходе представления множеств используют как смежное, так и связанное размещение его элементов в памяти (рис. 2.8). Данные методы размещения подробно рассмотрены в п. 2.1 представления последовательностей.

#

Рис. 2.8. Смежное и связанное представление множества в памяти Как и для последовательностей, наилучший метод представления множеств существенно зависит от операций, которые мы собираемся вьтолнять над ними. Типичные операции над множествами: выяснить, имеется ли конкретный элемент в данном множестве; добавить в множество новые элементы; удалить элементы из множества; вьшотшить обычные теоретико-множественные операции, такие как объединение или пересечение двух множеств. Как правило, для представления множеств применяют связанную память.

При втором методе множество представляется в виде вектора на смежной памяти. Пусть U - универсальное множество (т. е. все рассматриваемые множества являются его подмножествами), состоящее из п элементов. Любое подмножество S<Uпредставляется в виде характеристического вектора из п элементов. Элемент i в этом векторе равен 1 тогда и только тогда, когда /-й элемент множества Uпринадлежит S, в противном случае он устанавливается равным 0 (рис. 2.9).

Представление в виде характеристического вектора удобнее тем, что можно определять принадлежность /-го элемента множеству за время, не зависящее от его размера. Основные операции над множествами, такие как объединение и пересечение, можно осуществлять как операции v и л над двоичными векторами. Недостаток этого представления заключается в том, что операции объединение и пересечение занимают время, пропорциональное мощности универсального множества U, а не рассматриваемого множества S. Данное представление требует дополнительной памяти для хранения характеристического вектора, что для больших п (размер универсального множества U) бывает практически невыполнимо.

1 1 1 1 0 0 1 0 0 1 1 0 0 0 1 0 1 1 1 0 0

-1-1-1-1-1--1-1-!-1-1-J I 1 I 1 1 . i I 1 I

Рис. 2.9. Представление множества характеристическим вектором

=====-- Глава 3 --

Методы подсчета и оценивания

Рассмотренные в предыдущих разделах комбинаторные формулы подсчета означают вычисление или определение свойств некоторой последовательности чисел, соответствующие той или иной задаче. В этом разделе предлагается полезный инструмент для работы с последовательностями. Идея состоит в том, чтобы каждой числовой последовательности сопоставить функцию действительного или комплексного переменного, с тем, чтобы обычные операции над последовательностями соответствовали простым операциям над соответствующими функциями. Аналитические методы работы с функциями оказываются проще и эффективнее, чем непосредственные комбинаторные методы работы с последовательностями.

3.1. Производящие функции

Пустьtff. а2.... - произвольная последовательность. Сопоставим последовательности функцию действительного или комплексного переменного:

А(х) = акхк. (3.1.1)

Функция А(х) называется производящей функцией последовательности щ, аь а2,.... Какправило, поискфужщтА(х) по формуле (3.1.1) прямыми методами является сложной задачей. Однако заметим, что последовательность {ак} может быть восстановлена по А(х). Выражение (3.1.1) является разложением в ряд Тейлора в окрестности точки jc = 0. Воспользуемся этим замечанием и приведем некоторые наиболее распространенные производящие функции и соответствующие им последовательности.

Производящие функции А(х) Последовательности {ак}

Задача. Найти число Аг-мерных граней в -мерном кубе. Решение. Обозначим через ак число А>мерных граней в -мерном кубе, где 0 < к < п. Тогда производящую функцию последовал

тельности {ак} можно записать какД, (х)= акх. Индекс п для

А„(Х) показывает размерность куба. Например, А0(х) = 1, Ау(х)= 2+х, А2(х) = 4 + Ах + х2. Рассмотрим производящую функцию An+i(x)последовательности {ак}для (п +1)-мерного куба. Заметим, что (и +1)-мерный куб можно получить из мерного куба сдвигом последнего по (я +1)-му измерению. На рисунке показан пример получения трехмерного куба сдвигом по третьему измерению квадрата (двухмерного куба). Отсюда видно, что (я +1) мерный куб включает два старых -мерных куба и каждая А-мерная грань при сдвиге переходит в (к +1)-мерную грань. Из приведенныхрассуждений следует, что

Ап+1(х) = 2А„(х + х А„(х) где AQ(x] = 1.

Ап+1(х) = (.2+х)Ап(х) = (2 + хУ+1.

Воспользуемся разложением бинома Ньютона:

Ап(х)=(2+х)п =±Спкхк2п-к =±акхк.

4=0 к=0

Сравнивая коэффициенты при степенях/, получим, что число -мерных граней в -мерном кубе равно ак =2 кСк. Например,

А3(х)=23-°С%х° +23 1С]х1 +2ъ~2С}х2 +2ъ-ъС]хъ= 8 + Их + бх2* +Х3.

Простейшие производящие функции (3.1.2)-(3.1.9) будем использовать как строительные кирпичики для получения производящих функций более сложных последовательностей. С этой целью рассмотрим наиболее важные из операций над производящими функциями, т.е. способы получения новых производящих функций и соответствующих им последовательностей. Обозначим через последовательности, а соответствующие им производящие функции - какЛ(.х), В(х), С(х).

3.1.1. Линейные операции

Если ос и Р константы, то последовательность = a ак + p

имеет производящую функцию = ос А(х) + (3 AN л .

Например, последовательность соответствует производя-

г , s

щей функции - ,апоследовательность,\-1соответствуетпро-

1-х [klj

изводящей функции f, тогда последовательность \ 100+ - соответствует производящей функции -°+ 5е.

1-JC

3.1.2. Сдвиг начала вправо

Пусть последовательность определяется через последовательность следующим образом:

Ьк = 0 для к = 0, 1,..., / - 1 и

= дА. ,-для к = i, i + тогда В(х) =хА(х). Действительно

В(х) = ±Ькхк =±ak sxk * ±акхк =х'А(х).

к=0 k=i k=i Ш

3.1.3. Сдвиг начала влево

Пусть последовательность определяется через последовательность следующим образом: А = ak+h к = 0, 1,.... тогда

Г ы ,1 .

В(х)~ A(x)-y,akxk х~.

Действительно

*=0 к=0 к-0 k=i

т кхк-£ к*к ПАх^к*

А=0 *=0 А=0

3.1.4. Частичные суммы

Пусть последовательность определяется через последова-

тельность следующим образом:

bk =й, , к = 0, 1,.../тогда В{х)=--.

1=0 *~х

Действительно

В(х)=±Ькхк =t{i°i\l

А=0 *=0Y=0 }

1 2 3 4 к

Множество пар точек (к, /), по которым ведется суммирование, представлено на рисунке. Изменим порядок суммирования (сначала по i, затем по к). Выражение для В{х) примет вид

г к to ( *i \ ( ва V w \ 1

3.1.5. Дополнительные частичные суммы

Пусть последовательность определяется через последовательность {ак} следующим образом:

Ък = £°/. * = 0. 1,-, тогда В(х)=Л{1)- .

/=1с 1-Х

Действительно

Jfc.0V.i-Jt )

Множество пар точек (к,1), по которым ведется суммирование, представлено на рисунке. Изменим порядок суммирования (сначала по затем по К). Выражение для В(х) примет вид

О

1 2 3 4 к

( со / j \ 00 1 .,/+1

i=0 А=0 /=0 U=0 J /=0

1-х

2> j=

/ Д(1)-л.Л(х)

1-х

О (=0

3.1.6. Изменение масштаба

1. Пусть последовательность определяется через последовательность следующим образом:

Ьк = к ак, тогда В(х) - х А'(х).

Действительно

или

А(х) = акхк и Л'(х) = Ао4:с

it=0 А=0

х-А'{х) = Фак)хк =В(х).

2. Пусть последовательность определяется через последовательность следующим образом:

bt =--, тогда В(х) =-: [А(х)ах. к+Х х

Поскольку } = /: .* % то

Wkc = £ )акхках = £-хк+1 =х%Ькхк =х В(х)

П А=0 о А=0*+1 4=0

/=0 k=i \i=0

1-1 £A.r* \ = A(x)-B(x).

J U=o J

Далее обсудим наиболее общие приемы использования производящих функций на примере решения следующих задач.

Задача. Рассмотрим обобщенное биномиальное правило раскрытия выражений.

где обобщенный биномиальный коэффициент Тогда

(1-ху ыФ-К J * * *=о

Рассмотрим полученное выражение при = =(l-X)/2yx)k =

3.1.7. Свертка

Последовательность к

ck=lZaibk-i>k= 0, 1,...1тогда0д= А(х) -В{х).

00 00

Действительно, А(х) = акхк и В(х) = 2>Ах* > Т0ГДа

к^0 *=ОМ = 0 )

со -о f 00 \ ! 00

, f( l)2k-i\-\-3-5-7...Qk-3) к А \-3-5..Дк-Ъ) к

U 2кк\ к 2кк\

, Л-2-34-5-6-(2А;-3)(2А.-2) к к х -

fci 2 /с!-2-4-б...(2А:-2)

, f,l-2-3-4-5-6...(2*-3)(2*-2) к

- 1 7--л -

£1 2*)к!2*-ЧЛ-1)!

Таким образом,

4=1 4*£

Рассмотрим - при 1.

(1-х)

4=0Х-

где

V.& J к\ к\

Следовательно, - =(1-х) 1 = £(-1)* (-*)* = >*.

Задача. Сколькими способами можно разбить выпуклый (я + 3) -угольник (л > 0) на треугольники диагоналями, не пересекающимися внутри многоугольника?

Решение. Пусть ы„+3 - искомое число способов разбить (н + 3)-утольник на треугольники. Перенумеруем вершины исходного многоугольника числами от 1 до л + 3. Заметим, что при любом разбиении найдется треугольник, содержащий ребро многоугольника с вершинами и + 2ия + 3. Третья вершина этого треугольника может быть любой из остальных Пусть это будет вершина к. Если удалить треугольник с вершинами п + 2, п + 3, к, то получим два многоугольника с числом вершин к + 1 и

п + 3 - к, которые можно разбить на треугольники и и„+з-А способами. Суммируяпо£= 1, 2,..., п + 1, получим (согласноправилам прямого произведения и суммы) искомое число разбиений исходного (я + 3)-угольника на треугольники:

ил+3 = 2 ил+2+ w3 мл+1 + 4 мл-0 + - мл+1 и3 + мл+2 м2>

где п 0 и положили = 1.

Получили нелинейное рекуррентное соотношение для последовательности {ип+2}, п > О, для поиска которой удобно ввести новую последовательность п 0, такую, что v = wn+2, n>Q.

Тогда рекуррентное соотношение перепишется в виде

vn+l = Щ vn+o + vi vn-l + vn-2 + vi + vn-o vq> или

Заметим, что правая часть является сверткой двух одинаковых последовательностей {v } и {v } (см. п.3.1.7 операцийс производящими функциями). Ввиду этого, составим производящую функцию правой части

Пусть - производящая функция последовательности {v }, п 0, тогда последнее соотношение запишем как

Отсюда K(jc) = - (1±V1-4jc). 2х

Ранее рассмотренное разложение обобщенного бинома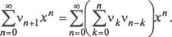

(У(\)- vt,) - /(х)У(х) или х V {x - V(x)+ 1 = 0.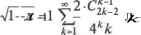

запишем для случая

4\-*х \-±\с£2*к.

Поскольку результат V(x) должен быть рядом по неотрицательным степенямх*, то решение К(х)=(1/2х)(1 + л/1-4х)является посторонним. Окончательно

Отсюда ия+,=ул=-г-, я 0.

Ответ: число способов разбить выпуклый (л + 2)-угольник на

треугольники непересекающимися диагоналями равно - -, л >0.

Задача. Найти сумму I2 +22+...+А:2 = £/2.

Определим четыре последовательности и их производящие функции:

ак = 1, Ък = как, ck=kbk, dk = £/2 жА(х), В(х), C(x),Z>(x).

/=о

Для решения задачи необходимо найти dk. С этой целью определим D(x), что позволит нам установить значения dk,

Дх) = °2Zdkx. Последовательности Ьк и ак связаны изменением

масштаба , значит Я(х) = х - А'(х) ПоследовательностискиЪктакже связаны изменением масштаба , следовательно,

С(х) =хВ{х) = х(хА(.х)У=хА\х)+х2А (х). Последовательности dk и ск связаны частичной суммой , тогда

С(х) х-А\х)+х2А (х)

L\x) = -=----

1-х 1-х

А(х)1-хк=-±-, А\х)~ (х)--. *~о 1 * О--*)2 (1-х)3

ОкончательноДх)=---i.

(1-х)4

Для получения коэффициентов воспользуемся разложением (3.1.9):

ОП * л л НО

л

-х)4 *=0V * / *=0