равным произведению весов

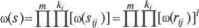1=1 >1 Ы У=1

имеем и(5)= Wfime/е А подчинена разбиению.

Для множества выполнены все условия правила обобщенного произведения, тогда сумма весов элементов данного множества, а значит, и сумма весов всех функций/ е А составит

т Р т

вследствие )

Ы\ Jgtg l=i

W(SV) = W ф) = £[ca(r)f =Д(ш'). Следовательно,

иж Х Ч/) =[Л( 1 2)]*2)]*

ПУСТЬ е G И g = (р, )(р2 ).. .(PAi Xpfi )(р, 2 )......(рд Р;2 ...Р7га )

разложение на независимые циклы, где (khk2,..., km) - характеристиками! - кх + 2 - k2 + ...+m - £ш = т.За1шшемразложениена независимые циклы в виде

g =(Al)(A2)---(A2l)(22)---(:--yMl)(2X-J X

где Dy - цикл длины /, Ду = i.

Обозначим разбиение множества В на By через Ag. Элементы d e Zty одного цикла при умножении на g переходят последовательно по циклу в элементы того же цикла. Указанное свойство позволяет заключить, что Vdbd2 е By Зк g*i= d2.

Пример. Пустьg= (12345)(678), тогдаg2 = (13524)(687). Определение. Функция/ е S называется неподвижной относительно g еС, если W e 7) /(g*/) =f(d).

- Утверждение 7.9.2. Функция/eS неподвижна относительно g е G тогда и только тогда, когда f е Ag подчинена разбиению

Доказательство. (=>) Пусть dud2eDy- принадлежат одному циклу. Следовательно, Sk g% = d2. Tovp.af{d2)=f{gkdl)= =f(g(?f~idl)=f(gk-ldl)= ... =f(gd1)=f(dly где каждый переход

7.10. Цикловая структура групп подстановок

Рассмотрим несколько общих примеров, которые в какой-то степени дают представление о возможностях изложенной выше техники подсчета классов эквивалентности с использованием теории перечисления Пойа.

обусловлен неподвижностью/: VdeD f(gd) =/(йО.Таким образом, Vdu d2 е D0 f(d{) =f(d2), т.е. /е Ag.

(<=) Пусть d eDy, тогда и gd tDi} - свойство циклов. Имеем /e Ag или d2 e Dyfidy) =f(d2 следовательно, \if(gd) = f(d), тогда /есть неподвижная относительно e G.

Запишем сумму весов/ подчиненных разбиению Ag, в следующем виде W(/= в^ш-со, где-количество функций,

feAg fflsQ

подчиненного разбиению Ag, с весом ю eQ.

Составим множество всех функций, неподвижных относите-льно# e G, с весом ш eQ : xViSI(g) = sJ\ydeDf(gd}=f(d/\PV(J = со}. Утверждение 7.9.2 позволяет записать - Ч И(£). Величина Сга - число классов эквивалентности с весом со eQ, на которые распадается множество функций S = 5\иS2kj...-иSN под дейст-

вием группы G. По лемме Бернсайда, Сю = - У\ц,т(я)\ = = ГЯГ lT аД?,ш Умножив последнее равенство на со ипросуммиро-вав по всем весам из получим, что =

Сумма Xfl4s. .w= Е^-Я - сумма весов функций, подчиненных разбиению Ag.

Так как Ж(/) =[Дсо1 [Л(оз2)...[Дшт)]*- , то

7.10.1. Цикловой индекс группы, действующей

на себе

Пусть группа Gдействует на множестве G следующим образом : Vg е G Vse Sg{s) = gs. Если порядок элемента g = 4, то все элементыgs,£s, gs,...,/j= различны. Группа (распадаетсяпод действием g на циклы одинаковой длины. Количество циклов равно d, где = \ G - порядок группы. Цикловой индекс группы примет вид

Z(G\x, ,л>......< )~ Y.-AdyxHjd, (7.10.1)

\G\ d/n

где у( d) - количество элементов g е G с порядком g = d. Суммирование выполняется по всем делителям d числа п.

7.10.2. Цикловой индекс циклической группы

Пусть S= {0, 1,.. /7-1} - множество вершин правильного -угольника (рис. 7.6) на плоскости. Группа G - циклическая группа самосовмещений. Образующий элемент группы а е G - вращение (отображение) S вокруг центра на угол 2п/п. Следовательно, G= {а = е, а, а а ~1}, где е - тождественная подстановка. Если обозначить вершины многоугольника {0, 1,..., п-1} элементами группы {а =е, а, а1,..., ап~1}, то вращение будет эквивалентно умножению вершины на соответствующий элемент группы. Например, совмещение при вращений на угол 2п/п равносильно умножению новых меток {а = е, а, а2,..., а 1} вершин л-угольника на элемент а, действите-

2 л-1

льно, а е-*а, а а->й а й - а . Таким образом, можно считать, что циклическая группа G действует на себе. Согласно (7.10.1) цикловой индекс данной группы примет вид

d/n d/n

где y(d) - ф (d) - функция Эйлера. Действительно, если порядок элемента равен d (элемент суммируется ву(йО), то он является образующим элементом подгруппы Я с G порядка \Н\ = d. Показать, что если порядки элементов циклической группы совпадают

Рис. 7.6

Z(G,xvx2,...,xn)~y{d)x*Jd =±d)x d

(7.10.2)

8-2697

\ак\ = \ат \ = d, то они являются образующими одной и той же подгруппы Яс G. Число образующих в такой подгруппе ср(</).

Найдем количество возможных раскрасок двумя цветами вершин данного (рис. 7.6) -угольника. Пусть цвета - .К = { ,<>}. Воспользуемся теоремой 7.9.1 Пойа. Для определения количества раскрасок положим веса цветов равными ©( ) =1 и со(°) =1. Тогда Д(<й*) = < *(.) + ю*(о)=2.

Для треугольника = 3) число раскрасок равно

Nc =2 /d =г\(2 +Ф(3)21) =k-23+2-21) = 4.

Для шестиугольника число раскрасок равно

NG =-Yd)2n/d= Гф(1)23 +ф(2)23 +ф(3)22 +ф)21\ =

о(1.2Ч1.2з+2.2Ч2.214.

7.10.3. Цикловой индекс симметрической

Пусть S= {1, 2,..., л} - произвольное множество, на котором действует группа всех подстановок - симметрическая группа, \Sn = п\. Рассмотрим произвольную подстановку п s Sh с характеристикой (ки къ..., кп), где \кх + 2к2 + ... + пкп = п. Подсчитаем количество подстановок с данной характеристикой. Для этого запишем в цикловом представлении, помещая знаки - на местах, которые должны занять п элементов. Так, для характеристики (3,2) следует записать (-)(-)(-)( - )(--). Далее пробелы можно заполнять п элементами множества S в любом порядке. Это дает и! подстановок с характеристикой (kki,..., к„), которые, однако, не все различные. Каждый из циклов может начинаться с любого своего элемента, не изменяя исходной подстановки и уменьшая общее число различных подстановок в г раз. Если имеется кг таких циклов, то их можно переставлять способами, что также не будет приводить к новым подстановкам. Все эти варианты суть

различные обозначения одной и той же подстановки с характеристикой (кь к2,..., кп). Поэтому различных подстановок с указан-

©гда цикло-

ной характеристикой будет -

fcjbl 1 k2\-2kl ...кп\-пк вой индекс симметрической группы можно записать в следующем виде: Z(G, хьх2,..., х„) =

{ikli+2k1+...+nk.-nkA-l 1 кг\-2кг ...кп\-п'

xl x2 xf

Рассмотрим пример определения числа Nc раскрасок двумя цветами^ = { , °} трех усов 5 = {1,2, 3} антенны (рис. 7.7). Усы свободно вращаются в пространстве. В этом случае на множестве S- {1, 2. 3} действует симметрическая группа подстановок S3. Найдем все характеристики (%, к2, к3) разложения числа 3 = Щ + 2к2+Зк3. Ими будут: (3,0,0), (1,1,0) и (0,0,1). Цикловой индекс примет вид

2, 3 . Z(G, Ху Х2, Х3) =

Рис. 7.7

.KiV.i/iYraVJfaq1.

У\ 1 J 1Щ 1 Д 2 ) IM J

Для определения количества раскрасок положим веса цветов равными <а( ) 1 п ф) =1, тогда Д©*) = ев* ( ) + ш* (°) =2. Следовательно,

- Глава 8 ----Элементы теории чисел

I чисел занимается изучением свойств целых чисел.

Целыми называются числа Z= {..., -3, -2, -1, О, 1, 2, 3,...}.

Для любых a,b е Z сумма а + Ь, разность а - и произведение

п

а Ъ являются целыми числами. Но частное - от деления а на Ъ

Ь

(если b не равно нулю) может быть как целым, так и не целым. В

случае, когда частное - является целым, то обозначают а = bq, где Ъ

q - целое число, а тогда называют делителем числа а и записывают так: Ь\а. В общем случае единственньш является представление a = bq + r,0< г < b где - называют остатком от деления.

8.1. Наибольший общий делитель

В дальнейшем будем рассматривать лишь положительные делители чисел. Всякое целое, делящее одновременно целые с, называется их общим делителем. Наибольший из общих делителей называется наибольшим общим делителем (НОД)п обозначается (а, Ь, .., с). Если (а,Ь,.. с) = 1, то а, Ь,..., с называются взаимно простыми. Например, (10, 15) = 5, (8, 21) = 1.

Свойства наибольшего общего делителя

1. Если а = А* то (а, Ь)=Ь.

2. Если a = bq + r, тогда общие делители чисел ажЪ суть те же, что и общие делители чисел и в частности, (а, =

3. Для определения наибольшего общего делителя применяется алгоритм Евклида. Он состоит в нижеследующем. Пусть а и - положительные целые числа и а > Ь. Составим ряд равенств:

& = bqj + г2, 0 < r2 < Ь,

b=r2q2+r3, 0<r3<r2,

одз+ ГЬ 0 < Г4 < гъ (8.1.1)

= Ом<Уя-1 + < <

Vi = ггАю

заканчивающийся, когда получается некоторое г„+1 =0. Последнее неизбежно случится, таккакряд Ъ, г2, гь... убьгвающих целых чисел не может содержать более чем Ъ положительных.

4. Из формул (8.1.1) алгоритма Евклида следует, что (а, Ь) = (Ь, Л) = (г2, г,) =... = (/ г„) = г„.

Наибольший общий делитель равен последнему не равному нулю остатку алгоритма Евклида.

5. Из формул (8.1.1) алгоритма Евклида следует также, что существуют целые tv и t2, что tya + t2b = гп. В частности, если (а, Ь) = 1, то txa + t2b = 1.

Пример. Найдем (525, 231). 525 = 231 -2 + 63, 231 = 63-3 +42, 63 = 42-1 + 21, 42 = 21 2.

Последний остаток есть 21, значит, НОД = (525, 231) = 21.

6. Пусть т - любое положительное целое, тогда (am, bm) = = (а, Ъ)т.

7. Если (а, Ъ) = 1, то (ас, Ь) = (с, Ь).

8. Если (a, b)= I и ас делится на Ь, то с делится на Ь.

8.2. Наименьшее общее кратное

Всякое целое, кратное всех данных чисел, называется их общим кратным. Наименьшее положительное общее кратное называется наименьшим общим кратным (НОК). Наименьшее общее кратное двух чисел а и b равно их произведению, деленному на их общий наибольший делитель, т.е. .

8.3. Простые числа

1. Число 1 имеет только один положительный делитель, именно 1. В этом отношении число 1 в ряде натуральных чисел стоит совершенно особо.

Всякое целое, большее имеет не менее двух делителей, именно 1 и самого себя; если других делителей нет, то число называется простым. Целое, большее 1, имеющее кроме 1 и самого себя другие положительные делители, называют составным.

2. Наименьший отличный от единицы делитель целого, большего единицы, есть число простое. В противном случае, можно

было бы выбрать делитель еще меньше.

3. Наименьший отличный от единицы делитель (он будет простым) составного числа а не превосходит 4а. Действительно, пусть q - именно этот делитель, тогда a = qbab>q(q- наименьший делитель), откуда а > q или q <4а.

4. Простых чисел бесконечно много. Это следует из того, что каковы бы ни были различные простые числари р2,..., Рь можно получить новое простое, среди них не находящееся. Таковым будет простой делитель суммы Рхрг...рк + 1, который, деля всю сумму, не может совпадать ни с одним из простыхрьр2,-,Pt

5. Решето Эратосфенадля составления таблицы простьк чисел. Данный способ состоит в следующем.

Выписываем числа

1,2, 3,4, 5, 6,7, 8, 9, 40, 11, ...,7V.

Перное, большее 1, число этого ряда есть 2. Оно делится только на себя и на 1 и, следовательно, оно простое. Вычеркиваем из ряда (как составные) все числа, кратные 2, кроме самого себя. Первое, следующее за 2 не вычеркнутое число есть 3 - оно также будет простым. С ним, как и с числом 2, проделываем ту же процедуру и т.д. Если указанным способом уже вычеркнуты все числа кратные простьк, меньшихр (4а <р),то все невычеркнутые, меньшие р2, будут простые.

Составление таблицы простых чисел, не превосходящих N, закончено, как только вычеркнуты все составные кратные простых, не превосходящих 4N.

В алгоритме 8.1 реализовано решето Эратосфенадля нечетных чисел 2N+ 1 с предпросеиванием для двойки; другими словами, начинаем только с нечетных чисел, отсеивая кратные 3, 5, 7, 11 и т.д. Вектор .Уявляетсядвоичным набором индикаторов простьк нечетных чисел. Так элемент вектора Xk- 1, если соответствующее ему число 2к + 1 - простое; в противном случае, когдаХк = О, число + 1- непростое.

Алгоритм 8.1. Решето Эратосфена

Х=(\, 1,-, 1): for к= 3 to V2JV+ 1 by 2 do

{Xk-l)/2~ индикатор нечетного числа k) {Вычеркнуть числа кратные к)

tfX(k-\)/2 = 1 thenfar i = k2to2N+iby 2к do Ун)-\)/1 = 0; { Печать простых чисел } fork=\ to Ndo ifX 1 then вывести 2k + 1.

Рабочая программа на языке Pascal реализации решета Эратосфена генерации простых чисел приводится в алгоритме 8.2. Алгоритм 8.3 - это пример реализации алгоритма решета Эратосфена на языке Си.

Алгоритм 8.2. Программа на Pascal е генерации простых чисел

Program PgmPrimary; {Программе генерации простых чисел)

uses CRT;

Const

N=4 5; {Простые числа среди 3,5,...r2*N+l} Туре

Vector=array[1.. N] of Boolean; Var

f :Text; {Текстовый файл простых чисел)

X :Vector; {Вектор индикаторов простых чисел)

Procedure Primary; {Генерация простых чисел) Var

i,k,M,nm :Integer;

begin

nm:=2*N+1;

for k:=l to N do X[k]:=TRUE; k:=3;

M:=trunc(sqrt(nm)); while k<=M do begin

if X[(k-l) div 2] then begin

числа кратные while i<=nm do begin X[(i-1) div 2]:=FALSE; i:=i+2*k; end; end;

нечетные числа

end;

(Печать простых чисел по индикаторам Xfk]} is 5=0;

for k:=l to N do if X[k] then begin i:=i+lf

Write (f,2*k+l, ) ;

end; WriteLn(f) ;

простых нечетных чисел + диапазоне[3 2*N+1, ] равно , f) ;

end; begin

Assign (f, Primary, out ) ; {Файл для записи простых чисел } Rewrite (f) ; Primary; Close (f); end.

/Luopunut 8.З. Программа на Си генерации простых чисел

#include <stdio.h> #include <math.h> ttdefine N 45

char X[N+1]; Индикаторы простых чисел

в диапазоне 3,5,. . . ,2*N+1}

int main (void) (

FILE *f;

int i, k,M, run;

f =f open ( primary, out , wt ) ; Файл для записи

простых чисел

nm=2*N+l; M=sqrt (rim);

for( k=l; k<=N; k++ ) X[k]=l; for( k=3; k<=M; k+=2 )

if ( X[(k-l)/2] )

for( i=k*k; i<=nm; i+=2*k ) X[ (i-l)/2]=0;

простых нечетных чисел

i=0;

for( k=l; k<=N; k++ )

if(X[k]){ i++; fprintf (f, %d ,2*k+l); }

простых нечетных чисел в диапазоне [3,%d] равно %d ,2*N+1, i) ;

f close (f) ;

return 0;