Свойство 1. Для верно, что \/ах * я2 р. Ат ф(я,) *ф(я2), в противном случае яjt = я2т. Отсюда, умножая справа последнее равенство на т, получим ятт) а2{$\), а так как тт = е, тощ = я2, что противоречит выбору Я] Ф а2.

Свойство 2. Для любой нечетной подстановки Ъ существует прообраз Ьх еАт четной подстановки, так как щ{Ъх) = (Ьх)х = Ыхт) = Ь

Свойства 1, 2 позволяют утверждать, что отображение ф является взаимно однозначным.

Утверждение7.6.2.Ат - подгруппа симметрической группы

Теорема7.6,5Кэли, Всякая конечная группаGпорядка т изоморфна некоторой подгруппе симметрической группы Sm.

Доказательство. Для любого элемента а е G рассмотрим отображение Lu : G G, состоящее в умножении всех элементов G= {gi,g2,..., gj слева на a: La(g,)= вд. Свойство группы aG= G позволяет утверждать, что La - взаимно однозначное отображение (подстановка). Обратным к La будет отображение L} =Z,

единичным отображением является Le. Вследствие ассоциативности умножения в группе G имеем замкнутость: (LaLb){g)= = = = = т.е. = Отсюда следует,

что множество H = {LgLgi,...,LgJ образует подгруппу в множестве всех взаимно однозначных отображений С в себя, т.е. в симметрической группе Sm. Тогда отображение ф: G-> Ястакое, что Vfl е (7ф(о = Lu есть изоморфизм, поскольку ф - взаимно однозначное и выполняется свойство <р(я£) = Lab = LaLb = ф(я)ф(о) сохранения операций.

7.7. Действие на множестве

Определение. Говорят, что задано действие группы Сна множестве S= {1,2,..., т}, если определен гомоморфизм Г группы G в симметрическую группу подстановок: G Свойство сохранения операций для гомоморфизма: Vft, g2 е G Tigr Si) = TXgi) ад. где

T(<t v ( 1 2 ... m) v

Далее полагаем, что g: = m \

Замечание. Чаще всего бывает так, что действие : на S возни -кает естественным образом, как группа симметрии структуры, определенной на S.

Пример. Пусть S = {1, 2, 3, 4, 5} - вершины графа на рис. 7.1. Найти G - группу самосовмещений данного графа.

Решение. Исходное множество элементов .Уявляет-ся связанным или структурой. Группа G, действующая на S, - группа самосовмещений: G = {е, a, b, ab},

где е

9 4

тождественное преобразование;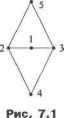

поворот

а =/1 2 = (45)

вокруг горизонтальной оси;

Таблица 7.1

3 2 4

(23)-

поворот

поворот

вокруг вертикальной оси;

ab=\\ 3 2 ffi (23X45)

вокруг горизонтальной оси и вертикальной. В табл. 7.1 содержатся все возможные произведения элементов рассматриваемой группы. Из табл. видно, что G - коммутативная группа и G={e, а}х{е, Ъ).

Определение. Элементы* s2 e Sназываютсяц-жбивтснтны-

ми и записывают sx ~ s2, если 3g е G, который, действуя на

г

множестве S, переводит Si в .$2, т.е. g =

... т о..

или

ОС j ОС 2*** *2*** J

более короткая запись этого .gSj = s2.

Утверждение7.7.1. Ощимтетищ-эквиваяентность на множестве S является отношением эквивалентности. Доказательство. Проверим свойства отношения эквивалентности.

1. Щ е S sx ~s2.

Действительно, щ =su где е &G- единичный элемент.

~2, WSl, S2 G О Sy ~ S2

Имеем Sj ~ s2, тогда 3gs G gs{ = s2ns2=g lsb а значит, s2 ~ sx

5. Vii, $- St, £ 6 5 j S-i A S-> ~ S3 -> S 53.

Имеем, что 3f, g e G ts} = л^ч = ,уз> откуда (tg)s =g(ts3J = ~-gs2 S3. Следовательно, щ ~%.

Утверждение?. 7.2. ГругшаС = {gu g2,...,gk} , действуя на множестве S, порождает его разбиение на непересекающиеся подмножества - классы эквивалентности (рис. 7.2): Л .У, .У-, . >..>S.-, , где Vjj у2 е 5а 3g e (У

- количество классов эквивалентности. Пусть s, <=S , тогда класс эквивалентности

Рис. 7.2 w У 1 а. м

.Уа составят все различные элементы множества Уа =

{ад.ад[.--,ад}-Определение. Множество Zu,) = e G \gsl=sl, s{ e называется стабилизатором Sj e .у. Элементы стабилизатора оставляют на месте.

Пример. Продолжим рассмотрение примера на рис. 7.1. 5= {1, 2, 3, 4, 5} - вершины графа на рис. 7.3. На £ действует группа самосовмещений G = {<?, а, Ь, ab}, где e=fl2 3 4 5) J\ 1 3 4 5\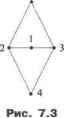

2 3 4 5/ -/2 3 5 4/ 2 3 4 51 лЬ Г1 2 3 4 5

3 2 4 5 3 2 5 4 Найдем все классы эквивалентности. 5 ,= Ml). а(1), b{\), ab{\)}= {1, 1, 1, 1} = {1},

S2= {e(2), a(2), b(2), ab(2)} = {2, 2, 3, 3} = {2, 3}, SV M4), я(4), a(4), д/>(4)) = 5, 4, 5/ = {4, 5}. S = 5, u.sius3- всего три класса эквивалентности. Определим стабилизаторы для вершин графа{1, 2, 3, 4, 5} . Z(l) = {е, а, Ъ, ab}, Z(2) = ДЗ) = {е, а}, Д4) = Д5) = {е, Ь).

Утверждение 7. 7.3. Z(si) с G - подгруппа группы G. Доказательство. Проверим свойства группы.

1. Замкнутость. g2 е Z(s{) gxsv = su g2s{ = sh тогда и fagA = =g2(Sisi) =feAi = следовательно, g\g2 e Z(s{).

2. Единичный элемент e e Z(sx), так как esx = sx.

3. Обратный элемент. Пусть g e Z(s{), тогда fSj = su откуда

j, следовательно, g~x e Z(jj).

Утверждение 7.7.4. vsx, s2 eSa \Z{sx)\ = \Z(s2)\n 3t eG Z{sx) =

= tZ(s2)fl- в этом случае говорят, что подгруппы Z{sx), Z(s2) сопряжены.

Доказательство. Имеем sx, s2 е Sa, следовательно, 3teG tsx = s2. Vge Zisi) {tg)s\ = g(tsx) gsj= s2 = tsxwm (tg)sx = tsx. Отсюда (tgt~l)sx = t~l(tg)sx= rl(tsx)= (tt~ )sx=sx, т.е. tgt~ e ад. Получили, что Vg e Z(s2) tgt e Z(sx). Заметим, что Vg, *g2 e Z(s2) tgxt~l ф tg2t~l, значит, \Z(s2)\ = \tZ{s2)rl\ \Z{sx)\vum Z(.s2)< \Z{sx)\. Подобным образом доказывается в обратную сторону: Z(s2)> \Z{sx)\, следовательно, IZlfo)! \Z(s2)\.Показали, что 3t &G Vge Z(s2) tgt1 e Z{sx) и >2T(i) = Z(s2) = \tZ(s2)t~l\,отсюда Z(sx) = tZ(s2)rl.

Утверждение 7.7.5. \Sa\= 11 , где*, eSa.

\Z(sx)\

Доказательство. Пусть G = .{gx,g2,..., gk). Из утверждения 7.7.2 следует, что Sa = {gxsx,g2su..., gksx), однако среди выписанных элементов множества могут встречаться одинаковые. Назовем

gi e G эквивалентными ~g(1, если они действуют на элементу одинаковым образом, т.е. g, sx =gjSx . Данное отношение является отношением эквивалентности. Введенная эквивалентность разбивает группу G на классы, количество которых равно числу различных элементов среди выписанных

т.е. равно

Пусть gjisx=giisx (g-gjj или fe1A21)*i=?r21fe1Ai) = SiliSii) = fe22)5i = i> следовательно, gixgll eZ(sx) или gh eZ(sx)giv Верно и обратное, если gh eZ(sx)gii, то gt\gll eZ(sx) или (ghgj])sx = sx. Отсюда g(]sx =ghslmm g -g,2.

Таким образом, ~ тогда и только тогда, когда , лежат в одном правом классе смежности по стабилизатору Z(sx) e а значит, и число элементов в равно количест-

ву правьк смежных классов в Gno подгруппе Z(sx). Согласно теореме 7.3.1 Лагранжа, \ Sa\= -М-Цб:, ).

Лемма 7.7.1 Бернсайда. Число классов эквивалентности, на которые распадается множество S = St (jS2u...uSnпод действием группы G, равно Mr, = Дг У u/(£)l, гае \\i(g) = {.ye-Sl даз}.

Доказательство. Подсчитаем двумя различными способами множество всех таких пар элементов, что Vg е G Vse S {(g,s)\gs=s). Это можно выполнить следующим образом:

leJ gzG

Первая сумма £Z(j)I = yjZ(s). Так как svs2eSa то yjZO) =5 -Z(sa) = M Z(5a) =С7где sa eSa. Таким образом, YJZ(j) = ZJZ)I= 1с1=лгс-1с1-

<=1*е5 =1

Получили, что откуда

Пример. Продолжим рассмотрение примера на рис. 7.3. 5= {1, 2, 3, 4, 5} - вершины графа. На J действует группа самосовмещений G={e, а, Ъ, ab}, где е =JjJ). и= 035 1).

L fl 2 3 4 54! л (] 2 3 4 51 1 I 1 3 Г: 4 5} UJ ~\\ 3 2 5 4/

Полным перебором установили, что под действием G множество распадается на три класса эквивалентности: S -.:>, u52 uS3,

где Sl ={1}, S2 ={2,3}, S3 ={4,5}. Установим данный факт, применяя лемму 7.7., Бернсайда: М G У \\i(g)\ - число классов экви-

\u\g*G

валентности.

Ч/(е)=фе = {1, 2, 3, 4, 5},

Hfd)= {se.Sas=j} ={1,2, 3}, y(b) = {se S\bs=s} = {\, 4, 5}, \y{ab) = {s€: S\ {ab)s = s} = {I}.

Отсюда следует, что число классов эквивалентности

NG =~(\ц1(е)\+\ у\)(а)\+\ \ф)\+\ \V{ab)\) = 1(5 + 3 + 3 +1) =3.

Замечание. Рассмотрению более содержательных задач, при решении которых возможно применение изложенной выше техники подсчета классов эквивалентности, предварим изложение теории перечисления Пойа. Это позволит нам с более формальных позиций подойти к пониманию самой техники подсчета и к применению ее для решения задач.

7.8. Цикловой индекс группы

Пусть группа С действует на множестве s= {1, 2,..., т} и т: G~> sm - гомоморфизм в симметрическую группу sm. Рассмотрим разложение g e G на независимые циклы

I, Aj Щ

где /ц - количество циклов длины 1: к2 - количество циклов длины 2;

А , - количество циклов длины т.

Набор (ки к2,..., кт) называется характеристикой элемента geG, где lfcj + 2 %+...+ т кт - т.

Определение. Цикловым индексом Z(G,xb х2,..., хт) группы G, действующей на множестве S, называется полином от переменных jc х2,..., хт, определяемый формулой

Z{G,xx ,х2 ,...,х/п) = - лс, 1х22 хт 1

где - характеристика элемента g

Пример. Продолжим рассмотрение примера на рис. 7.3. S= {1, 2, 3, 4, 5} - вершины графа. На £действует группа самосовмещений G= {е, а, Ъ, ab}, где е 2 3 4 fj а =(1 2 3 5 \\

b = (l 3 23 4 I) йЬ - f -айдем Цикловой индекс группы

G, для этого выполним разложение на независимые циклы подстановок элементов G и установим их характеристики:

е = (1)(2)(3)(4)(5), (кхк2...кт)= (5, О, О, О, О); а = (1)(2)(3)(45), (kik2,..km)= (3, 1, О, О, О); Ъ = (1)(23)(4)(5), (kik2...km)= (3,1, О, О, О); ab= (1)(23)(45), (кхк2...кт) = (1, 2, О, О, О).

+ х\х1х]х\хЬ =±(х? +ф| +х1х1г *®Ф% + х]х22).

7.9. Теория перечисления Пойа

Введем следующие обозначения. D - {db d2,..., dm) - конечное множество. G= {gi,g2, ftj--} - конечная группа, действующая на D. R = {\,г2, / з,...} - конечное множество качественных признаков (цвета).

S= {f\f-D-*R} - множество функций; каждая функция/определяет качественные признаки элементов D. Л = {ю\.ю2, ю3,...} - множество весов. : Ril - весовая функция, назначает веса и (г) е Q признакам reR.

Доз) = У^к>(>) - сумма весов элементов или

Him) - VC,/.:) , где - число элементов re R с весом е Q,

множество {С,} - перечень относительно весовой функции ш(г).

Рассмотрим введенные понятия на следующем примере, к которому ниже не раз будем возвращаться. Пусть D= {di, d2, d}} - вершины правильного треугольника (рис. 7.4). Треугольник нанизан на вертикальную ось, вокруг которой он свободно вращается. = - множество из двух красок. Найти количество

различных раскрасок вершин треугольни-Рис. 7.4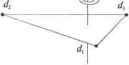

7.9. Теория перечисления Пойа.

На D действует группа самосовмещешгй G= /с, а, а2}, где е={\ 2 3) ~~ тождественное совмещение, а j fj~поворотво-

круг оси на 120°, а2 ={ \ ? \ j - поворот на 240°.

Q = {х, у, х~1, у~1 и их произведения}- множество весов. S = VI/D-+R} - множество раскрасок. В треугольнике три вершины и каждую допускается окрашивать в любой из двух цветов R = { > °}> следовательно, всего функций 23. Такое количество раскрасок будет, если треугольник сделать неподвижным (рис. 7.4). Если допустить вращение, то различные раскраски неподвижного треугольника становятся одинаковыми для вращающегося треугольника. Приведем пример трех раскрасок: f\,f2,fy /i : D -> Л, /3:Л-+Л,

ЛЦ) = , fiidy)-, /]Ц) = =,

/i(rf2) = *, /2(2) = °. & = i

/,№) = , /3<tf3> = °. /з(з) = °-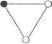

* 4 4

Очевидно, что для решаемой задачи раскраска/2 и/3 совпадают.

Назначим краскам Я = {♦, с} веса: -х и ш(°) =у.

Замечание. Отметим, что назначенные веса элементов =х и ю (о) =у позволяют сравнивать признаки количественно, забывая, в какой- то степени, о качественном их содержании.

- Определение. Для каждой функции/еЖ определим вес

W(f)=\\<b(f{d)).

В нашем примере = ш( М )и>(о) =хху = х у,

W(/3 ) =ш(о)ю(.){о(о) =ху =хк2-

Определение. Группа G- действуя на Д индуцирует (наводит, создает, определяет) свое действие на множество функций S. Положим V/ еS Vg e.G gf=f(g{d)) это рассматривается

В нашем примере рассмотрим действие элемента а е G на fz zS.

f2(a2(dx))=f2(d3) = ° и./) = ,

АИШ^вШ** И /3(> = °-

Таким образом, элемент группы а переводит^ в/3 или, в принятых обозначениях, a2f2=f.

Определение. Положим ft ~/2, если 3g е G VdeD fx(gd) = f2(d), Такие fx и /2 определяют одинаковые раскраски элементов rfe D.

Введенная эквивалентность функций есть от-

Аношение эквивалентности, которое порождает разбиение множества элементов/е S на непересекающиеся классы эквивалентности (рис. 7.5): * ... SKe S = SlvjSl...SNo,TyflJ2eSfl3g5Ggfx=f1 Рис. 7.5 И eSa eSV VgeGgfx*f2,S0*Sp, NG--количество классов эквивалентности. Каждый класс эквивалентности определяет отдельную раскраску элементов e D. Таким образом, количество различных раскрасок равно NG. Для определения NG воспользуемся леммой

7.7.1 Бернсайда: NG = г\- TJ\.\i(g) в данном случае

y(g) = {fe S\gf=fwmf(gc=Ad)Vd е D).

Вернемся к нашему примеру на рис. 7.4 и найдем для него число NG. ц>(е) = {fe S\ е/=/удовлетворяют все/е S, откуда \ц/(е)\ = = 23 = 8. ч>(а) = {fe S\af=f)- это такие раскраски/вершин, которые допускают совмещение с эквивалентной из раскрасок вращением треугольника на 120°. Это возможно, если все вершины либо белые, либо черные. Итак, у(я) = 2. Подобным образом устанавливается, что и v(a2) = 2. Следовательно, NG =i(S + 2 + 2)=4.

Утверждение 7.9.1. Если fx ~/2, то W{fx)=W(fl) ,т.е. эквивалентные функции имеют одинаковые веса. Доказателъство. D = {dx,d2, d3,...} и D - {gdxgd2, gd3,...} - верно e G, так как G действует на D и g j - это

L?tfi #<ъ s i i

7.9. Теория перечисления Пойа

подстановка. Теперь W(fl¥Yla<fi(d)) = IKfi(Sd))- Имеем

deD deD

fx ~ f2. тогда G Vd e DnWgd)) -- v>{f2{dj). Отсюда

Определение. Последнее утверждение позволяет определить вес каждого класса эквивалентности в разложении S - S{u

vjS2kj. . .u%, как W\S) = W(f)me / e I . Определение корректно, так как каждый класс .У, состоит из эквивалентных функций f веса которых совпадают.

Теорема 7.9.1 Пойа. £СШ ra = Z(G,.K(ra1),ra2),...,ram)), где

число классов эквивалентности S = Sx и S2kj. . .uSN( с весом га e Q, Z{G,xl ,Х22,...,хтт ) - цикловой индекс группы G, действующей на множестве D={db db..., dm}. Отметим, что

Доказательство. Пусть А - разбиение множества D на непересекающиеся подмножества:

D=Dn+Dn+...+Dlk +D2l +D22+...+D2ki+...+Dml+Dm2+...+Dmkm, ,-,-1- >.-v- -------

*, кг km

где = \d = m, 1 + 2- +... + т =

Определение. Говорят,что/е подчинена разбиению Д множества Dи записывают/е Д. если/постоянна на каждом подмножестве Dy из разбиения: е Dy Ad) = гу, где ry е R. Функция/, подчиненная разбиению Д , взаимно однозначно определяется набором (rnr12.. .rlkr21r22. .г2кг.. .rmlrm2. .гткт), где

Все такие наборы составляют множество:

S = SnxSi2x...xSlki xS2lxS22x...xS2k2X...xSml xSm2x..xSmkiii ,

> - v-1 --v- -Si-

где Sy - R, i = l,m,j = l,kj. Полагая веса элементов Sy e равными (a(sy) = [ю(гу)]пвесs= (S[lsl2...slks2ls22...s2k2...smlsm2...smkJ 6 S