Рис. 6.52. Начальная матрица ценностей

Шаг 1. Фиксируем все vrj-= \,п и уменьшаем значения i \,пдо тех пор, пока одно из неравенств и, + Vj > йц не обратится в равенство и, + V,- = щ Эту процедуру выполняем для каждой строки /= 1,и. В рассматриваемом примере на рис. 6.53 звездочками отмечены совпадения.

Рис. 6.53. Матрица совпадений

Шаг 2. Для каждого ,-,/ = 1. определим множества совпадений

$=У\ ,+ V,= Од), (= 1,П.

Если обратиться к примеру, то Sy = {2}, S2= {2}, S3 = {1}, SA={1).

Система множеств .5* / = l,n может иметь систему различных

представителей: е Sy,j2e S2,...,jne Sn, гдеj\, i2,...,jn - все раз-

£ i *э у\ \

личные. Тогда на перестановке я = .* выполняется со-

\J\ 72 Jn)

отношение и, +v;- -и, +\\ -а-к а значит, найденная перестановка л является оптимальной.

ШагЗ. Предположим, что Sh S2,..., Snne имеют системы различных представителей, как в рассматриваемом примере. Тогда нарушается условие теоремы Ф. Холла, т. е. существуют -V, ,5. , .. .V. такие, что S, kjSj u.., <k. В нашем примере

-Si u kj S$ <j 1S4J = 2 < 4. Перейдем к новым значениям и* и у| , полагая

И* = И, -1, Д = И, -1,..., ы* = ; -1 и l 2 2 *

если индекс

Остальные щ и vy остаются без изменений. Обратимся к нашему примеру. На рис. 6.54 показаны новые значения переменных и* и v *.

Рис. 6.55. Матрица совпадений для новых значений и* и

При такой замене переменных не нарушается основное условие щ + V) > aipVi,j = 1, и. Действительно, возможны два случая: 1.7 е^и^и.-.и^тогдаи* ч-v* = (м, -I) + (Vj +1) =щ +Vj >ау.

2. j <г Sj и5 и...и S , а значит, v* --v и + > или

U! + Vj>>a,+ 1. Отсюда и* +v* =( , -l)+vy >atj +1-1 =ау.

Обозначим \Sj KjSjU...KjSik I =t <k, тогда новая сумма (6.14.2)

Сумма уменьшилась на к - t. Если теперь перейти к шагу 2, то в случае существования различных представителей для новых значений и* nv) , задача будет решена, в противном случае шаги 2 и 3 алгоритма продолжаем. Так как каждое повторение шагов алгоритма приводит к уменьшению суммы (6.14.2)

п п

на к - t едтгниц, следовательно, процесс закончится, что доказывает теорему.

7-2697

Замечание. При решении практических задач изменение переменных и и на 1 может затянуть получение ответа. Заметим, что алгоритм допускает изменение переменных и на любую величину, не нарушая при этом основного условия: Ui+Vj>a0Vi,j=l,n.

В рассматриваемом примере сумма уменьшилась на 2, так как $i и $2 и Щ и $4 = t = 2 и к = 4. Необходимо вернуться на шаг 2. Матрица совпадений примет вид на рис. 6.54, 6.55. Составим для нее систему множеств совпадений = {2},S2 = {2,3, 4}, S} = {1,4}, Проверим наличие системы различных представителей для данных множеств. Обращаясь к интерпретации системы различных представителей в терминах двудольного графа, надо проверить, что максимальное паросочетание равно 4 для графа Г= (¥\и¥ь U, Ф), где ¥t = {Sb S2, S3, SJ, V2 = [I, 2, 3, 4}, и связь вершин St -> {2}, S2 -* {2, 3, 4}, S2 -н> {1, 4}, SA {1, 3, 4}. Решая, можно установить, что существуют три таких паросочетания:

щ = {(Sh 2), (S2, 3), №, 1), (S4, 4)}, л2 = {(Sb 2), (S2, 3), (S2, 4), (54) 1)}, = {(Su 2), 4), 1), (S,i; 3)}. Таким образом, существуют три оптимальных назначения:

JT.1 2 3 4) (1 2 3 4) (I 2 3 4\ 1 ~{2 3 1 4/ 712 ~{2 3 4 1/ 713 ~{2 4 1 Ъ)

Ценность назначения составляем 12 + я2з + a3i 4 а44 =

6.15. Хроматические графы

Пусть = Х, U, Ф) - простой граф. Граф Г называется k-pac-

если существует такое разложение множества его

вершин Хна k непересекающихся подмножеств (компонент) Сь

таких, что к

Х=[]С С, =0 при 1Ф] (6.15.1)

и вершины в каждой компоненте независимы, т.е. ребра в /соединяют вершины только из разных компонент (рис. 6.56). Представление (6.15.1) называется k-раскраской графа Г. Вершины этого графа можно раскрасить k красками так, чтобы смежные вершины всегда были окрашены в разные цвета. Для этого достаточно вершины каждой компоненты покрасить своей краской.

6.15. Хроматические графы.

Наименьшее возможное число к - %(Г) компонент в разложении (6.15.1) называется хроматическим числом графа Г.

Рассмотрим несколько примеров хроматического разложения графов.

Утверждение 15.1. Полный граф Г = (X, U, Ф) на \Х ! = п вершинах имеет хроматическое число = Здесь каждая компонента С ; = 1,п разложения (6.15.1) состоит из одной вершины, CJ = 1, / = \,п.

Утверждение 15.2. ГрафГ= (X, U, Ф) содержит максимальный подграф (клику) из k вершин тогда и только когда, когда его хроматическое число равно k.

Доказательство. (=>) Пусть {хьх2,..., xk) е Xвершины максимального подграфа. Для разложения максимального подграфа требуется А: компонент Сь С2,..., СА таких, что е С,. Покажем, что этого числа компонент достаточно для разложения (6.15.1) всего графа Г. Пусть у е X - произвольная вершина и у £ {хЛ, х2,..., хк]. Среди* / = 1,ксуществует такая вершинах, е Ср которая несмежна с у, в противном случае существовал бы максимальный подграф из к + 1 вершины. Вершинуу включаем в компоненту Q. Следовательно, %(Г)= к.

(<=) Имеем %(Г) = к. Предположим, что максимальный подграф в Г содержит т вершин жт*к. Необходимое условие теоремы в этом случае утверждает: х(Г) = т, что противоречит условию.

Утверждение 15.3. Граф Г= (X, U, Ф) является двудольным тогда и только тогда, когда = 2.

Утверждение 15.4. Хроматическое число дерева равно 2, так как дерево является двудольным графом.

Теорема 6.15.1. Для числар(Г) вершинной независимости и хроматического числа х(Г графа Г= (X U, Ф), \Х = п выполняется соотношение

р(Г)хСГ)> п. (6.15.2)

Доказательство. В разложении (6.15.1) все компоненты являются независимыми. Из определения числа следует, что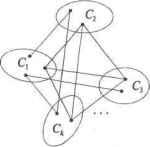

\(,\< Р(Г). Суммируя по всем компонентам, получим п=]Г\СЛ<кМП,гжк = уЛП.

Задача. Для графа / на рис.

6.57 найти разложение (6.15.1) I

и установить, что хроматиче-

. . , Рис. 6.57

ское число у\Г) = 3.

Задача. Пусть / - длина самой длинной простой цепи в графе Г. Показать, что Х(Г)< /+ 1.

Решение. Предположим, что х(Л >/+2 Тогда утверждение 15.2позволяет сделать заключение, что граф /содержит максимальный подграф (клику) из / + 2 вершин или более. Такой подграф содержит простой цикл из / + 2 ребер и простую цепь длиной / + 1. Это противоречит условию задачи, так как любая простая цепь графа не может превосходить длины /. Отсюда следует, что

6.16. Диаметр, радиус и центры графа

I. Пусть (Х, U, <Р) - конечный связный псевдограф. Обозначим через d(x, у) длину минимального маршрута между вершинами х, у Х. Величина = тах*/(х,у называется диамст-

ром графа.

П. Пусть х еХ- произвольная вершина графа. Величина r(x) =maxd(x,y) называется максимальным удалением в графе Г

от вершины х

III. Радиусом графа Г называется величина r(/)=minr(x).

хеХ

ТУ. Любая вершина z е Х, для которой Hz)= г{Г) называется центром графа.

Задача. Для графа Г на рис. 6.58 найти диаметр, радиус и все центры.

Решение. Диаметр d(r)=maxd(x,y)=

= 3. Г (Х|) = 3, /* i.Vj = 2, Г (Х3) = 3,

г (х4) = 2, г (х5) = 3, ге(х6) = 2. Следовательно, радиус графа г (Г) =minr(x) = 2.

Центры графа: х2, х4, х6.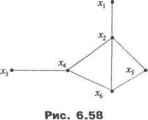

biases 7

Введение в теорию групп.

7.1. Определение группы

Определение. Группой называется непустое множество G с бинарной алгебраической операцией (будем называть умножением) такой, что выполняются следующие аксиомы:

1. va,fteG3ce Gab =с - замкнутость относительно операции .

2. ча Ь,се G а-ф-с) -(а-Ь)< - ассоциативность операции .

3. 5le eG Va eG е-а=а-е =а - существование единичного элемента е.

4. \Ja&G3\a-1 еС аа~1 аГ1 а = е - существование обратного элемента а .

Определение. Группа называется коммутативной, если выполняется аксиома коммутативности:

5. xafjeG a-b ~b-a- коммутативность операции .

Примеры групп

1. G = {/; \п е Z) - группа с операцией сложения чисел, где Z - множество целых чисел. Действительно, 0 - единица группы; и 1 = (-я) - обратный элемент к л е Gv

2. = \ п е - группа с операцией сложения чисел.

3. Gi = \2 \ л е Z}- группа с операцией умножения чисел.

4. GA - множество квадратных матриц порядка я, определитель которых не равен нулю, является группой с операцией умножения матриц.

5. - множество ортогональных матриц порядка п является группой с операцией умножения матриц.

6. 6( = {I, 1} - группа с операцией умножения чисел.

7. G, - множество рациональных чисел является группой относительно операций сложения и умножения (без

8. С?8 - множество вещественных чисел является группой относительно операций сложения и умножения (без нуля).

9, Сч = - множество подстановок (перестановок) является группой с операцией умножения подстановок (симметрическая группа 5 .. см. п.7.6).

Определение. #с G называется подгруппой группы G, если Н- группа относительно бинарной операции, определенной в G, т.е. для элементов Н выполняются аксиомы 1-4. Так, например, являются подгруппами: с 0, G= с G4, С- с 68.

Утверждение 7.1.1. Пусть М - подмножество группы Gm Va,be Мвыполняется ab 1 е М. Показать, что М - подгруппа. Данное условие можно рассматривать как характеристическое свойство группы.

Доказательство. Проверим выполнение аксиом группы.

1. Существование единичного элемента. Пусть а е М, тогда асГ1 е Мили е е М.

2. Существование обратного элемента. Пусть а е М и так как е е М, то е о 1 е Мили а~ е М.

3. Замкнутость. Пусть а, А е Jtf, тогда и b 1 е М Значит, и а (Г1)-1 е Л/или ab е М

7.2. Гомоморфизм групп

Определение. Гомоморфизмом группы Gx bG2 называется отображение /: Су -у Gi, сохраняющее операции: Va,beG{

f(a />) f(a)*f(b),где о - операция в группе - операция в группе G2. Если f- взаимно однозначное отображение, то/ называется изоморфизмом.

Свойства гомоморфизма

Свойство 1. Единичный элемент переходит в единичный. Пусть е{ е Cj - единица 6], тогда./}ti) = е2 е С2 - единица Действительно, VfleG,/(fl) =Aa)Aei) =Ае\)Аа), таккакДд) -Аае\) =Ао\Ае\) иЛа) = Ае\а) =Aei)A<1)- В группе Э!е> е G2 f(a) =jiu)e2 - evfia). Значит, Ae\) = e2.

Свойство 2. Обратный элемент переходит в обратный. Пусть а е Gj, тогдаАа~1) = (Да)) Действительно,) Да-1) =Аа~)Аа) = = е2, так как f(a) Да-1) =Aaa~l) =Aei) = Аа~1а) =Aa~l)fia), где М) = е2. В группе 3!(Дд)) 1бС2 (Да))-1 = (Д )Г!Д = е2. Следовательно, Аа ) - (Да))

Определение. Образом гомоморфизма/называется подмножество

Im/= {а2 е G2 \ Зя, е GY а2 =f(ax)} с G2.

- Определение. Ядром гомоморфизма/называется подмножество

Кет/= {а е(а,) = е2 s GV с G,.

Утверждение 7.2.1.Im/с 62 - подгруппа.

Доказательство. Проверим все свойства (аксиомы) группы.

1. Замкнутость. Va2,62e Im/ la *i е Gj /(а1)=а2л/ф1) = Ь2. Тогда a2i2 = /(ai)/ (&i) =f(aA) e Im/

2. Существование единичного элемента. Так как е2 = /(et)e Im/

3. Существование обратного элемента. Va2 е Im/ 3 3 е Gj /(oj) = % Тогда и a2! =(/( ! )) 1 =/(flf1)eIm/.

Утверждение Z2.2. Kler/r: Gx - подгруппа.

Доказательство. Проверим все свойства (аксиомы) группы.

1. Замкнутость. Vej.&j е Кег/ ДвД) =f{al)f{bfr е2е2 = е2. Следовательно, fljij е Кег/

2. Существование единичного элемента. Так как/( ,) = е2, значит, б! е Кег/

3. Существование обратного элемента.

Vfl,e Ker (V) = (/(ai)) 1 =е~г =е2, откуда а;1 еКег/.

7.3. Смежные классы

Определение. Пусть Н={е, hu h2,..., hm x} - подгруппа группы G. Множество gH= {ge,ghugh2,..., gh}, полученное умножением элементов Н слева на элемент g G, называется левым смежным классом группы G по подгруппе Н.

Лемма 7.3.1. Пусть Я - подгруппа группы G, тогда VА е Н пН=Н.

Доказательство. Пусть Н- {е, /г Л ..., Л,ПД. V/? е Н hhk е Н

- замкнутость подгруппы, значит ЛЯс Я. С другой стороны, \fhk е Hhk = ehk = (hh~l)hk = h(h~lhk) е ЛЯ, откуда Яс ЛЯ. Таким образом, V/ie Я /г#= Я.

тТелша 7.J.2. Пусть Я - подгруппа группы G. Если gxHrsg2H 0, то£1/;Г=г1-Т£,где£1 £2е G.

Доказательство. Пусть t в gxH n g2Н, тогда Щь h2 е Я такие, что t = gxhx = g2h2. Рассмотрим левый смежный класс Ш= (gxhx)H= = = откуда

Лемма 7.3.3. Пусть Я - подгруппа группы G, тогдаVg еб \gH\ = W\.

Доказательство. Для доказательства достаточно показать, что все элементы в различные. Пусть Щ * h2 е Я такие, что ghx = gh2. Тогда g i(ghx)=g l(gh2)vum (g~lg)hx= (g g,откуда

= что противоречит предположению.

Лемма 7.3.4. Группа распадается на непересекающиеся левые смежные классы по подгруппе Я, т.е. G =gxH\jg2Hvj... и у., , где всеgx, g2,..., gs - различные; g,Hr\gjh = 0, если ft ft. Доказательство. Пусть G ={g ,...,gk }. Ясно, что

G =gk H \jgk Hu...KjgkH. Воспользовавшись леммой 7.3.2иуда-лив совпадающие левые смежные классы из последнего разложения, получим искомое разложение группы G = gxHu g2Hgjl.

Теорема 7.3.1Лагранжа. Порядок конечной группы G кратен порядку любой из ее подгрупп Яи \G \ = Я| \G: Я|, где G: Н\ - целое число, называется индексом подгруппы Яв группе G. Доказательство. Лемма 7.3.4 позволяет записать разложение

группы G=gxH*u g2HKj...vj gsH,vr$ gjHn gtH = 0при ft*ft. Из леммы 7.3.3имеем Vg, g,jH = тогда Gl = \gxH\j g2Hu...u gsH= = \gxH\ + \g2ff\ + ... +)gfl\=s H. Следовательно, <5 = Я| \G:H\, где G: H\=s.

Определение. Пусть G - группа. Порядком элемента g е G (g*e) называется наименьшее целое Этакое, что£* = е.

Утверждение 7.3.1. Пусть G - группа и g е G - произвольный элемент порядка k. Тогда множество = называется циклической подгруппой, a g есть образующий ее элемент.

Утверждение 7.3.2. Порядок группы G \ кратен порядку любого элементае G. (Следствие теоремы 7.3.1Лагранжа и утверждения 7.3.1).

Утверждение 7.3.3. Всякая циклическая группа коммутативна

(абелева).

Теорема 7.3.2. Всякая подгруппа циклической группы сама является циклической.

Доказательство. Пусть G - циклическая группа с образующим элементом£е йиЯс G - подгруппа. Предположим, что наименьшая положительная степень элемента g, содержащаяся в . есть. Покажем, что элемент i - образующий элемент подгруппы Н. Допустим, что в Я содержится элементу/, где / * О и /не делится на к. Пусть d = (I, к)- наибольший общий делитель, тогда существуют такие целые числа и и v, что к и+/ v =й(см. п. 8.1). Следовательно, подгруппа Яв этом случае должна содержать элемент^ = (S*)W = r+v- Таккак< к, то приходим к противоречию относительно выбора элемента. Таким образом, i - образующий элемент подгруппы Не (Я

Утверждение 7.3.4. Число образующих циклической группы G= {g, g2,..., g ~ e) равно значению функции Эйлера <р(л) - количество чисел из множества {1,2,..., л-1} взаимно простых с п. Доказательство. Пусты е {1,2,..., -1} и (r,n) = 1 - НОД (см. п.8.1), т.е. ran - взаимно простые. Если предположить, что наступит {£)к=£к =едля некоторого к < л, то г к = п /для некоторого /, так как п - порядок элемента. Из г к = п /следует, что п делит к, так как (г, и) = 1. Это противоречит предположению к<п. Следовательно, порядок элемента /1 = п.

Пусть теперь (г, п) =s и s > 1, т.е. r = s р л п = s q, где (p,q)= 1. Тогда (#0?= (£p)9=gSM= tf? = (g Y= (f = e, а значит порядок элемента 1 с/ < п. Действительно, порядок g* не меньше q, в противном случае имеем (gr)q= (£)к = е, где к < q, и rk = nt, так как п - порядок элемента g. Как и в первом случае, ш г - к - п- /, s р k = s q t, р к= q t следует, что qделит т.к. (р, q) - 1. Это противоречит предположению < q.

Определение. Подгруппа Я группы G называется нормальным делителем, если правые смежные классы совпадают с левыми: Vge G gH= Hg.

Утверждение 7.3.5. Множество смежных классов группы Gпо нормальному делителю Яявляется группой с операцией умножения смежных классов. Такая группа называется факторгруппой и обозначается G/H. Элементами этой группы являются смежные классы разложения группы G=g1Hu g2Hu... и^Янатепересекающиеся левые смежные классы, т.е. G/H= = {glH,g2H,...,gsH}.