(* Формирование S=S+{v> *) nS:=nS+l; 3[nS]:=v;

(* Формирование пересечения множеств *)

и

Intersection(v,kD,nD,kDw,nDw,D); {Dm Adj[v]}

(* Формирование начального Z=N нового уровня *) kZw:=kZ+nZ; nZw:=nNw;

for i:=l to nNw do ZlfcZw+i] : NfkNw+.i]; (* Исследование поддеревьев нового уровня *) Clique(kNw,nNw,kDw,nDw,kZw,nZw) ;

(* Формирование *)

nS:=nS-l;

Формирование

nD:=nD+l;

D[kD+nD]:=v;

end;

kN,nN, kD,nD, kZ,nZ :Integer; i,j :Integer; yes -.Boolean;

begin

Assign (f,Clique.in ) ; Reset (f); {Фай/ открыт для чтения) {Ввох списка смежности)

Read(f,m); {Количестве строк в списке)

Fst[l]:=0; (Указатель начала первой строки списка)

for i:=l to m do begin

Read(f,Vtx[i]); {Метка вершины)

Read(f,Nbrfi]); {Количестве вершин в списке)

for j:=l to Nbr[i] do Read(f,Adj[Fst[i]+j] ) ;

{Список смежных вершин) Fst[i+1]:=Fst[i]+Nbr[i]; {Указатель начала следующей

строки в

end;

Close (f);

Assign(f,Clique.out);

открыт для

Init(yes);

if not yes then begin

структура смежности

Close (f);

exit;

end;

[Формирование начальных множеств: S, D, N, /,} nS:=0; {S - пустое)

kD:=0; nD:=0; {t - пустое множество} kN:=0; nN:=m; {Ь - все вершины графа} for i:=l to m do N[i]

kZ:=0; n2:-m; {Z - для исследования доступны все вершины} for i:=l to m do Z[i]:=i;

выделение

клик графа(

Close (f) ; end.

Воспользуемся данной программой в качестве примера для решения следующей задачи.

Задача. Симпатичный прием. Генерал желает устроить свой юбилей с максимальным числом гостей из своих знакомых. Стремясь сделать юбилейный вечер приятным, он должен организовать все так, чтобы на нем присутствовали люди, щие друг другу. Для достижения цели ему придется находить максимальную клику графа своих знакомых. Этот граф устроен следующим образом. Вершины его - знакомые юбиляра. Две вершины смежные, если соответствующие знакомые симпатизируют друг другу. Нетрудно понять, что клика этого графа с максимальным числом вершин и представляет тот самый максимальный контингент приглашенных, который может позволить себе юбиляр. Симпатичный граф знакомых генерала представлен на рис. 6.34.

Рис. 6.34

Пример порождения клик графа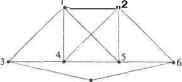

Для программы алгоритма 6.14 исходные данные структуры смежности этого графа задаются в текстовом файле

que.in. Структура (правило) заполнения файла совпадает с той, которая описана в примере поиска в глубину при расчете по программе алгоритма 6.2.

Данные файла Clique.inwra примера на рис. 6.34:

3 3 14 7 1 4 3 4 5 2

4 4 3 1 2 5 7 2 3 6

2 4 1 4 5 6

5 4 4 1 2 6

6 3 7 5 2

Результаты расчетов сохраняются в выходном файле Clique.out со следующей структурой:

6 5 2 6 7

4 5 2 1 4 3 1 3 7

Строки файла Clique.out - это номера вершин соответствующих клик симпатичного графа на рис.6.34. Отсюда видно, что в данном случае на вечер могут быть приглашены лишь четыре близких друга генерала.

6.12. Циклы, фундаментальные множества

В данном разделе рассматриваются алгоритмы решения задач, имеющих отношение к структуре циклов графа. Подобного рода задачи возникают при изучении вычислительных программ, в системах контроля при размыкании обратных связей и т. п. Рассмотрим остовное дерево Г0 = (X, Щ, Ф) графа Г= (X, U, Ф). Любое ребро, не принадлежащее U0, т. е. любое ребро из U\.порождает в точности один цикл при добавлении его к Такой цикл является элементом фундаментального множества циклов графа /относительно дерева Г0. Так как каждое остовное дерево графа Г включает \Х\- 1 ребро, в фундаментальном множестве циклов относительно любого остовного дерева графа / имеется \U\ -\Х + 1 циклов.

Полезность фундаментального множества циклов вытекает из

того факта, что это множество полностью определяет циклическую структуру графа: каждый цикл в графе может быть представлен комбинацией циклов из фундаментального множества. Пусть / {Сь С2,.. Cjt, m+1} - фундаментальное множество циклов, где каждый цикл С; является подмножеством ребер Цс U. Тогда любой цикл графа / можно записать в виде (С, Ф C, t)®...)Ф ), где символ Ф обозначает операцию симметрической разности, Cp<&Cq ={и \ u&CpuCqAU<tCpr\Cq).

Например, на рис. 6.35 показан граф и фундаментальное множество циклов, получающихся из выделенного жирной линией остовного дерева графа. Цикл графа (х{, х2, х5, х3) есть Ц © С3 ® С4 или цикл (хих2, хл, хъ) есть Сх Ф С2. Отметим, что в общем случае не каждая сумма циклов будет являться циклом

xl х!

Рис. 6.35. Граф, его остовное дерево и фундаментальное множество

При порождении фундаментального множества циклов удобно использовать метод поиска в глубину; он строит остовное дерево и каждое обратное ребро порождает цикл относительно этого дерева. Для того чтобы следить за ребрами дерева, используется поиск в глубину со стеком, в котором хранятся все текущие вершины пройденного пути в данный момент. Когда попадаем на обратное

ребро, обнаруженный цикл будет состоять из этого ребра и ребер,

соединяющих вершины из верха стека. Реализация рассмотренного подхода представлена в алгоритме 6.15, который строит фундаментальное множество циклов графа Г= (X, U, Ф).

Программная реализация поиска фундаментального множества циклов представлена в алгоритме 6.16.

Алгоритм 6.15. Фундаментальные циклы графа

for v Xdo Mark[v = 0; {Начальньн метки вершин) count - 0;

jC= 0; {Счетчик числа циклов) пС~ 0; {Вершит стека циклов) for v 6 Xdo ifMark[v] = 0 then begin

нС= nC+ 1;

С[пС] = v;

Cycle(v, 0); пС = пС- 1;

end;

Procedure Cycle(x, у) counts count + 1;

Mark[x] = count; {Вершина исследована)

for v s AdjfxJ do begin nC=nC+l;

C[n = v; {Вершит в стек) ifMark[v]= 0 then Cycle(v, x) else ifMark[vY Mark[x] л v Ф у then begin

jC=jC+ 1; {Обратноеребро (x, v), найден цикл) WriteCycle{v,C, nC); {Печать цикла)

end;

nC=nC- 1; {Удалитьисследованную вершину из стека) end;

Procedure Write Суcle{x, С, nQ printjC; {Печать номера цикла) repeat

print С]п(\: {Печать вершины из стека) nC = nC- 1; until С[пС\ =х;

Алгоритм 6.16. Программа поиска фундаментальных циклов

Program GraphCycle ; {Фундаментальные циклы графа}

uses CRT, DOS;

Const

nVortex-lOO; {Максимальное количество вершин) nAdjacent=1000; {Максимальная длина списка смежности)

TypeVertex=arrayi 1 , .nVertex] of Integer; TypeAdjacent=array [1. .nAdjacent] of Integer;

end;

end.

графа

:Text; :Integer; :Integer;

Текстовый файл ) { Количество вершин } { Количество вершин в стеке циклов)

6,12. Циклы, фундаментальные множества циклов.

Adj :TypeAdjacent;

Fst :TypeVertex; {

Nbr :TypeVertex; {

Vtx :TypeVertex; {

Mark :TypeVertex; )

С :TypeVertex; {

В -.TypeVertex; {

jC : Integer; {

count:Integer; {

{ Список смежности графа } Указатели вершин списка смежности) Количество вершин в списке смежности }

Список вершин графа }

[ Номера компонент для вершин графа)

Стек выделения циклов графа } ; Признаки основных и обратных ребер прохода в глубину }

Счетчик числа циклов } Счетчик меток вершин }

Procedure Init( var yes :Boolean );

{ Переназначение меток вершин }

{ их порядковыми номерами в списке смежности } { yes - признак правильной структуры списка смежности } Var

i,j,m :Integer;

begin

for i:=l to n do

for j:=l to Nbr[i] do begin yes:=FALSE; for m:=l to n do

if Adj[Fst[i]+j]=Vtx[m] then begin yes:=TRUE; Adj[Fst[i]+j]:=m; break-end;

if not yes then exit; end;

end;

Procedure x:Integer; var С:TypeVertex;

цикла из

begin

Write (f,jC,)); repeat

Write(f,Vtx[C[nC] ] :3) ;

nC:=nC-l; until C{nC>=x? Writeln(f);

end;

Procedure

i,v -.Integer;

begin

6.13.1. Листы

Определение. Пусть Г= (X, U, Ф) - неориентированный граф. Ребро и = (а, Ъ) е называется циклическим ребром, если оно принадлежит некоторому циклу. Петля является циклическим

ребром. Никакое концевое ребро (инцидентное висячей вершине) не может быть циклическим. Например, дерево не имеет циклических ребер, и, обратно, связный граф без циклических ребер является деревом.

Определение. Ребро и = (х, у) s С/называется разделяющим ребром (или мостом, или разрезающим ребром) в Г, если в графе Т, получающемся после удаления ребра и, вершины х и у не связаны. Тогда граф Г можно представить как объединение графов

Т=Г1Г2, (6.13,1)

где 1\ с\ Г- = 0, и 1\ содержит х, содержит у.

Утверждение 6.13.1. Ребро и = (х, у) е Цявляегсяразделяющим тогда и только тогда, когда оно не является

Доказательство. (=>) Допустим, что разделяющее ребро иявля-ется циклическим. Тогда после его удаления вершины х и у останутся связанными, а значит, разложение невозможно, что противоречит условию: и - разделяющее ребро. (<=) Теперь и = (х, у) - не циклическое ребро, т.е. не существует цепей, соединяющих х и у и не содержащих и. Отсюда и - разделяющее ребро.

Определение. Будем говорить, что две вершины их цикличе-ски-реберно связаны, если существует такая последовательность простых циклов что е е и каждая пара соседних циклов имеет хотя бы одну общую вершину. Условно взаимное расположение вершин и циклов можно представлять так, как показано на рис. 6.36.

--~Щ-----.......------

Рис. 6.36. Вершины циклически-реберно связаны

Утверждение 6.13.2. Циклически-реберная связность определяет отношение эквивалентности (см. п.6.4) на множестве вершин графа Г- (X, U, Ф). На рис 6.37 показано разбиение /на компоненты связности.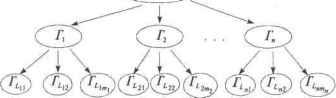

Рис. 6.37. Компоненты ГЩ) циклически-реберной связности графа. Компоненты r(Lk) связности графа. Компоненты ГЦ.ф s Г(Ц связаны мостами

Определение. Множество всех вершин, циклически-реберно связанных с данной вершиной х, называется листовьш множеством Цх). которому принадлежит х. Отметим, что листовое множество может состоять только из одной вершины х, тогда листовое множество называется особым. Далее будет показано, что это возможно тогда и только тогда, когда все ребра, инцидентные вершине х, являются петлями или разделяющими ребрами.

Определение. Подграф Г (L), определяемый листовым множеством L, называется листом.

Утверждение 6.13.3. Отметим следующие очевидные свойства листа

1. Граф Г(L) циклически замкнут, т.е. если какой-нибудь простой цикл С в /имеет общую вершину с L, то весь простой цикл С содержится в f(L).

2. Не может быть более одного ребра, связывающего два различных листовых множества Ly и L2, так как иначе эти ребра оказались бы циклическими и множества и должны были бы совпадать. Связывающие одиночные ребра различные листовые множества , и L2 являются мостами для графа. Ниже показано, что они будут являться и блоками, состоящими из одного ребра.

3. Все ребра в Г (I)являются циклическими. Пусть ребро (х, у) лежит ъГЩ. Покажем, что оно циклическое. Действительно, если, например, вершины х и у в L соединены ребром, тогда (х, у) циклическое по построению L. Если же х и у в L не соединены ребром, то, добавив данное ребро (х, у) к L,

получим цикл, так как вершины х, у связаны в L по построению. Отсюда следует, что ребро (х, у) циклическое. 4. По определению граф £(£ связный. Из предьщущего пункта следует, что маршрут в / (/.) соединяющий произвольные две его вершины, будет состоять исключительно из циклических ребер.

6.13.2. Блоки

Определение. Пусть (X, U, Ф) - неориентированный граф. Два ребра и, v e С/называются сильно циклически связанными, если существует такая последовательность простых циклов С- ..., С\, что и e С v e и любая пара соседних циклов С/+1 имеет, по крайней мере, одно общее ребро. Условно взаимное расположение ребер и циклов можно представлять так, как показано на рис. 6.38.

О

Рис. 6.38. Сильно циклически связанные ребра v

Определение. Множество всех ребер, сильно циклически связанных с ребром и е U, образует некоторую часть графа P(Lb), называемую блоком, определяемым ребром и. Множество вершин L этого графа называется блоковым множеством, определяемым ребром и. Блок является связным графом и может состоять из единственного ребра.

Лемма 6.13.1. Два ребра сильно циклически связаны тогда и только тогда, когда существует простой цикл, содержащий оба эти ребра. Справедливость данного утверждения следует непосредственно из структуры сильно циклической связанности ребер (рис. 6.38).

Лемма 6.13.2. Если Р(х, у) - простая цепь, связывающая две различные вершиных, у е Lb блокового множества, то все ребра цепи Р(х, у) принадлежат блоку Г(ЬЬ). Доказательство. Если предположить, что утверждение леммы

не выполняется, то существует участок цепи Р(х, у), ребра которого не принадлежат данному блоку Г(ЬЬ). Не уменьшая общнос-

Рис. 6.39

ти, будем считать, что этим участком является исходная цепь Р(х, у). Таккакх, у Е Lb, то в блоке Г (Lb)существует простая цепь Q(x, у), связывающая х, у. Тогда объединение простых цепей Р(х, у) и Q(x, у) составит простой цикл. Согласно лемме 6.13.1, ребра этого цикла будут сильно циклически связаны, а значит, все ребра простой цепи Р(х, у) должны лежать в Г(ЬЬ), что противоречит предположению.

Утверждение 6.13.4. Из леммы 6.13.2 следует, что блокГ(14) является подграфом. Он циклически сильно замкнут, в том смысле, что если простой цикл С имеет хотя

бы две вершины, общие с Lb, то все ребра цепи С принадлежат Г{ЬЬ). Поэтому два различных блока могут иметь не более одной общей вершины (рис. 6.39). В противном случае блоки должны совпадать.

Утверждение 6.13.5. Из определения блокового множества!* следует, что все его вершины являются циклически-реберно связанными при условии, что число ребер в блоке Г(Ь ) более одного. Отсюда заключаем, что Lb с L, где L - листовое множество вершин Lb, и каждый лист Г(Ь) имеет непересекающееся по ребрам разложение

r(L)=\Jr(Lb) (6.13.2)

на семейство блоков.

Определение. В графе.Г= (X, U, Ф) вершинухв Хназываютряз-деляющей вершиной (разрезающей или точкой сочленения), если имеет место прямое по ребрам разложение (рис. 6.40)

Г= r(Fj) и Г(У2), V= Pi u V2, Vx n V2=x. (6.13.3)

Рис. 6.40

Прямое по ребрам разложение графа

Утверждение 6.13.6. Блок . . /. не имеет разделяющих вершин, так как все его вершины циклически-реберно связаны. На основании разложения (6.13.2) любого листа Г(Ь) на непересекающееся по ребрам разложение на блоки Г (Lb) и последнего утверждения, составление листа Г(Ь) из блоков Г (L ) может быть представлено кактусообразной фигурой, как на рис. 6.41,