
|
| |||
|
Разделы
Главная
Сапромат
Моделирование
Взаимодействие
Методы
Инновации
Индукция
Исследования
Факторизация
Частоты
Популярное
Как составляется проект слаботочных сетей?
Как защитить объект?
Слаботочные системы в проекте «Умный дом»
Какой дом надежнее: каркасный или брусовой?
Как правильно создавать слаботочные системы?
Что такое энергоэффективные дома?
|
Главная » Математика 1 2 3 4 ... 28 Б. Н. ИВАНОВ Практическая компьютерная реализация большого количества рассматриваемых задач потребовала включения в книгу специальных разделов дискретной математики, таких как представление абстрактных объектов, сортировка и поиск, порождение комбинаторных объектов. Однако увеличение объема материала пособия только лишь усилило многие вопросы, позволило уточнить их суть, а также придать общее звучание разделам курса, которые на первый взгляд никоим образом не связаны. Книгу можно рассматривать в качестве хорошего справочника методов и алгоритмов дискретной математики, широко используемых в разработках прикладного программного обеспечения. Уровень математической подготовки, требующийся для понимания материала книги, может меняться от главы к главе. Минимум необходимых познаний в программировании соответствует уровню первокурсника, уже научившегося писать довольно пространные программы. Необходимый уровень математического образования соответствует типичной подготовке студента, прослушавшего ряд основных математических курсов, таких как математический анализ, аналитическая геометрия, линейная алгебра. Учебное пособие ориентировано на семестровый лекционный курс, читаемый автором на механико-математическом факультете Дальневосточного государственного технического университета. Без сомнения, книга может составить хорошую основу курсов, примыкающих к дискретной математике, таких как информатика, алгоритмизация процессов, анализ вьгаислительньгх алгоритмов. Учебное пособие предназначено прежде всего для студентов специальности Прикладная математика , а также студентов других специальностей, изучающих дискретную математику и программирование. Книга будет полезна преподавателям, аспирантам и научным работникам, применяющим методы дискретной математики в прикладных задачах. Интерпретация. Если элемент а еА можно выбрать т способами, а элемент ЬеВ-п способами, то выбор элементах еА kjB можно осуществить т + п способами. Пусть ХЬХ2,...,Хк- попарно непересекающиеся множества, г Xj = 0, где / ?= j Тогда, оче- видно, выполняется равенство =11* 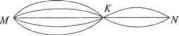 1.2. Правило прямого произведения Пусть А и В - конечные множества, А = т и В = п, тогда [Лх Б = т п. Интерпретация. Если элемент а еА можно выбрать т способами и если после каждого такого выбора элемент b еВ можно выбрать п способами, то выбор пары (а,Ь) еАх Явуказанном порядке можно осуществить А х Ц = т-п способами. В этом случае говорят, что выбор элементов множества А не зависит от способа выбора элементов множества В. Пусть теперь Хх,Х2,...,Хк- произвольные множества, Тогда \Х} xX2x...xXk\=\{(xl,x2,...,xk)\xi е X) J =U}j=n, -nr-nk. Задача. Найти число маршрутов из пункта М в пункт N через пункт К. Из Мв введут 5 дорог, из KB N-3 дороги. Решение. Введем два множества: S= {s s2, s3, s4, s5}-дороги из Me К, T= [tlt t2, г3}- дороги из KB N. Теперь дорогу из Me #мож-но представить парой (st р.где /= 1, 2, 3, 4, 5;у= 1, 2, 3. Значит, Sx Т - это множество всех дорог из Мв iV, количество которых равно iSx7=5-3=15. 1.3. Размещения с повторениями Задача формулируется следующим образом. Имеются предметы п различных видов Шу а2,..., ап. Из них составляют всевозможные расстановки длины к. Например, a2flia3fl3fl4fl3a2ai- Рас~ становка длины 8. Такие расстановки называются размещениями с повторениями из п по k (элементы одного вида могут повторяться). Найдем общее число расстановок, среди которых две расстановки считаются различными, если они отличаются друг от друга или видом входящих в них предметов, или порядком этих предметов. При составлении указанных расстановок длины k на каждое место можно поставить предмет любого вида. Рассмотрим множества Ху.Х^акж, что Х{ = Х2 = ... - Хк = {аъ а2,..., ап) . Тогда все размещения с повторениями составят множество ХххХ2 х...хХ к.Т1о правилу прямого произведения получаем, что общее число размещений с повторениями из л по к равно \Х1хХ2х...хХк\=пк. Задача. Найти количество всех гштизначных чисел. Решение. Введем пять множеств: А2=Аг=А\=А5= {0, 1,..., 9}, Ах = {1, 2,..., 9}. Тогда все пятизначные числа составят прямое произведение указанных множеств Д \А2 хЛ3 х Д, \А5. Согласно правилу прямого произведения, количество элементов в множестве А{ х А2 хА3 хД} х А5 равно 9 10 10 10 10 =90000. 1.4. Размещения без повторений Имеются различных предметов./,. <ь.....а„. Сколько из них можно составить расстановок длины к? Две расстановки считаются различными, если они отличаются видом входящих в них элементов или порядком их в расстановке. Такие расстановки называются размещениями без повторений, а их число обозначают При составлении данных расстановок на первое место можно поставить любой из имеющихся п предметов. На второе место теперь можно поставить только любой из п - 1 оставшихся. И, наконец, на к-е место - любой из п - к + 1 оставшихся предметов. По правилу прямого произведения получаем, что общее число размещений без повторений из л по А; равно Акп =п(п-\)...{п-к + \)=п\/{п-к)\. Напомним, что п\ =л(я-1)...1 и0!= 1. Задана. В хоккейном турнире участвуют 17 команд. Разыгрываются золотые, серебряные и бронзовые медали. Сколькими способами могут быть распределены медали? Решение. 17 команд претендуют на 3 места. Тогда тройку призеров можно выбрать способами А\п =17 16-15 = 4080. 1.5. Перестановки При составлении размещений без повторений из п по k мы получали расстановки, отличающиеся друг от друга либо составом, либо порядком элементов. Но если брать расстановки, которые включают все п элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие расстановки называются перестановками из п элементов, а их число обозначается Рп. Следовательно, число перестановок равно Р„ =А = п\. Перестановки я = (п^, л2,...,я ) элементов 1, 2,..., п записываютив {Л 1 и Л матричной форме п = , где верхняя строка -это по- V4 Щ ) рядковые номера 1.2,..., п позиций элементов в перестановке; нижняя строка - тотже набор чисел 1,2,..., я, взятых в каком-либо порядке; - номер элемента месте перестановки. Порядок столбцов в перестановках, записанных в матричной не является существенным, так как в этом случае номер позиции каждого элемента в перестановке указывается явно в верхней строке. Например, перестановка (3,2,4,1) из четырех элементов (12 3 4) Г3 1 4 2Л (2 14 3 может быть записана как Задача о ладьях. Сколькими способами можно расположить на шахматной доске 8 ладей, чтобы они не били друг друга? Решение. Условие не могли бить означает, что на каждой горизонтали и вертикали может стоять лишь одна ладья. Ввиду этого, каждому расположению ладей на доске соответствует переста- ( 1 2 8 *i т-* новка я = . Верхняя строка перестановки - это но- Vli -2 llsj мера горизонталей, нижняя - вертикалей, пересечение которых определяет положение ладей на доске. Следовательно, число расстановок равно числу перестановок = 8! из 8 элементов. 1.6. Сочетания В тех случаях, когда нас не интересует порядок элементов в а интересует лишь ее состав, то говорят о сочетаниях. Сочетаниями из п различных элементов по k называют все возможные расстановки длины k, образованные из этих элементов и отличающиеся друг от друга составом, но не порядком эле- ментов. Общее число сочетаний обозначают через С* или [Н Определим это число. Составим все сочетания из п по к. Затем переставим в каждом сочетании элементы всеми возможными способами. Теперь мы получили расстановки, отличающиеся либо составом, либо порядком, т.е. это все размещения без повторений из п по к. Их число равно Af. Учитывая, что каждое сочетание дает размещений, то по правилу произведения можно записать С* x£!=4f. Тогда С* = Я или С* =-~ , ч-. и к' к\{п-к)\ Задача о прямоугольниках. Сколько различных прямоугольников можно вырезать из клеток доски, размер которой т х л? Решение. Прямоугольник однозначно определяется положением его сторон. Горизонтальные стороны могут занимать любое из т + 1 положения. Тогда число способов их выбора равно С*+1. Вертикальные стороны можно выбрать С„2+1 способами. По правилу прямого произведения заключаем, что количество прямоугольников равно CfnA -С,;+1. 1.7. Сочетания с повторениями Имеются предметы п различных видов. Число элементов каждого вида неограниченно. Сколько существует расстановок длины к, если не принимать во внимание порядок элементов? Такие расстановки называют сочетаниями с повторениями, количество и обозначение которых следующее С„* =C£lk l =Ck v Выведем данную формулу. Пусть a, b,c,..., d- это исходные различные типы элементов, количество которых п. Рассмотрим произвольное сочетание с повторениями cbbcaccda...ddaccbbb из данных типов элементов. Так как порядок элементов в сочетаниях не учитывается, то расстановку можно записать и так: аа...а \ ЪЪ...Ъ \ сс...с \... \ dd...d, где элементы каждого из типов упорядочены и завершаются вертика-
Сочетания с повторениями льной чертой, за исключением последней серии элементов. Длина такой расстановки с учетом вертикальных линий составляет k + (п - \] =п + к- 1, где к - количество элементов в расстановке; п - 1 - число вертикальных линий. Очевидно, что любую такую расстановку можно задать выбором из п + к - 1 места п - 1 место для положений вертикальных линий. Это можно сделать СЙы способами. Промежуточные места между линиями заполняются соответствующими типами элементов. Задача. Трое ребят собрали в саду 63 яблока. Сколькими способами они могут их разделить между собой? Решение. Поставим в соответствие каждому делению яблок между ребятами сочетание с повторениями следующим способом. Типами элементов в нашем случае будут ребята. Таким образом, имеем три типа элементов а,Ь, с (п = 3), из которых предстоит составить все различные расстановки длины к = 63. Наличие в расстановке какого-либо из элементов а, Ъ, с отвечает принадлежности данного яблока соответствующему мальчику. Порядок элементов в такой расстановке не играет роли. При делении яблок между ребятами не важно, какое из них попадет тому или иному мальчику/Гогда число способов разделить яблоки между ребятами равно С363 = с£63 ! =С32+63 1 =2080. Задача. Найти количество целочисленных решений системы ху +х2+... +хп=к, k>Q,Xj>0,i= 1, 2,...,п;п >1. Решение. Рассмотрим следующую интерпретацию решения уравнения. Каждое значение х, = 1,г-н 1, + ... + представим как сумму единиц, количество которых Индекс у 1, отмечает ее принадлежность к разложению числа Таким образом, мы ввели п типов различных элементов значение каждого из них равно единице. Теперь любое решение исходного уравнения можно представить как сумму, составленную из к произвольных единиц множества {li, l2,-, U- Суммируя подобные единицы с одинаковыми индексами, можно составить соответствующие слагаемые решения исходного уравнения. Данное соответствие является взаимно однозначным, откуда и следует, что число решений системы равно числу сочетаний с повторениями Т^к (~>п-\ -Г^ *-л -Si+it-J -4i+A-r 1.8. Перестановки с повторениями, мультимножества Задача формулируется следующим образом. Имеются предме- ты k различных видов. Сколько существует перестановок из пх элементов первого типа, элементов второго типа и т. д., и* элементов Л:-го типа? Рассмотрим, например, мультимножество М= [а, а, а,Ь, Ь, с, d, d, d, d), в котором содержатся 3 элемента а, 2элемента Ь, 1 элемент с и 4 элемента d. Мультимножество - это то же самое, что и множество, но в нем могут содержаться одинаковые элементы. Повторения элементов можно указать и другим способом: М= {3-а.2Ь, \ с.4 d). Таким образом, искомые перестановки с повторениями - это перестановки элементов мультимножества. Если бы мы рассматривали все элементы множества М как различные, обозначив их то полу- чили бы 10! перестановок, но после отбрасывания индексов многие из них оказались бы одинаковыми. Фактически каждая перестановка множества М встретилась бы ровно поскольку в любой перестановке Миндексы при буквах а можно расставить 3! способами, при Ъ - 2! способами, при с - одним способом, а при d - соответственно 4! способами. Поэтому число перестановок множества Мравно . В применении к общему случаю те же рассуждения показывают, что число перестановок любого мультимножества (перестановки с повторениями) равно полиномиальному коэффициенту где я = пj + /?2 + ... + к - общее число элементов. Перестановки с повторениями имеют тесную связь с сочетаниями. Определим количество этих перестановок следующим образом. Из всех п мест перестановки место занимают элементы первого типа. Выбор мест для них можно сделать способами. Из оставшихся п - щ мест элементы второго типа занимают п2 места, которые можно выбрать С /п способами. Те же рассуждения показывают, что элементы А>го типа можно расположить в перестановке С* Л п п способами. Согласно правилу прямо- 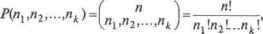 го произведения, число перестановок с повторениями равно **..... >-vw,=,v Задача. Сколько существует различныгх перестановок из букв слова Уссури ? * Решение. /(2 v.lj],!p,2c)----=180 2MMI-2! 1.9. Упорядоченные разбиения множества Подсчитаемчислоразбиенийконечного множества^ где \S\=n, на к различныгх подмножеств = S\j S\ и ... иЗк, попарно не пере- к секающихся, \%\ щ, i= 1, 2,..., к л =п . Последовательность щ последовательность подмножеств. При формировании упорядоченной Sb последовательности на первое место подмножество можно выбрать способами, на второе место подмножество можно выбрать из оставшихся п - щ элементов C l способами и т. д., на последнее место множество Sk можно выбрать из оставшихся пк у элементов п п способами. По правилу прямого произведения получаем, что общее число упорядоченных разбиений множества S на к подмножеств равно л ~~n-n1 п-п1-...-пк 1 и \ f и i1 1 .Jt......К что совпадает с числом перестановок с повторениями. Замечание 1. Установим взаимно однозначное соответствие между упорядоченными разбиениями множества и перестановками с повторениями. Каждой перестановке с повторениями можно поставить в соответствие упорядоченное разбиение множества номеров элементов S= {1, 2,..., п) в перестановке на подмножества где - множество номеров элементов /-го типа в перестановке. Очевидно, что данное соответствие между перестановками с повторениями и разбиениями является взаимно однозначным. Замечание 2. Упорядоченные разбиения множества S на попарно непересекающиеся подмножества S2 и ... и Sk = допускают интерпретацию в терминах корзин и шаров . Обозначим элементы исходного множества S \ = п шарами . Под разбиением исходного множества, теперь множества шаров, на различные S упорядоченные подмножества будем понимать разложение шаров по различным корзинам (упорядоченные шаров положить в корзину шаров положить в корзину и т. шаров положить в корзину где п1+п2 + ... +пк = п. Как установлено, число таких разложений С 1 С 2 С к ! п-п, п-п,-...-пи , л,1 равно Задача. В студенческой группе, состоящей из 25 человек, при выборе старосты за выдвинутую кандидатуру проголосовали 19 человек, против - 3, воздержались - 3. Сколькими способами может быть проведено такое голосование? Решение. Имеем три различные корзины: за , против , воздержались , в которые необходимо разложить 25 шаров, соответственно 19 - в первую, 3 - во вторую, 3 - в третью. Количество iy j 3 25! таких разложений определяется выражением C2J5 -Cg -С§ =у^~- 1.10. Неупорядоченные разбиения множества Подсчитаем, сколькими способами можно разбить множество S, где S = п, на подмножества, среди которых для каждого < == 1, 2;,.., п имеется > О подмножеств с элементами. Тогда верно, п что YJ-Щ =п. Данное разбиение позволяет представить исход-f=i ное множество следующим образом: 7=1 7=1 i=lj=l где .Уу попарно не пересекаются и =\Sf\-... = ISim \ =/для каждого / = 1,2,..., п. Порядок подмножеств в разбиении не является существенным. Так, например, разбиения множества 2, 3, 4, 5} вида 1.10. Неупорядоченные разбиения множества {1, 3}, {4}, {25}; {1, 3}, {25}, {4}; {25}, {1, 3}, {4}; {4}, {1, 3}, {25}; считаются одинаковыми. Обозначим число неупорядоченных разбиений множества S через N{mbm2,..., тп). Рассмотрим схему формирования упорядоченных разбиений для представления п =\-тх +2-т2+... + п-тп: Воспользуемся интерпретацией формирования упорядочен- ных разбиений как разложения различных шаров по различным пц + т2 +... +т корзинам так, что в каждую из т; корзину кладут шаров. Теперь откажемся от упорядоченности подмножеств в разбиении. Пусть все корзины имеют различное число шаров, такие корзины можно рассматривать как различные (они отличаются числом шаров). В этом случае упорядоченные и неупорядоченные разложения шаров совпадают. Пусть теперь в разложении существуют корзин с одинаковым количеством шаров. При упорядоченном разложении такие корзины рассматриваются как различные. Однако при неупорядоченном разложении обмен шарами таких корзин можно рассматривать как соответствующую перестановку указанных корзин, что не приводит к новым разложениям. Если количество корзин с одинаковым числом шаров равно то неупорядоченных разложений будет в меньше, чем упорядоченных. Тогда общее число неупорядоченных разбиений будет в т\\т2\...тп\ раз меньше, чем упорядоченных. Следовательно, Заметим еще раз, что если выполнено упорядоченное разбиение числа п на подмножества различной длины (мощности), то они совпадают с неупорядоченными разбиениями. В этом случае все Щ б{0,1}.  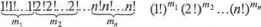 1 2 3 4 ... 28 |
|
| |||