Один из недостатков объектно-ориентированного моделирования заключается в том, что система не может предоставить все элементы, нужные для всех возможных приложений. Для каждой задачи может потребоваться свой набор элементов. Чтобы исключить этот недостаток, большинство систем объектно-ориентированного моделирования поддерживают какой-либо язык, на котором пользователь при необходимости может определять свои собственные элементы. После определения элемента необходимо задать параметры, указывающие его размер. Элементы, как и примитивы, могут быть разного размера, а задаются размеры параметрами в момент создания элемента. Создание элементов разного размера путем присваивания различных значений соответствующим параметрам является разновидностью параметрического моделирования.

Параметрическое моделирование

Параметрическое моделирование (parametric modeling) заключается в том, что конструктор определяет форму заданием геометрических ограничений и некоторых размерных параметров. Геометрические ограничения описывают отношения геометрических элементов. Примерами ограничений являются параллельность двух граней, компланарность двух ребер, касательность криволинейного ребра к , соседнему прямому и т. д. К размерным данным относятся не только заданные размеры формы, но и соотношения между размерами. Соотношения записываются конструктором в виде математических уравнений. Таким образом, параметрическое моделирование заключается в построении формы путем решения уравнений, выражающих геометрические ограничения, и уравнений, описывающих заданные размеры и соотношения между ними.

В параметрическом моделировании построение формы обычно осуществляется в приведенной ниже последовательности.

1. Строится грубый набросок плоской фигуры.

2. В интерактивном режиме вводятся геометрические ограничения и данные о размерах.

3. Строится плоская фигура, отвечающая ограничениям и требованиям к размерам.

4. Шаги 2 и 3 повторяются с изменением ограничений или размеров до тех пор, пока не будет получена нужная модель (рис. 5.22).

5. Объемное тело создается заметанием или вращением плоской фигуры. Толщина и угол поворота также могут стать размерными параметрами, что позволит при необходимости легко изменить созданную трехмерную форму.

Обратите внимание, что форма в параметрическом моделировании изменяется не непосредственно, а через использование геометрических ограничений и размерных соотношений. Поэтому конструктор может разработать множество альтернативных проектов, не заботясь о деталях, но сосредоточившись на функциональных аспектах.

Разновидности параметрического моделирования выделяются по методам решения уравнений, описывающих геометрические ограничения. Системы первого типа решают уравнения последовательно, а системы второго типа - одновременно. В первом случае форма тела зависит от порядка введения ограничений. Во

5.3. Системы твердотельного моделирования

втором случае одна и та же форма получается независимо от последовательности введения ограничений, но в случае их конфликта могут возникнуть проблемы.

Рис. 5.22. Изменение формы через ограничения

5.3.2. Структура данных

В предыдущем разделе мы описали разновидности функций моделирования, предоставляемых системами твердотельного моделирования. Мы знаем, что при создании объемного тела с применением этих функций в компьютере сохраняется его математическое описание. Каким образом и в каких форматах хранится эта информация, отражающая однозначное математическое описание объемных тел? В этом разделе мы расскажем о структурах данных, используемых для хранения математических описаний такого рода.

Структуры данных, используемые для описания объемных тел, обычно делятся на три типа в зависимости от того, какие тела ими описываются. Первая структура представляет собой дерево, описывающее историю применения булевских операций к примитивам. Журнал операций называется конструктивным представлением объемной геометрии (Constructive Solid Geometry - CSG representation). Дерево называется деревом CSG (GSG tree). Вторая структура содержит сведения о границах объема (вершинах, ребрах, гранях и их соединении друг с другом). Это представление называется граничным представлением (boundary representation - В-rep), а структура данных - структурой B-rep (B-rep data structure). Многие структуры В-rep строятся по-разному в зависимости от того, какой элемент считается основным при сохранении сведений о связности (см. далее). Третья структура представляет объем в виде комбинации элементарных объемов (например, кубов). Можно придумать множество моделей разложения, выбирая разные элементарные объемы, но ни одна из них не может точно описать объемное тело.

Дерево CSG

Вспомните, что дерево CSG содержит историю применения булевских операций к примитивам. Рассмотрим тело, изображенное на рис. 5.23, а. Его историю булевских операций можно представить в виде дерева так, как показано на рис. 5.23, б. Это дерево может быть представлено взаимосвязанными элементами данных (рис. 5.23, я). Элементы данных реализуются на языке С (листинг 5.1).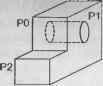

Нулевой указатель

Узел примитива

Узел примитива Узвп примитива

Рис. 5.23. Пример дерева CSG Листинг 5.1. Реализация структуры дерева CSG на языке С

struct primitive { int prim type: double posx. posy. pos z; double ori x. oriy. oriz: void *attribute:

/* тип примитива */ /положение экземпляра */ /* ориентация экземпляра */ /* значения размеров примитива */

Дерево CSG обладает следующими преимуществами:

□ структура данных проста, а их представление компактно, что облегчает обработку;

□ объемное тело, описываемое деревом CSG, всегда является корректным, то есть его внутренний объем однозначно отделен от внешнего. Примером не-

корректного объемного тела является тело с лишним ребром. Для него деление объема на внутренний и внешний вблизи вершины, к которой подходит это ребро, оказывается неоднозначным;

□ представление CSG всегда может быть преобразовано к соответствующему представлению B-Rep. Это позволяет взаимодействовать с программами, ори-ентированными на использование B-Rep;

□ параметрическое моделирование легко реализуется изменением параметров соответствующих примитивов (рис. 5.24).

Есть у этого дерева и недостатки:

□ поскольку дерево CSG хранит историю применения булевских операций, в процессе моделирования могут использоваться только они. Это требование жестко ограничивает диапазон моделируемых объектов. Более того, оно исключает использование удобных функций локального изменения, таких как поднятие и скругление;

□ для получения сведений о граничных поверхностях, их ребрах и связях между этими элементами из дерева CSG требуются сложные вычисления. К сожалению, сведения о границах нужны для множества приложений, в частности для отображения тел. Для того чтобы отобразить затушеванное изображение или чертеж объемного тела, нужно иметь информацию о гранях или вершинах этого тела (см. главу 3). Поэтому представление CSG является недостаточным для интерактивного отображения тел и манипулирования ими. Другой пример - расчет траектории движения фрезы с ЧПУ для обработки поверхностей тела. Для этой задачи нужны сведения о поверхностях, их ребрах и связности. Получить все эти сведения из дерева CSG очень непросто.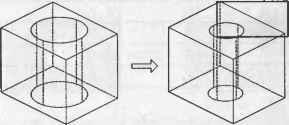

а б

Рис. 5.24. Изменение параметров тела

Из-за этих недостатков разработчики программ, основанных на представлении CSG, стараются добавить соответствующие сведения о границах. Такое комбинированное математическое представление называется гибридным и требует поддержания согласованности между двумя структурами данных.

Структура данных B-Rep

Границы объемных тел состоят из элементарных геометрических объектов: вершин, ребер и граней1. В структуре данных B-Rep хранятся все эти элементы вместе со сведениями о том, как они соединены друг с другом. Одна из простейших структур данных, если не самая простая, приведена в табл. 5.1. Структура данных представляет объемное тело, изображенное на рис. 5.25. В таблице граней хранится список ограничивающих ребер для каждой грани. Последовательность ребер для каждой грани дается обходом против часовой стрелки, если смотреть

1 Грань - часть граничной поверхности, граница которой состоит из криволинейных сегментов, при пересечении которых происходит существенное изменение вектора нормали к поверхности. Криволинейные сегменты, ограничивающие грань, называются ребрами. Точки, в которых встречаются соседние ребра, называются вершинами.

на тело снаружи. Благодаря тому что ребра хранятся согласованно, вместе с каждой гранью сохраняется информация о том, с какой стороны от нее находится внутренний объем тела. Другими словами, имея сведения о гранях, вы можете определить, где расположена конкретная точка: снаружи или внутри тела. Вершины, ребра и грани, изображенные на рис. 5.25, нумеруются системой геометрического моделирования в произвольном порядке в момент сохранения сведений из табл. 5.1.

Таблица 5.1. Три таблицы представления B-Rep

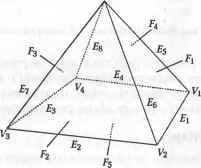Рис. 5.25. Объемное тело, сохраняемое в табл. 5.1

В каждой строке таблицы ребер хранятся вершины, находящиеся на концах соответствующего ребра, а в строках таблицы вершин хранятся координаты всех вершин. Эти координаты обычно определяются в модельной системе координат, связанной с данным телом. Если убрать отсюда таблицу граней, эту структуру данных можно будет использовать для хранения форм, созданных в системах каркасного моделирования. Структура данных для каркасной модели может использоваться в качестве базовой для систем автоматизированной разработки чертежей, если допустить указание двумерных координат для точек.

Структура данных B-Rep выглядит очень простой и компактной. Однако она не используется в развитых системах твердотельного моделирования из-за перечисленных ниже недостатков.

□ Структура данных B-Rep ориентирована на хранение плоских многогранников. Если потребуется сохранить данные о теле с криволинейными гранями и ребрами, строки таблиц граней и ребер придется изменять таким образом, чтобы в них можно было включить уравнения поверхности и кривой соответственно1. Уравнения для плоских граней сохранять не обязательно, поскольку плоские грани определяются находящимися на них вершинами.

□ Грань с внутренними и внешними границами (рис. 5.26, а) не может быть сохранена в таблице граней, поскольку для нее нужно два списка ребер вместо одного. Такие грани появляются, например, при моделировании объемных тел со сквозными отверстиями. Простым решением этой проблемы является добавление ребра, соединяющего внешнюю и внутреннюю границу (рис. 5.26, б). В этом случае два списка вершин могут быть объединены. Соединительное ребро называется мостиком или перемычкой (bridge edge) и попадает в список ребер в двух экземплярах.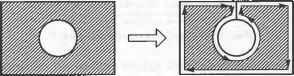

а б

Рис. 5.26. Поверхность с двумя границами и метод их обхода

□ Количество ребер у разных граней может быть различно (см. табл. 5.1). Более того, невозможно определить заранее количество столбцов (по одному на каждое ребро), которые потребуются для конкретной грани, поскольку это количество может меняться в процессе моделирования. Следовательно, количество столбцов должно сохраняться в виде переменной в момент объявления таблицы граней. Работа с таблицей переменного размера создает некоторые неудобства.

□ Получать сведения о связности непосредственно из данных, сохраненных в трех таблицах, может быть довольно утомительно. Представьте себе поиск двух граней с общим ребром в случае граничного представления тела в трех таблицах. Придется просмотреть всю таблицу граней, чтобы найти строки, в которых присутствует нужное ребро. Если нужно найти все ребра, соединяющиеся в конкретной вершине, опять-таки придется просматривать всю таблицу ребер. Легко видеть, что при больших размерах таблиц поиск в них становится крайне неэффективным.

1 Уравнения поверхностей и кривых, а также координаты вершин называют геометрическими данными, тогда как отношения между гранями, ребрами и вершинами называют топологическими данными. Данные в любой структуре B-Rep могут быть классифицированы либо как геометрические, либо как топологические.

Есть две распространенные структуры данных, которые позволяют избежать перечисленных проблем при сохранении граничного представления объемного тела. Это структура полуребер (half-edge data structure) и структура крыльевых ребер (winged-edge data structure).

Структура полуребер

В качестве средства для борьбы с таблицей граней переменного размера можно использовать двусвязный список1, в который помещаются сведения обо всех вершинах данной грани (рис. 5.27). Для каждой грани сохраняется указатель на первое ребро списка, а не весь список, тогда как в структуре каждого ребра имеются указатели на предыдущее и последующее ребро того же списка. В результате в таблице граней будет фиксированное число столбцов. Список ребер при этом всегда можно будет восстановить, переходя от одного ребра к другому по указателям (например, список ребер Е5, Е6 и £, для грани Fi). Грань F, может хранить указатель на Е6 или но список ребер всегда будет один и тот же.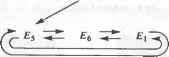

Рис. 5.27. Двусвязный список грани F,

Однако мы немедленно столкнемся с другой проблемой, когда перейдем к грани F2, которая имеет общее ребро Е6 с гранью F{ (рис. 5.25). Двусвязный список для грани F2 должен выглядеть так, как показано на рис. 5.28. По этому рисунку видно, что для ребра Е6 последующим является Е7, а предыдущим - Е2. Сохранив соответствующие указатели, мы изменим заданные ранее значения указателей, обеспечивавшие ребру Е6 место в списке ребер грани Fu то есть фактически разрушим список ребер грани Fv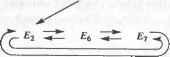

Рис. 5.28. Двусвязный список грани F2

Чтобы решить эту проблему, нужно разделить каждое из ребер на две половинки и использовать каждую из них в списке ребер той грани, к которой она относится. Деление ребра осуществляется таким образом, что его половинки оказываются противоположно направленными (рис. 5.29). Для каждой грани сохраняется двусвязный список полуребер, а не обычных ребер. Полуребра каждой грани собираются в список таким образом, чтобы направление каждого из них согласо-

Эту проблему можно решить и с односвязным списком. Мы выбрали двойной связный список, чтобы получить ту полуреберную структуру, которую предложил Мянтюля

вывал ось с направлением обхода границ грани: против часовой стрелки, если смотреть снаружи тела. В результате получаются двусвязные списки полуребер для граней F, и F2 (рис. 5.30). Теперь никаких проблем, приводящих к разрушению списка для ребра Fit не возникает.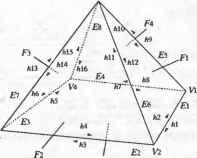

Рис. 5.29. Полуребра рассматриваемого тела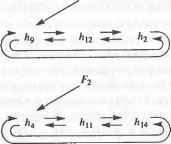

Рис. 5.30. Двусвязный список полуребер

Для описания граней с внутренними отверстиями без добавления избыточных соединительных ребер используются кольца. Кольцо (loop) - это список ребер, образующих замкнутую цепочку, так что любая грань ограничивается одним внешним кольцом и может ограничиваться внутренними1, определяющими отверстия. Теперь каждая грань может ссылаться на список полуребер через кольцо, а не непосредственно. Другими словами, для каждой грани хранится двусвязный список колец, а для каждого кольца хранится список полуребер. Это позволяет обрабатывать грани с любым количеством отверстий без добавления мостиков. На рис. 5.31 показано, как хранится в памяти грань с отверстиями при помощи колец. Обычно в структуру грани включается указатель на внешнее кольцо, а оно становится первым элементом двусвязного списка колец. У каждого кольца есть список полуребер, направление которых противоположно направлению внешнего кольца. Другими словами, полуребра отверстия помещаются в список

1 Внешнее кольцо и кольца отверстий называются также родительским (parent loop) и дочерними кольцами (child loop) соответственно.

Глава 5. Системы геометрического моделирования

в таком порядке, что их направления совпадают с направлением обхода отверстий по часовой стрелке, если смотреть снаружи тела. На рис. 5.31 полуребра кольца I, обходятся против часовой стрелки (это кольцо внешнее), а полуребра колец £2 и L3 - по часовой стрелке (эти кольца внутренние).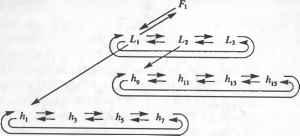

Рис. 5.31. Описание грани с отверстиями при помощи колец

Последовательность обхода полуребер отверстий противоположна последовательности обхода полуребер внешнего кольца для того, чтобы сохранить информацию о внутренней и внешней сторонах грани. Направления обхода выбраны таким образом, чтобы внутренняя часть грани всегда была по левую сторону при обходе любого кольца в соответствующем направлении.

Структура данных с полуребрами и кольцами имеет множество преимуществ перед структурой с таблицами вершин, ребер и граней. В структуре с полуребрами и кольцами можно сохранять данные о связности вершин, ребер и граней и по этим данным получать сведения о смежности. Мы уже показали, что получить такие данные по исходной простой таблице - задача непростая. Однако благодаря полуребрам и кольцам в структуре сохраняются сведения о связности вершин, ребер и граней, и тогда задача упрощается. Вершины, ребра и грани указывают на соответствующие полуребра и кольца, для которых сохраняются сведения о смежности. Чтобы обеспечить связь между ребром и его полуребрами, для каждого ребра сохраняются указатели на соответствующие полуребра, а для полуребер - указатели на родительские ребра. Аналогичным образом, для каждой вершины сохраняется указатель на одно из полуребер, исходящих из нее, а для каждого полуребра сохраняется указатель на его начальную вершину1. Для грани сохраняется указатель на внешнее кольцо, а для кольца - указатель на родительскую грань (см. рис. 5.31). Сведения о смежности колец и полуребер сохраняются естественным способом (каждое кольцо представляется в виде двусвязного списка полуребер).

Покажем, как можно получить информацию о смежности вершин и ребер из сохраненной структуры данных, чтобы продемонстрировать наличие в структуре всей необходимой информации. Например, попробуем найти все ребра, исходящие из вершины V] (рис. 5.32). Поиск начинается с полуребра, указатель на которое сохранен в вершине. Это может быть любое полуребро из тех, что соединены с данной вершиной. Обозначим его ht (см. рис. 5.32). Процедура поиска будет выглядеть следующим образом.

1 Вершина полуребра считается начальной или конечной в соответствии с направлением этого полуребра.

5.3. Системы твердотельного иидош^ичоп

1. Если вершина V\ является начальной вершиной h, (в нашем случае так и есть), то выбирается полуребро, предшествующее hi (prev h1), а его родительское ребро оказывается одним из нужных нам ребер, соединенных с Vi. Теперь место hi занимает сопряженное полуребро prey h1 (которое мы обозначаем new h1) и шаг 1 повторяется. Если V~i - конечная вершина hu выбирается полуребро, следующее за hi, а его родительское ребро считается одним из подходящих к вершине. Затем вместо hi берется полуребро, сопряженное со следовавшим за hi, и шаг 1 повторяется с полуребром new h1.

2. Процесс повторяется до тех пор, пока не будет достигнуто полуребро, сопряженное с исходным hi.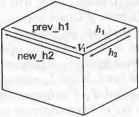

Рис. 5.32. Получение данных о смежности ребер и вершин

Реализация структуры данных полуребер представлена в приложении А. Структуру данных, используемую в системе твердотельного моделирования GWB, разработанной Мянтюля [106], демонстрирует листинг А.1. В книге [106] рассказывается о некоторых дополнительных указателях. В некоторых случаях оказывается выгоднее сохранить избыточные указатели, чем вычислять их заново, особенно если выполнять это пришлось бы часто. Количество и назначение избыточных указателей должны планироваться в процессе проектирования структуры данных. Реализация процедуры поиска всех ребер, исходящих из конкретной вершины, на предлагаемой структуре данных, представлена в листинге А.2.

Структура крыльевых ребер

Структура полуребер представляет собой список граней, каждой из которых соответствует двусвязный список ребер. В этой структуре главная роль в описании объемного тела отводится граням. В структуре крыльевых ребер (winged-edge data structure) главная роль, напротив, отводится ребрам. Для каждого ребра сохраняется список граней, которым оно принадлежит, ребер, с которыми оно имеет общие вершины, и вершин на его концах. Список ребер для каждой грани не сохраняется в структуре в явном виде, поскольку он может быть получен анализом любого ребра грани и соседних с ним ребер. Проблема неопределенности количества ребер у граней решается без введения связных списков и, следовательно, полуребер. Последнее объясняет, почему сведения о связности вершин, ребер и граней сохраняются в структуре данных в явном виде. В структуре полуребер связность неявно описывалась самими полуребрами. Мы уже отметили некоторую часть сведений о связности: для каждого ребра сохраняются грани, которым оно принадлежит, соседние ребра и конечные вершины.

Структура крыльевых ребер впервые была предложена Бомгартом [И]. Брейд расширил ее, добавив поддержку тел со сквозными отверстиями посредством использования колец [23].

Определим структуру крыльевых ребер для фигуры, изображенной на рис. 5.33. Ребро Et является смежным с четырьмя другими ребрами: Е2, Е3, Е4 и Е5, каждое из которых содержит одну из двух вершин ребра Если рассматривать ребро Е1 как фюзеляж самолета, четыре ребра Е2, Е3, ЕА и Е5 будут его крыльями. Эти четыре смежных ребра называются крыльевыми ребрами £,. Каждое из них должно быть сохранено под отдельным именем с информацией о положении этого ребра относительно Е{. Именуются крыльевые ребра так. Вначале £4 назначается определенное направление (рис. 5.33). Здесь ребро направлено от вершины V4 к вершине V2. Затем следует представить себе, что вы лежите вдоль ребра £t так, что голова направлена к V2 (а тело, разумеется, находится снаружи объема). Вытяните руки и ноги так, как если бы вы летели. Левая рука коснется ребра Е2, правая рука - ребра Е3, левая нога - ребра £4, правая нога - ребра Е5. Поэтому ребро Е2 называют ребром левой руки, Е3 - ребром правой руки, Е4 - ребром левой ноги, £5 - ребром правой ноги. Если £4 направить в противоположную сторону, £5 будет ребром левой руки, Е4 - ребром правой руки, Е3 - ребром левой ноги и Е2 - ребром правой ноги. Направление каждого ребра устанавливается произвольно в момент создания объемного тела и сохранения его структуры крыльевых ребер.

Помимо связности ребер в терминах крыльевых ребер необходимо также описать связность граней и ребер. Поэтому для каждого ребра сохраняются указатели на две грани, которым оно принадлежит. Например, для ребра £, на рис. 5.33 сохраняются указатели на ребра Fx и F2 (левое и правое соответственно). Названия ребер определяются направлением £,. Граням присваиваются разные названия по той же схеме, по которой они присваиваются крыльевым ребрам. Брейд предложил использовать кольца для сохранения сведений о телах со сквозными отверстиями в структуре крыльевых ребер. Связь между гранью и ее ребрами задается неявно при помощи колец. Каждое ребро хранит указатель на свое левое и правое кольца, а не на левую и правую грань. Например, на рис. 5.33 ребро Ех хранит указатель на Lx как на левое кольцо и на Ь2 как на правое кольцо. Если направление £, изменить на противоположное, названия колец также изменятся. Кольца содержат указатели на все ребра, которые к ним относятся. Это дает возможность получить список всех ребер одного кольца. Процедура аналогична получению списка полуребер начиная с любого произвольного полуребра, на которое имеется указатель в кольце.

Теперь рассмотрим описание связности ребер и вершин. Вспомните, что у каждого ребра на концах находятся вершины. Эти вершины сохраняются под именами предыдущая вершина (previous vertex или tail vertex) и последующая вершина (next vertex или head vertex), поскольку все ребра имеют направления. На рис. 5.33 Vi является предыдущей вершиной для £ a V2 - последующей. Сохраняются не только указатели на вершины в структурах ребер, но и указатели на ребра в структурах вершин - по одному ребру для каждой вершины. Это позволяет выделить ребро, начиная с которого перечисляются все ребра, сходящиеся в одной вершине. При реализации функций моделирования, в особенности содержащих

операторы Эйлера (см. раздел 5.3.3), прихолится часто просматривать списки ребер, сходящихся в одной вершине.

Описанные способы сохранения информации о связности вершин, ребер и граней иллюстрирует рис. 5.34.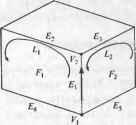

Рис. 5.33. Определение структуры крыльевых ребер

Вершина Правое кольцо

Следующая вершина Ребро левой руки Ребро правой руки

Кольцо у/* Левое кольцо -*-Ребро-

Ребро I \ Ре6р0

Ребро левой ноги Ребро правой ноги

Предыдущая вершина Рис. 5-34. Связность вершин, ребер и граней

Помимо описанных связей сохраняются также связи между гранями и их кольцами, как в структуре данных полуребер. А именно, для каждой п^ани сохраняется указатель на ее внешнее кольцо, а для внешнего кольца сохраняется указатель на кольцо отверстия, если в данной грани оно есть. Кольцо отверстия может указывать на другое кольцо отверстия, если в грани отверстий несколько; в противном случае оно указывает обратно на внешнее кольцо (рис. 5.35). Кроме того, для каждого кольца сохраняется указатель па его родительскую грань. Заметьте, что здесь используется односвязный список, а не двусвязный, как на рис. 5.30. Выбор односвязного или двусвязного списка определяется тем, что считается более важным - эффективность обращения к данным или компактность структуры.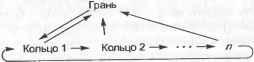

Рис. 5.35. Связи между гранью и ее кольцами

Пример реализации структуры данных крыльевых ребер на языке С демонстрирует листинг Б.1 в приложении Б. Эта структура данных используется в системе твердотельного моделирования SNUMOD, разработанной в Сеульском государ-

ственном университете в Корее. В листинге присутствует новый элемент - оболочка (shell). Оболочка - это трехмерное расширение кольца, то есть список граней, образующих замкнутый объем. Обычно в объемном теле может быть только одна оболочка, если в нем нет полостей. Полость в объемном теле - это трехмерное расширение кольца отверстия в грани. Следовательно, концепция оболочки позволяет описывать объемные тела с полостями точно так же, как концепция кольца отверстия позволяет описывать грань с отверстиями.

Структура декомпозиционной модели

Объемная модель может быть приближенно представлена в виде совокупности простых тел, например кубов. Такая модель называется декомпозиционной (decomposition model). Можно предложить много декомпозиционных моделей описания одного и того же тела. Модель включает в себя простейшее тело и метод объединения в совокупность. К типичным декомпозиционным моделям с соответствующими структурами данных относятся воксельное представление, представление октантного дерева и ячеечное представление.

Воксельное представление

Воксельное представление (voxel representation) объемного тела - это просто трехмерный аналог растрового представления плоской фигуры. Чтобы рассказать о воксельном представлении, нам придется вспомнить процедуру получения растрового представления или растрового изображения. Растровое изображение двумерного объекта формируется следующим образом. Сначала создается квадрат, размер которого соответствует интересующей нас области двумерного пространства. Затем квадрат делится на много маленьких квадратиков путем нанесения на него линий сетки. Расстояние между линиями сетки определяется желаемой точностью растрового представления. Другими словами, если это расстояние будет очень маленьким, то растровое изображение будет очень точно воспроизводить форму исходного двумерного объекта. В противном случае получится лишь грубое приближение. Квадрат, содержащий много маленьких квадратиков, представляется в компьютере в виде двумерного массива, количество элементов в котором совпадает с количеством квадратиков. Наконец, большой квадрат накладывается на двумерный объект, и элементы массива, соответствующие квадратикам, находящимся над объектом, получают значение 1, а остальные элементы получают значение 0. Получившийся массив нулей и единиц становится растровым представлением двумерного объекта.

Воксельное представление объемного тела получается при помощи той же процедуры, что и растровое представление. Однако начинается она не с большого квадрата и маленьких квадратиков, а с большого куба и маленьких кубиков, называемых вокселами1. Деление на вокселы осуществляется сеткой плоскостей, расположенных на равном расстоянии друг от друга перпендикулярно осям х, у и 2. Исходный куб представляется в виде трехмерного массива, количество элементов которого совпадает с количеством кубиков, и каждому элементу массива присваивается значение 0 или 1 в зависимости от положения элемента в теле.

ооксел - это трехмерный аналог пиксела. Последние четыре буквы названия взяты от слова пиксел (pixel), а первые две - от слова объем (volume).

Несмотря на то что эта процедура практически идентична процедуре формирования растра, проверка пересечения тела и кубика требует больших вычислений, чем аналогичная двумерная задача1. Воксельное представление объемного тела, имеющего форму бублика, демонстрирует рис. 5.36.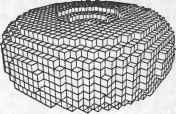

Рис. 5.36. Визуализация вексельного представления (благодаря любезности ACM, Inc.)

Воксельное представление обладает следующими преимуществами.

□ Воксельное представление позволяет точно или по крайней мере приблизительно описать объемное тело совершенно произвольной формы. Например, модели человеческих костей и органов часто являются вексельными представлениями данных цифровой томографии. Моделировать такие формы при помощи обычных функций очень сложно. Даже применение сложных процедур, описанных в разделе 5.3.1, все равно не позволяет построить точную модель.

□ Воксельное представление позволяет с легкостью рассчитывать такие параметры объемного тела, как масса и моменты инерции. Расчет осуществляется путем суммирования параметров отдельных вокселов. Также легко получить результат булевской операции. Вообще говоря, для этого достаточно всего лишь применить булевскую операцию к целочисленным значениям соответствующих вокселов двух тел.

□ Хотя воксельное представление предназначено для описания объемного тела в пространстве, оно автоматически описывает и пространство вне тела. Поэтому оно удобно для расчета объема полых структур. Применимо оно и для расчета траекторий движения роботов, уклоняющихся от препятствий, поскольку воксельное представление препятствий содержит и информацию о свободном пространстве.

Есть у воксельного представления и некоторые недостатки.

□ Объем памяти, требуемый для хранения воксельного представления тела, резко возрастает с уменьшением размеров вокселов. Размер вокселов опредм ляет точность приближения исходного тела, поэтому моделирование можетл потребовать предельного его снижения.

□ Воксельное представление по определению является приближенным описанием исходного тела. Поэтому систем твердотельного моделирования, в кото-j рых оно является основным математическим описанием объектов, довольно мало. Вокселы часто используются в качестве внешнего представления, по- вышающего эффективность вычислений.

Представление октантного дерева

Представление октантного дерева (octree representation) аналогично вексельному в том плане, что тело рассматривается как совокупность шестигранников (куб - это правильный шестигранник). Однако это представление предъявляет значительно менее серьезные требования к памяти благодаря иной схеме деления пространства. В воксельном представлении исходный куб делится сеткой плоскостей, находящихся на равном расстоянии друг от друга по осям X, у и z. В представлении октантного дерева исходный куб делится каждый раз на восемь равных кубов поперечными плоскостями (рис. 5.37, а). Объем маленького куба в восемь раз меньше объема исходного, отсюда и название представления. Более того, если кубики представить в виде узлов дерева, то от каждого узла будет отходить восемь ветвей (рис. 5.37, б). Такое дерево и называется октантным1 (octree). Если бы каждый кубик всегда делился на восемь меньших вне зависимости от формы моделируемого тела, то результат был бы полностью аналогичен воксельному представлению с кубиками постоянного размера. Однако в представлении октантного дерева некоторые кубики делятся на восемь частей, тогда как другие кубики того же уровня остаются целыми. Определяется это положением кубиков по отношению к представляемому телу.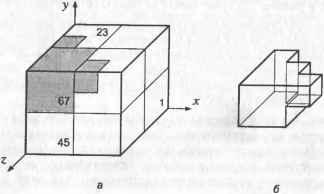

Рис. 5.37. Пример формирования октантного дерева

Аналогичное представление можно построить и для двумерного объекта, но в этом случае дерево будет называться квадрантным (quadtree).

Процедура построения представления октантного дерева выглядит следующим образом. Сначала создается шестигранник, в который моделируемое тело помещается целиком. Этот шестигранник называется корневым октантом (root octant). Затем корневой октант делится на восемь октантов, после чего анализируется их положение в пространстве по отношению к моделируемому телу. Если октант находится полностью внутри тела, он считается черным ; если снаружи - белым . Если же октант частично лежит внутри тела, а частично - снаружи, то он считается серым и делится на восемь октантов меньшего размера. Черные и белые октанты дальше не делятся. Процедура повторяется до тех пор, пока не будет достигнут заданный минимальный размер октанта После этого октанты, окрашенные в черный цвет, считаются относящимися к исходному телу1. На рис. 5.37, в показано октантное дерево для тела с рис. 5.37, б. Количество октантов, под которые приходится отводить память, много меньше количества во-кселов для тела того же объема, поскольку белые и черные октанты дальше не делятся. Октантное дерево с рис. 5.37, в хранится в компьютере в виде структуры данных. Реализация такой структуры на языке С показана в листинге 5.2, а процедура формирования октантного дерева на основе этой структуры данных приводится в листинге 5.3. Эта процедура представляет собой, по сути, запись на языке программирования описанных выше действий. Несмотря на относительно простой вид процедуры, подпрограмма classify(p.t) требует сложных геометрических вычислений, поскольку она определяет, где находится конкретный октант: внутри тела, снаружи его или на границе. Серые октанты преобразуются в черные после окончания процесса деления. Поэтому объем модели, полученной в результате применения этой процедуры, будет заведомо большим объема исходного тела.

Листинг 5.2. Структура данных для хранения октантного дерева

struct octreeroot

float float struct

octree

struct octree

char struct

octree

xmin, ymin. zrnin: xmax. ymax. zmax: *root:

/* гранииы пространства */ /* корень дерева */

code: /* цвет октанта: BtACK. WHITE. GREY */ *oct[8]: /* указатели на октанты */ /* отличны от нуля, если code==GREY */

Листинг 5.3. Процедура формирования октантного дерева

make tree(p. t. depth)

primitive *p: /* p - моделируемый примитив */

octree *t: /* t - узел дерева, то есть исходное дерево с одним серым узлом */

int depth: /* максимальная глубина рекурсии */

1 Серые октанты также могут быть включены в представление. Объем тела при этом оказывается большим действительного. Если же брать только черные октанты, объем полу чится заведомо меньшим действительного.

int i: switch(classify(p. t)) {

case WHITE:

t->code - WHITE:

break: case BLACK:

t->code - BLACK;

break: case GREY:

if (depth-O)

t->code - BLACK:

else {

subdivide(t):

for (i-0: i<B: 1++)

make tree(p.t->oct[i].depth-1):

break:

/* функция определения цвета узла дерева */ classify(...):

/* функция деления узла на восемь октантов */ subdivide..):

Ячеечное представление

Ячеечное представление (cell representation) - это еще один метод представления объемного тела в виде комбинации простых элементов, подобный воксельному представлению. Однако, как следует из названия представления, ячеечный метод не накладывает жестких ограничений на форму этих элементов. Практически любое объемное тело можно представить при помощи небольшого набора простых ячеек. Пример ячеечного представления представлен на рис. 5.38. Как видно из этого рисунка, формирование сетки конечных элементов для конечно-элементного анализа является частным случаем ячеечного представления.

Рис. 5.38. Пример ячеечного представления

5.3.3. Операторы Эйлера

Обратимся теперь к задачам, связанным с изменением структур данных, используемых в системах твердотельного моделирования. Эти задачи имеют особую важность, поскольку функции моделирования реализуются посредством служебных операций, обновляющих структуры данных.

Поскольку большинство систем твердотельного моделирования основаны на структуре данных B-Rep, мы рассмотрим операции, манипулирующие данными, организованными именно в виде структуры B-Rep. Вы уже знаете, что в структурах данных B-Rep хранятся такие топологические элементы, как оболочки, грани, кольца, ребра и вершины. Мы можем рассматривать операторы, работающие с такими элементами, то есть операторы создания ребра, удаления вершины и т. д. Если эти операторы использовать в реализации функций моделирования, сразу возникнут проблемы.

Попытка рассматривать топологический элемент отдельно от тех элементов, с которыми он связан, несет в себе внутреннее противоречие. К топологическим элементам применимо приведенное ниже равенство, которое называется формулой Эйлера-Пуанкаре [120, 23]:

v-e + f-h=2(s-p), (5.1)

где v - количество вершин, е - количество ребер, / - количество граней или внешних колец, h - количество колец отверстий, s - количество оболочек и р - количество сквозных проходов через отверстия в теле. Можно проверить это уравнение на фигуре, изображенной на рис. 5.39. Здесь v= 16,/= 10, h = 2, s= 1 и р = 1 (посчитайте самостоятельно). Подставив эти значения в уравнение (5.1), мы получим:

16-24 + 10-2=2(1-1).

то есть уравнение 5.1 оказывается верным. Из этого уравнения мы можем сделать вывод, что шесть топологических элементов не могут быть независимы одновременно. Независимость обеспечивается лишь для пяти из них.

Манипулирование топологическими элементами по отдельности оказывается малоэффективным, поскольку в большинстве случаев добавление или удаление элемента приводит к изменению состояния других элементов. Например, добавление диагонального ребра приводит к увеличению количества граней, поскольку исходная грань делится на две (рис. 5.40). Для достижения эффективности нужно иметь оператор, который самостоятельно заботился бы обо всех побочных эффектах этого рода.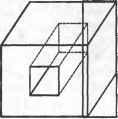

Рис. 5.30. Пример объемного тела

Рис. 5.40. Добавление ребра приводит к изменению грани

Итак, было бы удобно иметь операторы, которые манипулировали бы небольшими группами топологических элементов, а не каждым из них в отдельности. Поскольку в формуле (5.1) одновременно являются независимыми пять элементов, для увеличения или уменьшения количества любого из шести топологических

элементов из этого уравнения необходимо пять операторов. Таким образом, нам нужно определить не более пяти операторов. Полезно было бы определить их так, чтобы они одновременно изменяли такие элементы, которые часто меняются вместе, когда конструктор варьирует форму тела. Предсказать, какая именно группа топологических элементов будет изменяться наиболее часто, не так-то просто. Однако операторы должны включать топологические элементы, которые по меньшей мере удовлетворяют уравнению Эйлера-Пуанкаре. Например, нам подошел бы оператор, создающий ребро и вершину, поскольку он позволяет увеличить количество ребер и вершин на единицу, сохраняя истинность уравнения (5.1). Благодаря этому объемное тело, изначально являвшееся корректным, гарантированно останется таковым после изменения его топологии. Операторы, удовлетворяющие перечисленным выше требованиям, называются операторами Эйлера (Euler operators). Существует много разных наборов операторов Эйлера, и в каждой системе твердотельного моделирования используется свой собственный набор. Изменение, показанное на рис. 5.41, - пример применения оператора Эйлера, который называется Создать Ребро и Кольцо (Make and Edge and a Loop - MEL). Этот оператор увеличивает число колец, соединяя две вершины одного кольца новым ребром. Легко представить себе использование этого оператора для деления грани на две части перед поднятием одной из этих частей. На рис. 5.44 перечислены операторы Эйлера, часто используемые в этой книге.

Рис. 5.41. Операторы Эйлера

тве?тпЛ°ЖеНИИ В МЫ ПеРечислили операторы Эйлера, используемые в системе ерДОхельного моделирования SINUMOD, описали реализацию типичных

функций моделирования. Список операторов практически совпадает с предложенным Чийокурой [35]. Подробное описание операторов Эйлера и их реализации можно найти в работах [106, 35].

5.3.4. Булевские операторы

Из всех функций моделирования булевские операторы являются наиболее сложными с точки зрения реализации, однако они предоставляют наиболее широкие возможности пользователю системы моделирования. Как уже отмечалось, к булевским операциям относятся объединение, пересечение и разность объемных тел. Результат операции сохраняется в структуре данных, характерной для используемой системы твердотельного моделирования. Если эта система основана на дереве CSG или декомпозиционном представлении, результат булевской операции легко будет представить в той же структуре. Дерево CSG результата любой булевской операции получается простым комбинированием деревьев исходных тел при помощи соответствующей операции булевской алгебры. То же относится и к декомпозиционной модели: там булевские операции применяются к пространственным элементам тел. Например, воксельное представление результата булевской операции может быть получено применением соответствующей операции (побитовой булевской операции) к значениям вокселов двух тел, попадающих в одну и ту же точку пространства.

Если же система твердотельного моделирования использует структуру B-Rep, ситуация оказывается принципиально иной. В этом случае структуру B-Rep исходного тела приходится вычислять по структурам B-Rep исходных тел, к которым применяется булевская операция. Этот процесс называется вычислением границ (boundary evaluation).

Алгоритм вычисления границ был впервые предложен Реквичей и Велкером [132] под названием процесс вычисления и слияния границ (boundary evaluation and merging process) и впоследствии был усовершенствован Миллером [115]. Предлагаемый метод реализуется в три этапа. Для удобства иллюстрирования мы решили воспользоваться плоским рисунком (рис. 5.42), но тот же подход применим и к трехмерным телам. Сначала обозначим две грани (два тела в трехмерном случае), к которым должна быть применена булевская операция, буквами А и Б, а результат операции назовем буквой В (рис. 5.42, а). На первом этапе все ребра А и Б, а также ребра, получаемые пересечением этих граней, помещаются в единый пул ребер. Подмножеством пула ребер, очевидно, являются все ребра грани В. На втором этапе все ребра пула классифицируются по их положению относительно граней А и Б. Любое ребро может находиться, во-первых, внутри, на границе или снаружи грани и, во-вторых, внутри, на границе или снаружи грани Б (рис. 5.42, б). На третьем этапе ребра группируются по их относительному положению в соответствии с применяемой булевской операцией. Заметьте, что для операции А объединить с Б нужно отбросить все ребра, находящиеся внутри А и внутри Б (см. рис. 5.42, б). Аналогичным образом для операции А пересечь с Б отбрасываются ребра, лежащие вне А и вне Б . Собранные ребра формируют грань. Для этого в структуру заносятся все необходимые сведения о вершинах, ребрах, кольцах и прочих элементах. Для объемных тел такой под-