Следовательно,

х' = дгсовф-г/зтф + Х,. = acos8cos<p-6sin0sin(p + Хс; у' =xsin(p + ycosq + Yc = acosOsin<p +AsinOcoscp + y,.; z =0 (0<е<2л).

6.2.3. Гипербола

Известно, что неявное уравнение гиперболы (рис. 6.1) имеет следующий вид:

(6.6)

2 2 X У

-- = 1.

2 Ь2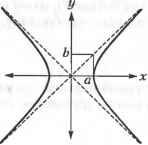

Рис. 6.1. Гипербола

Уравнение (6.6) может быть записано в параметрической форме1:

х = a ch и;

y = bshu. (6.7)

Здесь используется известное тождество ch2 и - sh2 и = 1. Диапазон значений параметра и для уравнения (6.7) определяется исходя из координат конечных точек описываемой гиперболы. Применение соответствующих матриц преобразований к уравнению (6.7) позволяет получить уравнение гиперболы с центром в любой точке пространства, ориентированной произвольным образом.

6.2.4. Парабола

Парабола, симметричная относительно оси х и проходящая через начало координат, может быть задана следующим явным уравнением:

х = су2. (6.8)

Это уравнение может быть преобразовано к параметрическому виду:

х = си2; у =м.

(6.9)

Напомним, что chw =(е + e- )/2 и shu =(е - е'и)/2. Из уравнения (6.6) можно получить и другие параметрические уравнения.

Заметьте, что параметрическое уравнение (6.9) не является уникальным по отношению к уравнению 6.8): вы можете выбрать любое удобное параметрическое уравнение. Диапазон значений параметра и в уравнении (6.9) выбирается исходя из координат концов описываемой параболы. Уравнение произвольной параболы с произвольными координатами центра и ориентацией может быть получено применением соответствующих матриц преобразований к уравнению (6.9).

6.3. Эрмитовы кривые

Чаще всего для описания кривых, используемых в программах CAD, используются уравнения третьего порядка, потому что они обладают важным свойством: две кривые, описываемые такими уравнениями, могут быть соединены таким образом, что вторые производные в точке соединения будут равны друг другу. Это означает, что кривизна в точке соединения остается постоянной, отчего две кривые кажутся одним целым. Ту же непрерывность можно получить и для кривых более высоких порядков, однако работа с ними требует интенсивных вычислений.

Простейшее параметрическое уравнение третьего порядка выглядит следующим образом:

Р(и) = [ф) у(и) z(w)] = (610

= а0 + atu + a2w2 + а3и3 (0<м<1). В формуле (6.10) ао, а а2, а3 - векторные коэффициенты параметрического уравнения, то есть векторы-строки с компонентами х, у и г1. Эти коэффициенты являются обычными алгебраическими коэффициентами2 уравнения, поэтому их изменение не приводит к интуитивно понятному изменению формы кривой.

Чтобы преодолеть этот недостаток алгебраических коэффициентов, мы заменим их векторами, обладающими конкретным геометрическим значением. Один из возможных вариантов - использование радиус-векторов конечных точек кривой Р0 и Plf а также векторов Р'0 и Р[, задающих направление касательных в этих точках. Добавление граничных условий в виде векторов Р0, Pi, Р'0, Р, к формуле (6.10) дает:

Р0 =Р(0) = а0;

Р, =Р(1) = а0+а, +а2+а3; (6 И)

Р; =Р'(0) = а,;

р; =p(i) = ai +2а2 +3а3.

Уравнения (6.11) могут быть решены относительно a а(, а2, а3:

1 Координаты точки мы представляли вектором-столбцом, следуя соглашениям, принятым создателями OpenGL. Здесь же мы используем векторы-строки, потому что это делает более удобным представление матрицы геометрических коэффициентов, приведенной на рис. 6.2.

2 Уравнение (6.10) называется, соответственно, алгебраическим уравнением.

а, =К.

а2 = -ЗР0+ЗР, -2Pj-PJ;

а3 =2Р0-2Р, +р;+р;.

Подстановка (6.12) в (6.10) даст нам уравнение кривой в новом виде:

(6.12)

Р(м) = [1-3ы2+2и3 Зи2-2и3 и-2и2+и3 -и2 + и3]

(6.13)

Теперь в уравнение кривой уже не входят алгебраические коэффициенты - вместо них стоят векторы Р0, Р Р^, Р,. Новые векторные коэффициенты называются геометрическими {geometric coefficients), а уравнение (6.13) называется уравнением эрмитовой кривой (Hermite curve)1. Преимущество эрмитовой кривой в том, что изменение ее формы может быть интуитивно предсказано по изменению геометрических коэффициентов. Например, изменение Р0 или Р, вызовет такое изменение кривой, что ее концы переместятся в новое положение, задаваемое измененными векторами Р0 и Р,. Точно так же изменение Р'0 или Р/ приведет к тому, что касательные к кривой на ее концах станут совпадать с новыми векторами Р^ и Р[ (рис. 6.2).

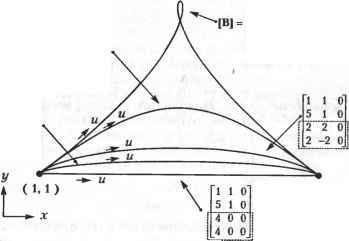
(5,1)

Рис. 6.2. Влияние касательных на форму кривой

Матрица геометрических коэффициентов обозначается буквой [В] и включает векторы Р0, Р„ Р;, Р;. Каждый вектор записывается в своей строке, в той последовательности, в которой они перечислены выше. Рисунок демонстрирует толь-

Эрмитова кривая определяется четырьмя векторами, поэтому они вводятся при ее создании и сохраняются в качестве задающих ее параметров.

ко влияние изменения векторов, определяющих направление и длину касательных. Обратите внимание на то, что происходит с кривой, если меняется только длина, но не направление вектора касательной. Можно заключить, что длина вектора определяет, насколько далеко вдоль кривой по направлению к ее середине распространяется влияние этого вектора.

Формулу (6.13) можно интерпретировать и так, как это сделано ниже. Векторы Р0, Р(, Р'0, Р, влияют на форму кривой, причем относительная степень их влияния определяется функциями

f(u) = \-3u2 + 2и3;

f2(u) = 3u2 -2и3; (614)

f3(u) = u-2u2 -и3; ft(u) = -u2 +и\

Можно сказать, что эти функции сопрягают граничные условия Р0, Pi, Рц, Р[ друг с другом, поэтому и называют их функциями сопряжения (blending functions).

6.4. Кривая Безье

Хотя преобразование алгебраического уравнения кривой в форму эрмитова уравнения позволяет работать с кривой на интуитивном уровне, эрмитова форма не полностью удовлетворяет требованиям разработчикам. Как мы показали, предсказать форму кривой по величине векторов касательных Р'0 и Р, не так-то просто (рис. 6.2).

В начале 60-х гг. Безье - сотрудник французской автомобильной компании Рено - предложил новую форму уравнения кривой и использовал ее в системе поверхностного моделирования UNISURF [19]. Эта кривая получила название кривой Безье (Bezier curve). Она строится по вершинам многоугольника, заключающего ее в себе. Вершины сопрягаются соответствующими функциями подобно тому, как это делается при построении эрмитовой кривой. Безье выбрал функции сопряжения таким образом, чтобы получающаяся кривая удовлетворяла следующим требованиям.

□ Кривая проходит через первую и последнюю вершины многоугольника.

□ Направление вектора касательной в первой точке кривой совпадает с направлением первого отрезка многоугольника (рис. 6.3). Аналогичным образом, последний отрезок многоугольника определяет направление касательной в конечной точке кривой.

□ Производная степени п в начальной (или конечной) точке кривой определяется положением первых (или последних) п + 1 вершин многоугольника. Это свойство очень удобно при соединении двух кривых Безье, если требуется удовлетворить требованию непрерывности высших производных в точке соединения. Вообще говоря, второе свойство есть частный случай данного свойства.

□ При изменении порядка вершин многоугольника на противоположный получается та же самая кривая.

Задавшись этими требованиями, Безье выбрал в качестве функций сопряжения полином Бернштейна:

где

В,.Ли)=\ .\и'(1 -и)-\

(6.15)

i\(n-i)\

Если функцию сопряжения (6.15) применить к вершинам многоугольника, получается уравнение кривой Безье:

Р(и) = £

(6.16)

где Р, - радиус-вектор 2-й вершины. Вершины многоугольника называются задающими (control vertices), как и сам многоугольник (control polygon). Из формулы (6.16) видно, что для кривой, заданной п + 1 точками, максимальная степень будет и . Таким образом, степень кривой Безье определяется количеством задающих точек. Кривые Безье разных степеней с разным количеством задающих точек показаны на рис. 6.3.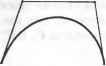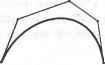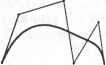

а б в

Рис. 6.3. Кривые Безье различных степеней

Покажем теперь, что кривая Безье, заданная уравнением (6.16), удовлетворяет требованиям, перечисленным в начале раздела. Для начала проверим, что кривая проходит через первую и последнюю задающие точки. В этом легко убедиться, подставив в уравнение значения 0 и 1 параметра и. Раскроем суммирование следующим образом:

Р(и) =

(1-и) Р0 +

м2(1- Г2Р2 +

и-1 (1-й)+

{п-1)

Рассчитаем значения Р(0) и Р(1):

р = Р

Мы убедились, что кривая проходит через первую и последнюю задающие точки. Второе и третье свойства можно проверить дифференцированием уравнения кривой Безье, чем мы займемся в следующем разделе. Четвертое свойство проверяется путем рассмотрения двух кривых, определяемых уравнениями

P( ) = if V(l- rP, (0<и<1); (6.17)

P(v) = Zyv41-v)n>Q, (Q, =P .j, 0 <v<l). (6.18)

Уравнения (6.17) и (6.18) можно интерпретировать следующим образом: кривая Р(и) проводится от точки Р0 к точке Р„, тогда как P*(v) проводится от P (=Qo) к Ро(=Ол)- Если мы введем новый параметр и и заменим v на (1 - и), направление Р* изменится на противоположное (то есть кривая будет идти от Р0 к Р„ при изменении и от 0 до 1). Поэтому мы сможем сказать, что кривые Р и Р* идентичны, если Р*(1 - и) при разложении даст нам то же выражение, что и Р(и) с точностью до названий параметров. Мы получим выражение для Р*(1 - и), подставив (1 - и) вместо v в формулу (6.18).

<>- >-1( )

Перепишем выражение (6.19), подставив в него г вместо (п - j):

р-<1- >=£(

= Х

п

Поскольку

эквивалентно

п-г

и) -1и'Р, = и)п-1и%.

(6.19)

(6.20)

п

мы можем заключить, что формула (6.20) совпадает с (6.17). Кривая Безье обладает еще одним важным свойством, помимо перечисленных выше, - выпуклостью оболочки (convex hull property). Выпуклой оболочкой кривой Безье является выпуклый многоугольник, получаемый соединением задающих точек (рис. 6.4). Обратите внимание, что на этом рисунке все кривые Безье полностью лежат внутри своих выпуклых оболочек.

Выпуклость оболочки кривой Безье обеспечивается тем, что значения сопрягающих функций лежат на отрезке [0,1], а их сумма равна 1 для любого и. Это утверждение легко проверить для кривой Безье, определяемой двумя задающими точками. Кривая, заданная точками Р0 и Р будет отрезком прямой, а ее выпуклой оболочкой будет тот же самый отрезок. Любую точку этой кривой можно полу-

чить сложением Po#o.i + Л^и- Поскольку функции сопряжения В0, и В положительны и их сумма равна единице для любого и, точка, определяемая выражением PqBi + P-Bi,i, будет лежать на отрезке Р0Р, и делить его в отношении BiЛ:В()д. Отрезок PqPi в нашем случае представляет собой вырожденную выпуклую оболочку, поэтому мы можем сказать, что все точки кривой лежат внутри этой оболочки. Аналогичным образом можно проверить высказанное выше утверждение для кривой Безье, заданной тремя и более точками, как показал Фа-рин [48]. Выпуклость оболочки полезно использовать при вычислении точек пересечения кривых Безье. Оболочка кривой содержит ее целиком, поэтому кривые Безье не могут пересекаться, если не перекрываются их оболочки. В этом случае трудоемкое вычисление точки пересечения кривых Безье можно сразу же пропустить. Проверка перекрытия выпуклых оболочек требует гораздо меньших вычислительных затрат.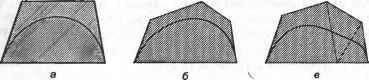

Рис. 6.4. Примеры выпуклых оболочек

6.4.1. Дифференцирование уравнения кривой Безье

Часто приходится вычислять не только значения координат точек, лежащих на кривой, но и значения первой производной, а также и производных более высокого порядка. Например, производные первого и второго порядка могут потребоваться для определения кривизны кривой. Производная первого порядка необходима также для вычисления точки пересечения кривых по итерационному методу Ньютона- Рафсона1 [39].

В этом разделе мы получим выражение для производных кривой Безье. Эти выражения показывают соотношения между производными кривой и задающими ее точками. Перепишем выражение (6.16) в виде

P( ) = lf ) ,(i- rP,.

Продифференцируем выражение по параметру и10:

- X( V~(i- r,pi -2>-of*V(1- >n~Mp. = <6-21)

=! V V i-0

n-l ( г) \ и-1

= Ю'+1> . , k(i- r-;-P;+1 -i(n-i) . U(i- rwp,

Метод расчета точек пересечения кривых излагается в разделе 6.8.

Множители

0 + 1)

J+1)

(и-О

в формуле (6.21) могут быть расписаны в явном виде следующим образом:

0+1)и! п(п-\)\

0 + 1)

U + 1; (я-О

0 + 1)!(г2->-1)! JKn-j-\)\

(n-i)n\ n(n-i)\ Jn~i\ ~ tl(n-t)l ~ !(и-г-1)! I i )

n-l]

Подстановка (6.22) и (6.23) в (6.21) дает:

dP(u)

u>(i-U)v,p;+i -nfn .x it/(i- rMPi

72-1

(n-l

= nn - ) (P,+,-P,)-i=o V * )

Заменив Pi+i-P на a выразим формулу (6.24) в виде dP(us

du U\ г J

(6.24)

(6.25)

Правая часть формулы (6.25), если забыть о множителе п, стоящем перед знаком суммирования, представляет собой уравнение кривой Безье, заданной точками а0, a,.....а„ ,. Отсюда получаем следующие равенства:

ti{ г

и'а-иГ-а,

ы'(1- Г, а,

(6.26)

(6.27)

Равенства (6.26) и (6.27) выражают тот факт, что кривая Безье проходит через первую и последнюю задающие точки. Из формул (6.25), (6.26) и (6.27) можно получить значения первой производной в начальной и конечной точках:

= иа0 =n(Pl -P0);

= лав , = n(Pn-Pn ,).

(6.28)

(6.29)

Поэтому можно утверждать, что касательные к кривой Безье в ее начальной и конечной точках совпадают по направлению с первым и последним отрезками задающего многоугольника. Кроме того, формула (6.25) может использоваться

для рекурсивного определения производных более высоких порядков, поскольку ее правая часть совпадает по форме с уравнением кривой Безье. Отсюда выражение для второй производной имеет вид

* = п{п-\)±[П^\\\-иу-*-%, (6.30)

dul ый\ г J

где b, = а1+1 - а,. Выражение (6.30) говорит нам, что вторая производная в начальной точке определяется векторами Р„, Р„ Р2, а в конечной точке - векторами

Р/?-2 Рл-I Р -

Продолжая дифференцировать уравнение (6.30), мы будем тем же путем получать уравнения для производных более высоких порядков. Таким образом, мы можем показать, что производные порядка г в начальной и конечной точках определяются координатами г + 1 задающих точек.

6.4.2. Вычисление кривой Безье

Даже если у нас есть формула, описывающая кривую, например уравнение кривой Безье, это уравнение будет практически бесполезным, если мы не найдем эффективного способа вычислять координаты точек на кривой. Мы знаем, что для отображения кривой необходимо вычислять координаты точек с небольшим приращением параметра, и делать это достаточно эффективно. Посмотрев на уравнение кривой Безье (6.15), можно прийти к выводу, что нам придется достаточно часто вычислять биномиальный коэффициент

в функции сопряжения Bin(u), а это требует серьезных затрат. Поэтому нам может понадобиться алгоритм, позволяющий вычислить точку на кривой Безье непосредственно, без вычисления значений биномиальных коэффициентов. Такой алгоритм существует и называется алгоритмом де Кастилъо (de Casteljau algorithm). Он излагается в приложении Е.

6.5. В-сплайн

Вспомните, что степень кривой Безье определяется количеством задающих точек, причем все они влияют на форму всей кривой. Эти особенности кривых Безье создают определенные неудобства. Во-первых, при аппроксимации кривой сложной формы при помощи кривой Безье неизбежно используется множество задающих точек, в результате чего получается кривая высокого порядка. Такая кривая может осциллировать, но она к тому же создает большую вычислительную нагрузку на компьютер. Почему бы в таком случае не попытаться представить ту же исходную кривую множеством кривых Безье низших порядков, чтобы избежать этих неприятностей? Проблема в том, что соединение кривых с обеспечением непрерывности производных нужных порядков оказывается довольно сложной процедурой.

Во-вторых, трудоемким оказывается локальное изменение формы кривой. Кажется естественным переместить задающие точки вблизи изменяемого участка кривой, и действительно, это приводит к модификации нужной области, но вместе с ней изменяется вся кривая целиком. Эта особенность называется свойством

глобальности изменений (global modification property). Глобальность изменений нежелательна при создании кривых заданной формы, поскольку кривые всегда создаются или проектируются путем непрерывной модификации грубой формы начального приближения. В системах автоматизированного проектирования желательно наличие прямо противоположного свойства - локальности изменений (local modification property).

Описанные недостатки кривых Безье связаны с выбором функций сопряжения. Таким образом, нам нужно выбрать новый набор функций сопряжения, обладающих определенными свойствами. Во-первых, в определение новой функции сопряжения не должно входить число точек п, в отличие от функции Bin(u). Степень функции сопряжения, а значит, и степень кривой, должны быть независимы от числа задающих точек п. Во-вторых, все функции сопряжения должны быть отличны от нуля только на ограниченных подмножествах значений параметра, причем для каждой функции такое подмножество должно быть уникальным. В этом случае форма сегмента будет определяться только теми задающими точками, которые учитываются функциями сопряжения, имеющими ненулевые значения на данном сегменте.

В 1972 г. Кокс [41] и де Бур [43] предложили использовать функции Nu), определяемые рекурсивно. Кривая, которая строится таким образом, называется В-сплайном (B-spline) и записывается в следующем виде:

Р(и) = IP,JV, (fH <и < tk+l ), (6.31)

где

(ц)(ц~*)АГ*(ц) i (fr+t-M+u-ifr). (6.32)

.( ) = {1 (6.33)

[0 в противном случае.

Значения называются узловыми - они ограничивают отрезки значений параметра, внутри которых функции сопряжения имеют ненулевые значения . В формуле (6.32) неопределенность 0/0 считается равной нулю. Как следует из этого уравнения, для определения п + 1 функций сопряжения необходимо задать п + k + 1 узловых значений от t0 до tn+k. Разные методы задания узловых значений позволяют получить разные функции сопряжения и, соответственно, разные кривые. Ниже мы расскажем, как это делается. Обратите внимание, что из формулы (6.32) следует, что одновременный сдвиг всех узловых значений на одно и то же число не приводит к изменению формы кривой. При этом происходит лишь изменение диапазона значений параметра для уравнения (6.31). Проверим, удовлетворяют ли функции сопряжения, заданные уравнениями (6.32) и (6.33), требованиям, изложенным в начале раздела. Из уравнения (6.32) следу-

1 Когда и совпадает с границей интервала, следует быть аккуратным, поскольку для любого значения и только одна функция Nu(u) может быть отличной от нуля. Это предполагается в определении (6.32). Например, когда и - tu только одна из функций N0,i(ti) и /V, i(ri) может быть равна единице, хотя из уравнения (6.33) следует, что они обе могли бы иметь это значение. В любом случае значение P(fi) окажется одним и тем же.

ет, что степень NiJt(u) на единицу выше, чем у Nji(u) и Ni+,k i(u). Следовательно, Ni2(u) имеет степень 1, поскольку NiA(u) - константа, a Ni3(u) по той же причине имеет степень 2. Продолжая в том же духе, можно прийти к выводу, что функция NiJt(u) имеет степень к - 1. Таким образом, степень В-сплайна определяется не числом задающих точек, а значением к, которое должно быть на единицу больше желаемого значения степени кривой. Значение к называется порядком В-сплайна (order of the B-spline curve).

Чтобы показать, что любой участок В-сплайна определяется лишь конечным числом задающих точек, рассмотрим сегмент кривой, соответствующий значениям параметра из отрезка [th ti+l]. Влиять на этот сегмент будут те задающие точки, функции сопряжения которых (порядка к) отличны от нуля на отрезке [tit ti+i]. Среди функций первого порядка от нуля отлична только NiA(u). Подставив Nit(u) в правую часть формулы (6.32), мы получим ненулевые на рассматриваемом отрезке функции Nj2(u) и Nj i2(u). Первая функция получается подстановкой Nti(u) в первое слагаемое, а вторая функция - подстановкой во второе слагаемое. Затем по ненулевым функциям N,2(u) и Nj i2(u) мы получаем функции третьего порядка и т. д., пока не будут получены функции порядка к. Распространение ненулевых значений иллюстрирует рис. 6.5.

. Ni-k+i,k

Ni-k+2,k-l Ni-k+2.k

Ni-2,3

/ / / /

Щ\ -- ЛЬ. . . -* Niik-i Niik

Рис. 6.5. Распространение значений Nfi1(u)

По рис. 6.5 видно, что ненулевые значения на отрезке [t будут иметь только

функции Nj k+lJt, Л^ £+2*.....JV. Поэтому и влиять на форму отрезка кривой будут

только точки P, i+i, P, i+2i -i Pi (всего к штук). Например, если взять кривую четвертого порядка, то на форму отрезка будут влиять четыре задающие точки, а все остальные не будут.

Займемся теперь определением п + к + 1 узловых значений от to до t +k. Узлы бывают двух основных типов: периодические и непериодические. Периодические узлы определяются из равенства

t, =i-k (0<i<n + k). (6.34)

Непериодические узлы задаются формулой

О 0 < i < k;

t, = i-k + i k<i<n; (6.35)

n-k + 2 n <i <n + k.

Главное отличие узлов разных типов состоит в том, что первый и последний непериодические узлы повторяются к раз. Повторение узлов приводит к тому, что В-сплайн проходит через первую и последнюю задающие точки подобно кривой Безье. В периодическом В-сплайне первая и последняя точки влияют на форму кривой точно в той же степени, что и все остальные точки, а потому кривая не проходит через них. Вообще говоря, функция сопряжения для периодических узлов повторяется через равные промежутки значений параметра, почему узлы и называются периодическими. Непериодические кривые чаще используются в системах автоматизированного проектирования, поскольку большинству конструкторов привычнее работать с кривыми, проходящими через первую и последнюю точки.

Выражения (6.34) и (6.35) показывают, что расстояние между соседними узлами всегда одинаково и равно единице. Такие узлы называются однородными (uniform knots), как и В-сплайн, через них проходящий. Однородный В-сплайн может быть как периодическим, так и непериодическим. При изменении формы кривой конструкторы часто добавляют1 и удаляют узлы, в результате чего В-сплайн становится неоднородным. Поскольку однородность является частным случаем неоднородности, неоднородные В-сплайны считаются обобщением однородных. Таким образом, большинство САПР позволяют создавать и модифицировать неоднородные и непериодические В-сплайны.

Приведенные ниже примеры должны прояснить суть описываемых в этом разделе понятий.

Пример 6.3

Записать уравнение непериодичного однородного В-сплайна третьего порядка в полиномиальной форме. Задающие точки кривой: Р0, Pi и Р2.

Решение

По формуле (6.35) узлы t, имеют следующие значения:

t0 =0, tt =0, t2 =0, t3 = 1, г4 =1, t5 =1.

Параметр и меняется от 0 до 1. Воспользуемся формулой (6.33), чтобы получить функции сопряжения первого порядка - Nit(u):

0,; случае; [1 £, <и <t2 (и =0); [О в противном случае; [1 t2 < и < t3 (и < 1); [О в противном случае;

JV01(w) = i

[0 в противном с

N2A(u) =

1 При создании поверхности из набора В-сплайнов необходимо, чтобы узловые значения всех кривых были одинаковыми. Подробно об этом рассказывается в работе Тилле-ра [152].

*<-и£Аи

[О в противном с. [у) в противном с.

= 1);

случае;

= 1);

случае.

Мы должны выбрать, какая из трех функций N0A(u), NiA(u) и N2A(u) будет иметь ненулевое значение при и = 0. Пусть это будет функция N2A(u). Аналогично, выберем ту же функцию N2A(u) в качестве ненулевой в точке и = 1. Таким образом, N2A(u) становится единственной ненулевой функцией сопряжения первого порядка для диапазона значений параметра [0,1], причем на всем этом диапазоне она постоянна и равна единице.

Теперь получим нетривиальные функции сопряжения второго порядка по формуле (6.32)1:

N u(;>=m + - ). d-u = (1 и);

Л/ 2;Аи) =-+-=--

t3 - £2 £4 -13 1

Аналогичным образом получим функции сопряжения третьего порядка:

= ы(1-и) + (1-ы)и = 2м(1-и);

Итак, раскрытое в полиномиальной форме уравнение В-сплайна имеет вид:

Р(и) = (1-и)2Р0 + 2и(1-и)Р1 + ы2Р2. (6.36)

Уравнение кривой Безье с задающими точками Р0, Pj и Р2 тоже можно записать в полиномиальной форме:

Р(м) = (о) °<1- >2po+(i) а-УР,

2J2 2(1- >°P (6.37) = (1-ы)2Р0+2и(1-ы)Р, +ы2Р2. Сравнивая формулы (6.36) и (6.37), можно прийти к выводу, что непериодический однородный В-сплайн третьего порядка с задающими точками Р0, Р, и Р2 совпадает с кривой Безье, определяемой теми же задающими точками. Верно и более общее утверждение: непериодический однородный В-сплайн совпадает с кривой Безье с теми же задающими точками, если порядок k совпадает с количеством задающих точек п + 1. Другими словами, кривая Безье представляет собой частный случай В-сплайна.

1 г>

вьфажении для Nl2(u) первый член с Nu равен нулю, поскольку он представляет собой неопределенность вида 0/0.

Пример 6.4

Записать уравнение непериодичного однородного В-сплайна третьего порядка с задающими точками Р0, Р„ --, Р5 в полиномиальной форме и продемонстрировать свойство локальности изменений.

Решение

По формуле (6.35) определяем узловые значения t;.

t0 =0, tt =0, r2 =0, s=l, tt =2, t5 =3, tb = 4, r7 =4, rs =4. Параметр и меняется от 0 до 4. Воспользуемся формулой (6.33) для получения функций сопряжения первого порядка - NiA(u):

1 0<ы<1;

[0 в противном случае; 1 1<м<2;

[0 в противном случае; 1 2<и<3;

[0 в противном случае; 1 3<w<4;

10 в противном случае.

N2A(u)--N3A(u)--

JV5..( ):

Функции N0 ,(ы) и JV, i(w) мы не рассматриваем, выбирая N2A(u) в качестве единственной отличной от нуля при и = 0. По той же причине не рассматриваются Nc ,(ы) и N7,( ). Теперь вычислим нетривиальные функции сопряжения второго порядка по формуле (6.32):

t2 - tl t3 t2

XJ , ч ( -t2)N2A . (tt -u)N3A N2a(u) = -

t3 t2

±-=uN2A +(2-u)N3A;

N32(u)JU-N3l+it5~U)Nii =(u-l)N3A +Q-u)Nui

h-t, t0-t5

te -h

Аналогичным образом вычисляются функции сопряжения третьего порядка:

AW=( 7to) °2 +{t\-u)Nl* -Q-u)N =d- )2N ;

t2 t0

t3 -tt

, ч (M-tt)Nu (t4-n)A/M 2-й

N,3(u) =-+ -;----WJVi,2 + n

t3 -tt th -t2 2

W2.2 =

Глава 6. Представление кривых и работа с ними

t4 t2

2 2Л

2 2.2 --J-

ц(2-ц) (3-м)(ц-1) 2 2

t5 t3

( -l)2

(а-П(З-ц) (4-ц)(ц-2)

v4.sW--;-;-+ -:--=-N42 +(4-u)N5

(u-2)2

r7 -t, 2

(1/-2)(4-ц)

+ (4-и)(м-3)

(M-t5)Ar (гв-ц)ДГ --:-:- + -:-:-=(

*7 ~t5

t-8 t-6

3)N,2=(M-3)2JV51.

Таким образом, уравнение В-сплайна в раскрытой полиномиальной форме ет вид:

Р(и)=(1-и)2ЛГ2ЛР0 +

и(\-и) +

N2A +V-pN

( -1)2 jy , Г(и-1ХЗ-и) , (4-ы)(ц-2) 2 >.+ L 2-+-j-

+( -3)2JV5,P5.

(м-2Х4-И)

+ (4-ы)(м-3)

5, P. +

Форма выражения (6.38) заставляет предположить, что любая задающая точка влияет на форму всей кривой. Однако если записать это уравнение отдельно для каждого отрезка значений параметра и, станет видно, что на каждый сегмент влияет лишь ограниченное подмножество задающих точек всей кривой. Рассмотрим отрезок 0 u 1. Пусть Pi(w) обозначает уравнение соответствующего участка кривой (то есть первого ее сегмента). Для значений параметра и от 0 до 1 только одна функция первого порядка будет отлична от нуля и равна единице - Nu-Поэтому формулу (6.38) на этом отрезке можно записать следующим образом:

6.5. в-сплайн

Р,(ц) = (1-Ц)2Р0+ ц(1-ц) + (2 UaU Р, +уР2 (0<и<1). (6.39)

Аналогичным образом можно получить Р2(и) для отрезка 1 и 2, оставив только те слагаемые, в которые входит N3l(u):

ы(2-ы) + (3-ы)(ы-1)

Р2+-Р3 (1<и<2). (6.40)

Тем же способом получим и запишем выражения для участков P3(w) и Р4(г/), со ответствующих отрезкам значений параметра 2 и 3 и 3 и 4.

Рз( ) = Р<( ) =

(3-ц)г 2

(4-и)2

Р2 +-(-2м2 +10и-11)Р3 +

(и-2)2

р<;

Р3 +-(-Зм2 + 20ы-32)Р4 + (ы-3)2Р5.

(6.41)

(6.42)

Присваивая нужные значения задающим точкам Р0, Pi,..., Р5, мы можем нарисовать все сегменты В-сплайна по формулам (6.39)-(6.42). Один из возможных подходов продемонстрирован на рис. 6.6. Обратите внимание на важные особенности В-сплайнов, проявляющиеся на рис. 6.6.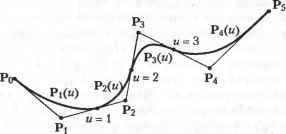

Рис. 6.6. В-сплайн, состоящий из криволинейных сегментов

Любой В-сплайн представляет собой составную кривую, состоящую из нескольких разных кривых (в нашем примере - P((w), Рг( ), Рз(и), Р4(ы)). Эти кривые соединяются в узловых точках параметра. В этом примере в точках соединения выполняются следующие равенства: Р,(1) = Р'2 (1), Р2 (2) = Р3(2) и Р33) = Р4(3). Убедитесь в этом, вычислив производные выражений (6.39)-(6.42). Эти равенства означают непрерывность первой производной в точках соединения сегментов кривой. Тем же методом можно заключить, что непрерывность второй производной в этих точках нарушается. Это следует уже из того, что степень уравнений (6.39)-(6.42) равна 2. Производные В-сплайна непрерывны вплоть до порядка к - 2, потому что степень уравнения каждого сегмента равна к - 1. Например, у В-сплайна четвертого порядка непрерывными в точках касания сегментов будут первая и вторая производные.

На каждый сегмент кривой влияют к задающих точек. Это следует из уравнений (6.39)-(6.42). Первые к задающих точек определяют форму первого сегмента, следующие к (начиная со второй) - форму второго сегмента, и т. д. Последние к точек определяют форму сегмента n-k + 2 (рис. 6.7).

□ Рисунок 6.7 демонстрирует, что одна задающая точка может влиять не более чем на k сегментов. Проверить это утверждение можно, подсчитав количество групп, содержащих, например, точку Рц. Мы заключаем, что каждая точка влияет не более чем на к соседних сегментов. Это и есть свойство локальности изменений.

Ро Pi

P*-i Р*

И .

Р„ * P t+1 Р„ , Р„

Pl( )

Р2( )

Р -*+2(ы)

Рис. 6.7. Задающие точки и сегменты кривой

6.5.1. Вычисление В-сплайна

Как вы могли убедиться, изучив предшествующие примеры, расписать функции сопряжения В-сплайна в полиномиальной форме - задача непростая. Особенно сложной она становится при больших к. Поэтому для вычисления координат точек кривой полиномиальная форма уравнения В-сплайна используется редко. Вместо этого конкретные значения параметра и подставляются в рекуррентное уравнение (6.32) и по ним вычисляются координаты точек, соответствующих этим значениям параметра. Кокс [41] и де Бур [43] предложили переписать уравнение (6.32) таким образом, чтобы вместо рекуррентной подстановки получить итерацию, подобно тому как это делается в алгоритме де Кастильо. Их метод позволяет определить задающие точки В-сплайнов, получающихся при делении исходной кривой в вычисляемой точке (см. приложение Ж).

6.5.2. Объединение В-сплайнов

В-сплайн можно не только разделить на два В-сплайна, но и объединить с другим В-сплайном, в результате чего получится В-сплайн того же порядка. Задача заключается в том, чтобы найти задающие точки и узловые значения для объединенной кривой. Подробное описание этой процедуры заинтересовавшиеся могут найти в приложении 3.

6.5.3. Дифференцирование В-сплайна

Мы уже показали, что производная от кривой Безье выражается через кривую Безье, порядок которой на единицу меньше порядка исходной кривой. Аналогичным образом, производная В-сплайна записывается через уравнение В-сплайна, порядок которого на единицу меньше исходного. Производная от В-сплайна, при условии что параметр и лежит в диапазоне tt и t,+l, имеет следующий вид (доказательство приводится в приложении И):

= ХР.ЧмОА (6.43)

где Р,1 определяется следующим выражением:

р =(*-i)P-p-;. (6.44)

Правая часть уравнения (6.44) имеет форму уравнения В-сплайна, поэтому можно предполагать, что производные более высоких порядков могут быть получены рекурсивным применением формулы (6.43). Так, производная порядка г от В-сплайна имеет вид:

= &[М^г(и), (6.45)

аи i=;-t+r+i

где

рг-1 рг-1

p.=(£ r)fJ-l!=L, (6.46)

Равенство (6.45) выполняется, если и лежит на отрезке Ц и £ж, а функция Р,г в формуле (6.46) определяется, как и ранее, через Р;. Численные значения производных могут быть вычислены по алгоритму Кокса - де Бура, поскольку формулы (6.43) и (6.45) имеют вид уравнения В-сплайна.

Пример 6.5

Вычислить первую производную от В-сплайна в его конечных точках, используя формулы (6.43) и (6.44). Порядок В-сплайна равен к, а его задающие точки Р0, Рп Р -Решение

Начальной точке В-сплайна соответствует значение параметра t0 = tx = ... = 4-i. а нас интересует первый сегмент, которому соответствует отрезок значений параметра tk i и tk. Мы получим значение производной в начальной точке, подставив к - 1 вместо / и 4-1 вместо и в уравнение (6.43):

аи i=i

Выражение в правой части равенства имеет вид уравнения В-сплайна, а значение и = 4 i соответствует начальной точке кривой. Следовательно, сумма UPiijn(*-i )должна быть равна вектору координат первой задающей точки Р,1. Отсюда первая производная исходного В-сплайна в начальной точке име ет значение:

аи tk - г,

Производная на втором конце кривой вычисляется тем же методом. Параметр в конечной точке имеет значение t +l, а интересующему нас сегменту соответствует отрезок значений параметра t и t +l. Подстановка п вместо 1 в уравнение (6.43) дает:

UU Ып-к+2

лава о. i (редставление кривых и раоота с ними

В правой части снова получилось уравнение В-сплайна, а значение и = £ +, соответствует конечной точке кривой. Отсюда, сумма X-jPmCi) совпадает с координатами последней задающей точки Р„. Производная первого порядка от исходной кривой в таком случае имеет следующий вид:

du

В изложенном примере мы продемонстрировали еще одно важное свойство В-сплайна: вектор касательной в начальной или конечной точке совпадает по направлению с первым или последним ребром задающего многоугольника. Для кривых Безье это свойство было доказано еще раньше.

6.6. Неоднородный рациональный В-сплайн

Неоднородный рациональный В-сплайн, или попросту NURBS (nonuniform rational B-spline curve), подобен обычному неоднородному В-сплайну, поскольку основан на тех же функциях сопряжения, получаемых для неоднородных узлов. Однако задающие точки рационального В-сплайна указываются в форме, то есть с использованием однородных координат. Функции сопряжения применяются именно к этим однородным координатам. Координаты точки на кривой NURBS в однородном пространстве получаются по формулам:

*-Ь = J(A,-*,)A/u(m); (6.47)

УЬ = £(Ь,-УЖЛ > (6.48)

;=о

z-h = £(hrz,)Nij,(u): (6.49)

A = 2>Aa( )- (6.50)

Координаты точки в трехмерном пространстве х, у и z получаются делением xh, yh и zh на h, поэтому уравнение кривой NURBS в векторном виде может быть записано следующим образом (здесь мы поделили уравнения (6.47), (6.48) и (6.49) на (6.50)):

£й,Р,.Лии) Р(и) = -, (б-51)

где Р, - вектор (xh уь z,), объединяющий координаты 2-й задающей точки в трехмерном пространстве, как и для нерациональных В-сплайнов. Диапазон значений параметра и tn+i, как и для В-сплайна (см. предыдущий раздел). Уравнение (6.51) отражает следующие свойства кривой NURBS.

□ Подобно нерациональному В-сплайну, кривая NURBS, представленная уравнением (6.51), обязательно проходит через первую и последнюю задающие точки, если используются непериодические узлы. Это утверждение можно

D.D. неоднородный р<дци Hdj ьныи сэ-ишаин

доказать следующим образом. Числитель формулы (6.51) может считаться В-сплайном с задающими точками /г,Р,. Граничным значениям параметра будут соответствовать координаты /?оРо и /г„Р„, поскольку В-сплайн с непериодическими узлами проходит через первую и последнюю задающие точки. Знаменатель (6.51) также может считаться В-сплайиом с задающими точками /г,. Граничным значениям параметра для этого В-сплайна будут соответствовать координаты И0 и h . Следовательно, граничным значениям параметра для Р(и) в целом будут отвечать координаты Р0 и Р„, то есть граничные задающие точки.

□ Касательная в начальной точке совпадает по направлению с вектором Pi - Р0, а касательная в конечной точке - с вектором Р„ - P -i- Проверка этого утверждения приводится в разделе 6.6.2.

□ Знаменатель (6.51) становится равным 1, когда все Л,-е становятся равными 1, поскольку X =oi *( ) = 11 Уравнение (6.51) при этом превращается в уравнение В-сплайна. Поэтому можно сказать, что уравнение NURBS может описывать не только NURBS-кривые, но и обычные В-сплайны. Кривая Безье является частным случаем В-сплайна, поэтому уравнение NURBS может также описывать кривые Безье и рациональные кривые Безье2.

Уравнение NURBS-кривой обладает определенными преимуществами перед уравнением В-сплайна.

□ Форма В-сплайна изменяется при изменении координат х, у и z задающих точек. Для каждой задающей точки, таким образом, имеется три степени свободы. Кривая NURBS позволяет изменять четвертую координату для каждой точки - hi. Появляется возможность работать с кривой на более тонком уровне. Увеличение значения однородной координаты задающей точки приводит к тому, что NURBS-кривая притягивается ближе к этой точке.

□ Уравнение NURBS позволяет точно воспроизвести все конические сечения - окружность, эллипс, параболу и гиперболу. В-сплайны, напротив, допускают лишь приближение к коническим сечениям. Таким образом, в NURBS-пред-ставлении можно работать с коническими сечениями, кривыми Безье, рациональными кривыми Безье и В-сплайнами. Преобразование всех этих кривых к NURBS может значительно сократить объем программирования. Например, можно написать одну-единственную программу для расчета точки пересечения кривых NURBS и использовать ее для расчета пересечений кривых любых типов, поскольку эти кривые всегда могут быть преобразованы к соответствующим NURBS-представлениям.

Продемонстрируем вывод NURBS-представления для конических сечений на примере из книги Пигла и Тиллера [126]. Мы возьмем из этой книги только конечный результат, то есть порядок, координаты задающих точек (однородные) и узловые значения кривой NURBS, эквивалентной дуге окружности. В той же работе обсуждаются NURBS-представления других конических сечений. Дуга ок-

1 Доказательство этого приводится в работе [9].

2 Уравнение рациональной кривой Безье получается подстановкой Д ( ) вместо Nyfc*) в уравнение (6.5 1). Другими словами, функции сопряжения Безье используются с задающими точками в однородных координатах.